9.2.3C Complex Numbers & Equivalent Expressions
Check whether a given complex number is a solution of a quadratic equation by substituting it for the variable and evaluating the expression, using arithmetic with complex numbers.
For example: The complex number $\frac{1+i}{2}$ is a solution of 2x2 - 2x + 1 = 0, since $2\left ( \frac{1+i}{2} \right )^{2}-2\left ( \frac{1+i}{2} \right )+1=i-\left ( 1+i \right )+1=0$.
Apply the properties of positive and negative rational exponents to generate equivalent algebraic expressions, including those involving nth roots.
For example: $\sqrt{2}\times \sqrt{7}=2^{\frac{1}{2}}\times 7^\frac{1}{2}=14^{\frac{1}{2}}=\sqrt{14}$. Rules for computing directly with radicals may also be used: $\sqrt[3]{2}\times \sqrt[3]{x}=\sqrt[3]{2x}$.
Justify steps in generating equivalent expressions by identifying the properties used. Use substitution to check the equality of expressions for some particular values of the variables; recognize that checking with substitution does not guarantee equality of expressions for all values of the variables.
Overview
Standard 9.2.3 Essential Understandings
Generating equivalent expressions and giving reasons as to why two expressions are equivalent provides a cornerstone for making sense of the structure of algebraic expressions. In elementary school students learn multiplication facts by building on facts that they already know. Students who calculate $6\times 8$ by thinking of the problem as $5\times 8+8$ are using the distributive property to reason that both expressions are equivalent. Students who calculate the value of the expression $4\times 7\times 25$ by first multiplying the $4$ and the $25$ to get $100$ then multiply this result by $7$ are using the associative and commutative properties of multiplication to generate equivalent expressions. Instruction at the elementary and middle school levels should pay explicit attention to these properties and how they are used to generate equivalent expressions.
Instruction at the high school should highlight these properties as students begin to work with polynomials. Students need to be able to explain that the expression $(2x+3)(5x+4)$ is equivalent to $10x^{2}+23x+12$ because of the distributive property in much the same way that they used the distributive property to determine that the expression $23\times 54$ is equivalent to $1242$ when they were in elementary school. Students should be able to draw area models to explain how the distributive property works using both numerals and polynomials.
In elementary and middle school students learn to generate equivalent fractions by multiplying by special forms of one. For example, the fraction $\frac{2}{3}$ is equivalent to the expression $\frac{2}{3}\times 1$ which is equivalent to $\frac{2}{3}\times \frac{2}{2}$ which is equivalent to $\frac{4}{6}$. Students at the middle school level should be able to explain the reasons why the expressions are equivalent. At the secondary level students should be able to provide the same reasoning to explain why $\frac{3x(x-2)}{5(x-2)}$ is equivalent to $\frac{3x}{5}$ but this reasoning is more advanced since these two expressions need to be equivalent for all values that the variable can take on. The expression $\frac{3x(x-2)}{5(x-2)}$ is not really equivalent to $\frac{3x}{5}$ since the expression $\frac{3x(x-2)}{5(x-2)}$ is not defined for $x=2$ while the expression $\frac{3x}{5}$ is defined when $x=2$. The two expressions are only equivalent if the domain is restricted to not include $2$.
Students are introduced to radical notation in middle school and are asked to estimate the value of $\sqrt{20}$ to the nearest whole number. Students at the high school are asked to think of these numbers as objects in themselves and to generate equivalent expressions with these new numbers. Some of the properties are the same for these new numbers as they were for rational numbers (e.g. $2\sqrt{3}+5\sqrt{3}$ is equivalent to $7\sqrt{3}$ because of the distributive property just as $\frac{2}{17}+\frac{5}{17}$ is equivalent to $\frac{7}{17}$ for the same reason) while some new properties are introduced that are unique to this new set of numbers (e.g. $\sqrt{20}$ is equivalent to $2\sqrt{5}$ because of the property $\sqrt{a}\cdot\sqrt{b}=\sqrt{a\cdot b}$).
Overall the idea of equivalent expressions has been a focus of the mathematics in grades K to 12. It is very important that students continue to focus on the reasons that make two expressions equivalent rather than memorize isolated sets of rules.
All Standard Benchmarks
9.2.3.1
Evaluate polynomial and rational expressions and expressions containing radicals and absolute values at specified points in their domains.
9.2.3.2
Add, subtract and multiply polynomials; divide a polynomial by a polynomial of equal or lower degree.
9.2.3.3
Factor common monomial factors from polynomials, factor quadratic polynomials, and factor the difference of two squares.
For example: $9x^{6}-x^{4}=(3x^{3}-x^{2})(3x^{3}+x^{2})$.
9.2.3.4
Add, subtract, multiply, divide and simplify algebraic fractions.
For example: $\frac{1}{1-x}+\frac{x}{1+x}$ is equivalent to $\frac{1+2x-x^{2}}{1-x^{2}}$.
9.2.3.5
Check whether a given complex number is a solution of a quadratic equation by substituting it for the variable and evaluating the expression, using arithmetic with complex numbers.
For example: The complex number $\frac{1+i}{2}$ is a solution of $2x^{2}-2x+1=0$, since $2\left ( \frac{1+i}{2}\right ) ^{2}-2\left ( \frac{1+i}{2}\right ) +1=i-(1+i)+1=0$.
9.2.3.6
Apply the properties of positive and negative rational exponents to generate equivalent algebraic expressions, including those involving nth roots.
For example: $\sqrt{2}\times\sqrt{7}=2^{\frac{1}{2}}\times7^{\frac{1}{2}}=14^{\frac{1}{2}}=\sqrt{14}$. Rules for computing directly with radicals may also be used: $\sqrt[3]{2}\times\sqrt[3]{x}=\sqrt[3]{2x}$.
9.2.3.7
Justify steps in generating equivalent expressions by identifying the properties used. Use substitution to check the equality of expressions for some particular values of the variables; recognize that checking with substitution does not guarantee equality of expressions for all values of the variables.
************************************************************************
Benchmark Group C
9.2.3.5
Check whether a given complex number is a solution of a quadratic equation by substituting it for the variable and evaluating the expression, using arithmetic with complex numbers.
For example: The complex number $\frac{1+i}{2}$ is a solution of $2x^{2}-2x+1=0$, since $2\left ( \frac{1+i}{2}\right ) ^{2}-2\left ( \frac{1+i}{2}\right ) +1=i-(1+i)+1=0$.
9.2.3.6
Apply the properties of positive and negative rational exponents to generate equivalent algebraic expressions, including those involving nth roots.
For example: $\sqrt{2}\times\sqrt{7}=2^{\frac{1}{2}}\times7^{\frac{1}{2}}=14^{\frac{1}{2}}=\sqrt{14}$. Rules for computing directly with radicals may also be used: $\sqrt[3]{2}\times\sqrt[3]{x}=\sqrt[3]{2x}$.
9.2.3.7
Justify steps in generating equivalent expressions by identifying the properties used. Use substitution to check the equality of expressions for some particular values of the variables; recognize that checking with substitution does not guarantee equality of expressions for all values of the variables.
What students should know and be able to do [at a mastery level] related to these benchmarks
- Students should know that the imaginary number $i$ is defined as $i^{2}=-1$. They should know that any imaginary number squared equals a negative real number (i.e. $(3i)^{2}=-9$, $(\frac{4}{5}i)^{2}=-\frac{16}{25}$, and $(i\sqrt{5})^{2}=-5$). Furthermore they should know that the principle square root of any negative rational number is an imaginary number (i.e. $\sqrt{-4}=2i$, $\sqrt{-\frac{9}{4}}=\frac{3}{2}i$)
- Students should know that the sum of a real number and an imaginary number equals a complex number.
- Students should be able to add, subtract, multiply, and divide complex numbers to generate equivalent expressions involving complex numbers.
- Students should know that complex numbers arise as a result of solving some quadratic equations. Furthermore they should be able to demonstrate why a complex solution makes the corresponding quadratic equation true using substitution.
- Students should be able to generate equivalent expressions involving radicals using the rule $\sqrt[m]{a}\cdot\sqrt[m]{b}=\sqrt[m]{a\cdot b}$ when $a\geq 0$ and $b\geq 0$.
- Students should know that if $a>0$, then the expression $a^{\frac{m}{n}}$ is defined as being equivalent to the following four expressions: $\left ( a^{\frac{1}{n}}\right )^{m},(a^{m})^{\frac{1}{n}},\sqrt[n]{(a^{m})},(\sqrt[n]{a})^{m}$. Students should know that $8^{\frac{5}{3}}=\left ( 8^{\frac{1}{3}}\right ) ^{5}=(8^{5})^{\frac{1}{3}}=\sqrt[3]{(8^{5})}=\left ( \sqrt[3]{8}\right ) ^{5}$ and select at least one of the identities to explain why $8^{\frac{5}{3}}$ is equivalent to 32.
- Students should be able to generate equivalent expressions involving radicals as well as approximate the value of the expression as a decimal. For example, students should be able to recognize that $\sqrt{20}$ is equivalent to $2\sqrt{5}$ by writing $\sqrt{20}$ as $\sqrt{4}\cdot\sqrt{5}$. They should also be able to use a calculator to approximate both $\sqrt{20}$ and $2\sqrt{5}$ as $4.4721$.
- Students should know how to use the Power Property of Exponents (i.e. $a^{m}\cdot a^{n}=a^{m+n}$), the Quotient Property of Exponents (i.e. $\frac{a^{m}}{a^{n}}=a^{m-n}$), the Power of a Power Property (i.e. $(a^{m})^{n}=a^{mn}$), the Power of a Product Property (i.e. $(a\cdot b)^{n}=a^{n}\cdot b^{n}$), and the Power of a Quotient Property (i.e. $\left (\frac{a}{b}\right ) ^{n}=\frac{a^{n}}{b^{n}}$) when $a>0$ and $b>0$, and $m$ and $n$ can be any real number to generate equivalent expressions.
- Students should know that two expressions are equivalent if they produce equal values when they are evaluated for each number in the domain of the variables used. Furthermore, students need to understand that since all values of the variables must be checked to determine equivalence that this checking by substitution method rarely is adequate.
- Students should be able to use and name properties to explain why two expressions are equivalent.
Work from previous grades that supports this new learning includes:
- In middle students learn that the principle square root of positive squares results in positive whole numbers (i.e. $\sqrt{25}=5$ and $\sqrt{49}=7$) and that the principle square roots of non-perfect squares result in irrational numbers. They should be able to approximate the value of irrational numbers like $\sqrt{7}$ as being between 2 and 3 mentally and also be able to provide an approximate decimal value using a calculator (i.e. $\sqrt{7}\approx 2.54575\cdots$) to a specified place.
- Students in middle school learn to generate equivalent numerical expressions involving positive and negative exponents using the properties of exponents.
- Students know how to evaluate expressions containing integer exponents.
- Students know the definition of equivalent expressions.
NCTM Standards:
(p.296, PSSM) Instructional programs from Pre-K through grade 12 should enable all students to
2.) Represent and analyze mathematical situations and structures using algebraic symbols. In grades 9-12 all students should
- Understand the meaning of equivalent forms of expressions, equations, inequalities, and relations;
- Write equivalent forms of equations, inequalities, and systems of equations and solve them with fluency - mentally or with paper and pencil in simple cases and using technology in all cases;
- Use symbolic algebra to represent and explain mathematical relationships;
- Use a variety of symbolic representations, including recursive and parametric equations, for functions and relations;
- Judge the meaning ,utility, and reasonableness of the results of symbol manipulations, including those carried out by technology.
Common Core State Standards (CCSM)
High School: Algebra
Seeing Structure in Expressions
Interpret the structure of expressions.
· A-SSE.1. Interpret expressions that represent a quantity in terms of its context.
- Interpret parts of an expression, such as terms, factors, and coefficients.
- Interpret complicated expressions by viewing one or more of their parts as a single entity. For example, interpret $P(1+r)^{n}$ as the product of $P$ and a factor not depending on $P$.
· A-SSE.2. Use the structure of an expression to identify ways to rewrite it. For example, see $x^{4}-y^{4}$ as $(x^{2})^{2}-(y^{2})^{2}$, thus recognizing it as a difference of squares that can be factored as $(x^{2}-y^{2})(x^{2}+y^{2})$.
Write expressions in equivalent forms to solve problems.
· A-SSE.3. Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
a. Factor a quadratic expression to reveal the zeros of the function it defines.
b. Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.
c. Use the properties of exponents to transform expressions for exponential functions. For example the expression $1.15^{t}$ can be rewritten as $(1.15^{\frac{1}{12}})^{12t}\approx 1.012^{12t}$ to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
Arithmetic with Polynomials & Rational Expressions
Perform arithmetic operations on polynomials.
· A-APR.1. Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials.
Rewrite rational expressions.
· A-APR.6. Rewrite simple rational expressions in different forms; write a(x)/b(x) in the form q(x) +r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division, or, for the more complicated examples, a computer algebra system.
· A-APR.7. (+) Understand that rational expressions form a system analogous to the rational numbers, closed under addition, subtraction, multiplication, and division by a nonzero rational expression; add, subtract, multiply, and divide rational expressions.
Misconceptions
Student Misconceptions and Common Errors:
- Students mistake $i$ for a variable.
- Students will compute the product of two complex numbers and not write the result as a complex number (i.e. $(2+i)(3-2i)=6-i-2i^{2}$). Although this answer is not wrong, the answer does not emphasize that the set of complex numbers is closed under the operation of multiplication.
- Students will simplify square roots of negative numbers as $\sqrt{-5}=\sqrt{-1}\cdot\sqrt{5}=i\sqrt{5}$. Although this answer is correct the use of the radical notation is not correct. The rule $\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}$ only works when $a\geq0$ and $b\geq0$. This misuse of the property leads to wrong answers when students evaluate expressions like $\sqrt{-3}\cdot\sqrt{-12}=\sqrt{36}=6$. The expression $\sqrt{-3}\cdot\sqrt{-12}$ equals $-6$.
- Students will incorrectly add radical expressions with unlike radicands (i.e. $\sqrt{3}+\sqrt{2}=\sqrt{5}$).
Vignette
In the Classroom
Ms. W is trying to teach her students to add complex numbers. Her students know that $i$ is defined as $i^{2}=-1$ and how that $\sqrt{-9}$ is equivalent to $3i$. In the past she remembers telling her students the rules for adding complex numbers together first then giving them some examples to check if they could follow the rules. She is decides to use a Black Box approach along with a computer algebra system (CAS) to allow them to make and test conjectures for adding complex numbers. The CAS will provide equivalent expressions in simplified form to problems posed by students. A Black Box approach asks students to select problems to enter into the computer and then try to figure out the rules the CAS is using to determine the answer. The goal of the activity is for students to figure out the rules and give reasons as to why the computer is following the rules.
Ms. W: Today we are going to add complex numbers. Before we do this I want you to talk to a partner to talk and find out if you can write an equivalent expression to the following three expressions: $3+5i$ $3i+5i$ $3+5i^{2}$
[After 3 minutes] Andrea: I think the first expression is equivalent to $8i$. You just add the numbers. Ms. W: Do you all agree? Jesse: I do not think you can add anything on the first one. I think the second expression is $8i$ because they are like variables. Ms. W: Is $i$ a variable? Jesse: No, it is the imaginary number. So am I wrong? Ms. W: I am not saying you are wrong, I am asking why do you think you are right. Andrea: I think Jesse is right and I am wrong. You [Ms. W] always make me say that $3x+5x$ is $(3+5)x$ because of the distributive property. If $x$ is just a number then it should be the same as $i$. Jesse: Yeah. $3i+5i$ is the same as $(3+5)i$ because of the distributive property which is equivalent to $8i$. Andrea: But how do use the distributive property for $3+5i$? Bob: I do not think you can do anything. It is like when you have $3+5x$, you just leave the answer as it is. The same is true for $3+5i^{2}$. You just have to leave it. Ms. W: OK. So far we seem to agree that there is nothing you can do to simplify the first and the third expressions but that $3i+5i$ is equivalent to $8i$. Please open up the Wolfram Alpha site and enter in all three expressions and see if you match our current answers. If Wolfram provides another answer, then please try to figure out why. [After 5 minutes.] Ms. W: What did you find? Andrea: We found that we were right about the first two expressions. You can't add unlike terms or use the distributive property unless both terms have the same letter. I am not sure why we got $-2$ for the last expression. You are not supposed to be able to add unlike terms. Bob: We agree with Andrea that we found the correct answers for the first two expressions but now I think I know why $3+5i^{2}$ is equivalent to $-2$. Since $i^{2}=-1$ then $3+5i^{2}$ is equilvanet to $3+-5$ which is $-2$. Ms. W: Good job. Now we are going to try to use Wolfram Alpha to figure out how to add complex numbers. A complex number is like $3+5i$ where you have a real part and an imaginary part. Try to figure out the answers that Wolfram Alpha will give you with these three examples and then try selecting your own examples to figure out how Wolfram Alpha is adding these numbers. Please keep track of any cool patterns you notice.
$(-2+5i)+(5-3i)$ $(-1+5i)+(7i)$ $(2i-3)+(1-4i)$
[After 7 minutes] Sam: This was very easy. We noticed that you are just adding these like we are adding with variables. We know that the imaginary numbers are not variables but the rules are the same. Ms. W: What are the rules? Sam: You just add the real parts to the real parts and the imaginary parts to the imaginary parts. But we noticed something really cool. If you add numbers like $(3+2i)$ to numbers like $(3-2i)$ you could make the imaginary part disappear. Andrea: That is not that cool. Sam: Do you have anything cooler? Andrea: We found that the expression $3+5i^{4}$ is equivalent to $8$, but we do not know why. Ms. W: This is very good. We are going to investigate expressions like this tomorrow. |
Resources
Teacher Notes
- Teachers need to make sure that students think of the expression $5+3i$ as one number with two parts. Students sometimes believe that $5+3i$ is two numbers.
- The set of complex numbers are closed under the operations of addition, subtraction, multiplication, and division. This means that the result of any operation between two complex numbers that is defined will be a complex number. The set of whole numbers is not closed under the operation of subtraction, which resulted in the invention of negative numbers. The set of integers is not closed under the operation of division, which resulted in the invention of rational numbers. Students need to see how this lack of closure resulted in the invention of new numbers. Students need to be able to think of complex numbers as specific numbers and should be able to perform operations that result in complex numbers.
- Students oftentimes believe that two expressions are equivalent if they plug in a number and the results are the same. For example, a student might believe that $2x$ is equivalent to $5x$ since both expression evaluate to $0$ when $x=0$. These two expressions are only equal when $x=0$ and not equivalent when $x$ takes on any non-zero value. Students need to be able to argue how certain properties make expressions equivalent for all values of the variable in to domain.
This activity allows the user to step through plotting a two-variable function, and to judge whether a given starting point is a prisoner or an escapee, in order to understand complex numbers and Julia sets.
A children's book-on-the-Web from Australia, designed to introduce complex numbers in story form in a way that is intuitive and enjoyable for students. John, Betty, and their dog Trevor solve a series of problems designed to introduce integers, fractions, surds, imaginary numbers, complex numbers, Argand diagram; vectors, multiplication in polar form, relating polar and Cartesian form, De Moivre's theorem; and the Mandelbrot set.
This site does an excellent job of explaining what complex numbers are; how to add, subtract, multiply, divide, and simplify complex numbers; and how complex numbers are used to solve and graph quadratic equations with imaginary roots.
Additional Instructional Resources
- Complex Numbers and Matrices
Ch. 2, Complex Numbers and Matrices, in Navigating through Number and Operations in Grades 9-12 (NCTM) provides activities to enable students to demonstrate fluency with addition and multiplication of complex numbers, understand different representations of complex numbers, and to determine the properties of the complex number system and to compare them with other number systems.
Students look for patterns to determine how the calculator adds, subtracts, multiplies and divides complex numbers. In each problem, students examine completed examples and discuss a process with a partner, then complete additional problems to confirm or refine the process.
In this activity, students will substitute numbers from a given list into an expression with a fractional exponent to discover the connection between rational exponents and radicals. As an introduction to rational exponents, students will discover the rule that a fractional exponent is the same as finding a root of a number.
- Imaginary number: a complex number of the form $a\pm bi$ where $b$ does not equal zero and $i$ is the imaginary unit.
- Complex numbers: a number $a+bi$ where $a$ and $b$ are real numbers and $i$ is the imaginary unit (the number $a$ is the real part of the complex number and the number $bi$ is the imaginary part).
- nth root: In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals x. $r^{n}=x$
Reflection - Critical Questions regarding classroom the teaching and learning of these benchmarks
- Do I ask students to explain why two expressions are equivalent or focus on the following of rules.
- Do my students think of expressions like $\sqrt{20}$ and $(3+2i)$ as numbers?
Materials - suggest articles and books
- Weeks, A. (2003). Connecting complex roots to a parabola's graph. On-Math, Volume 1(3).
- Chazen, D. (2008). The shifting landscape of school algebra in the United States. In Algebra and Algebraic Thinking in School Mathematics (70th Yearbook). NCTM: Reston, VA.
- Common Core State Standards
- Ellis, M. W., & Bryson, J. L. (2011). Absolute value equations and inequalities: A conceptual approach. Mathematics Teacher, 104 (8), 592-595.
- Ruddell, M.R., & Shearer, B.A. (2002). "Extraordinary," "tremendous," "exhilarating, "magnificent": Middle school at-risk students become avid word learners with the vocabulary self-collection strategy (VSS). Journal of Adolescent & Adult Literacy, 45, 352-363.
Assessment
Assessment
Example Item 1 Find the values of $a$ and $b$ if $(-2+3i)-(a+bi)=5+5i$.
Source: Made Up Correct Answer: a=-3 and b=-2 Cognitive Level: Understanding |
Example Item 2 Which of the following expressions are equivalent to $\sqrt{-12}\cdot\sqrt{-4}$? A. 36 B. -36 C. 6 D. -6
Source: Made Up Correct Answer: D Cognitive Level: Knowledge |
Example Item 3 What are the solutions to the equation $x^{2}+2x+2=0$? A. $x=0; x=-2$ B. $x=0; x=-2i$ C. $x=-1+i; x=-1-i$ D. $x=-1+2\sqrt{2}; x=-1-2\sqrt{2}$
Source: California Standards Test Released Items - Item 38 Correct Answer: C Cognitive Level: Knowledge |
Differentiation
Extending the Learning
- Students can perform all of the operations involving complex numbers geometrically on the complex plane. There are three complex numbers shown on the complex plane below.
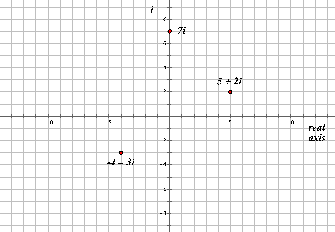
complex plane
Students can add and subtract complex numbers as shown below. This process is similar to operations involving vectors. The picture below shows that the expression $(5+2i)+(3+5i)$ is equivalent to $(9+7i)$.

$(5+2i)+(3+5i)$
Students can make sense of how to generate equivalent expressions when multiplying by a real number like $4(-2+3i)$, which is equivalent to $(-8+12i)$.
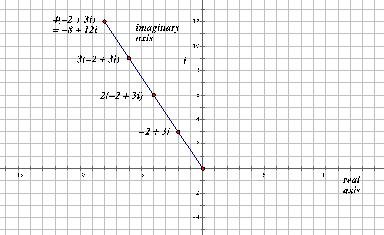
$4(-2+3i)$ is equivalent to $(-8+12i)$
Students can also develop a graphical interpretation of the cyclical nature of multiplying by $i$. Students can be asked to explain the patterns they see as they multiply any complex number by powers of $i$.
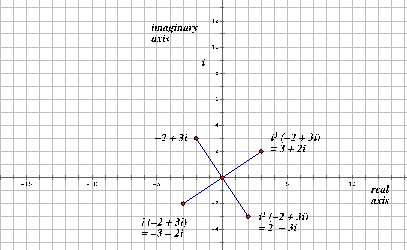
Multiplying any two complex numbers on a complex plane can be done but the use of trigonometry is needed.
- As a coordinating activity, Julia Sets, can be used as an extension.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (make list) | Teachers are: (make list) |
|
|
|
|
|
|
