9.2.3A Polynomials
Evaluate polynomial and rational expressions and expressions containing radicals and absolute values at specified points in their domains.
Add, subtract and multiply polynomials; divide a polynomial by a polynomial of equal or lower degree.
Factor common monomial factors from polynomials, factor quadratic polynomials, and factor the difference of two squares.
For example: 9x6 - x4 = (3x3 - x2)(3x3 + x2).
Overview
Standard 9.2.3 Essential Understanding
Generating equivalent expressions and giving reasons as to why two expressions are equivalent provides a cornerstone for making sense of the structure of algebraic expressions. In elementary school students learn multiplication facts by building on facts that they already know. Students who calculate $6\times 8$ by thinking of the problem as $5\times 8+8$ are using the distributive property to reason that both expressions are equivalent. Students who calculate the value of the expression $4\times 7\times 25$ by first multiplying the $4$ and the $25$ to get $100$ then multiply this result by $7$ are using the associative and commutative properties of multiplication to generate equivalent expressions. Instruction at the elementary and middle school levels should pay explicit attention to these properties and how they are used to generate equivalent expressions.
Instruction at the high school should highlight these properties as students begin to work with polynomials. Students need to be able to explain that the expression $(2x+3)(5x+4)$ is equivalent to $10x^{2}+23x+12$ because of the distributive property in much the same way that they used the distributive property to determine that the expression $23\times 54$ is equivalent to $1242$ when they were in elementary school. Students should be able to draw area models to explain how the distributive property works using both numerals and polynomials.
In elementary and middle school students learn to generate equivalent fractions by multiplying by special forms of one. For example, the fraction $\frac{2}{3}$ is equivalent to the expression $\frac{2}{3}\times 1$ which is equivalent to $\frac{2}{3}\times \frac{2}{2}$ which is equivalent to $\frac{4}{6}$. Students at the middle school level should be able to explain the reasons why the expressions are equivalent. At the secondary level students should be able to provide the same reasoning to explain why $\frac{3x(x-2)}{5(x-2)}$ is equivalent to $\frac{3x}{5}$ but this reasoning is more advanced since these two expressions need to be equivalent for all values that the variable can take on. The expression $\frac{3x(x-2)}{5(x-2)}$ is not really equivalent to $\frac{3x}{5}$ since the expression $\frac{3x(x-2)}{5(x-2)}$ is not defined for $x=2$ while the expression $\frac{3x}{5}$ is defined when $x=2$. The two expressions are only equivalent if the domain is restricted to not include $2$.
Students are introduced to radical notation in middle school and are asked to estimate the value of $\sqrt{20}$ to the nearest whole number. Students at the high school are asked to think of these numbers as objects in themselves and to generate equivalent expressions with these new numbers. Some of the properties are the same for these new numbers as they were for rational numbers (e.g. $2\sqrt{3}+5\sqrt{3}$ is equivalent to $7\sqrt{3}$ because of the distributive property just as $\frac{2}{17}+\frac{5}{17}$ is equivalent to $\frac{7}{17}$ for the same reason) while some new properties are introduced that are unique to this new set of numbers (e.g. $\sqrt{20}$ is equivalent to $2\sqrt{5}$ because of the property $\sqrt{a}\cdot\sqrt{b}=\sqrt{a\cdot b}$).
Overall the idea of equivalent expressions has been a focus of the mathematics in grades K to 12. It is very important that students continue to focus on the reasons that make two expressions equivalent rather than memorize isolated sets of rules.
All Standard Benchmarks
9.2.3.1
Evaluate polynomial and rational expressions and expressions containing radicals and absolute values at specified points in their domains.
9.2.3.2
Add, subtract and multiply polynomials; divide a polynomial by a polynomial of equal or lower degree.
9.2.3.3
Factor common monomial factors from polynomials, factor quadratic polynomials, and factor the difference of two squares.
For example: $9x^{6}-x^{4}=(3x^{3}-x^{2})(3x^{3}+x^{2})$.
9.2.3.4
Add, subtract, multiply, divide and simplify algebraic fractions.
For example: $\frac{1}{1-x}+\frac{x}{1+x}$ is equivalent to $\frac{1+2x-x^{2}}{1-x^{2}}$.
9.2.3.5
Check whether a given complex number is a solution of a quadratic equation by substituting it for the variable and evaluating the expression, using arithmetic with complex numbers.
For example: The complex number $\frac{1+i}{2}$ is a solution of $2x^{2}-2x+1=0$, since $2\left ( \frac{1+i}{2}\right ) ^{2}-2\left ( \frac{1+i}{2}\right ) +1=i-(1+i)+1=0$.
9.2.3.6
Apply the properties of positive and negative rational exponents to generate equivalent algebraic expressions, including those involving nth roots.
For example: $\sqrt{2}\times\sqrt{7}=2^{\frac{1}{2}}\times7^{\frac{1}{2}}=14^{\frac{1}{2}}=\sqrt{14}$. Rules for computing directly with radicals may also be used: $\sqrt[3]{2}\times\sqrt[3]{x}=\sqrt[3]{2x}$.
9.2.3.7
Justify steps in generating equivalent expressions by identifying the properties used. Use substitution to check the equality of expressions for some particular values of the variables; recognize that checking with substitution does not guarantee equality of expressions for all values of the variables.
************************************************************************
Benchmarks Group A
9.2.3.1
Evaluate polynomial and rational expressions and expressions containing radicals and absolute values at specified points in their domains.
9.2.3.2
Add, subtract and multiply polynomials; divide a polynomial by a polynomial of equal or lower degree.
9.2.3.3
Factor common monomial factors from polynomials, factor quadratic polynomials, and factor the difference of two squares.
For example: $9x^{6}-x^{4}=(3x^{3}-x^{2})(3x^{3}+x^{2})$.
What student should know and be able to do [at a mastery level] related to these benchmarks.
- Students should be able to evaluate polynomial or rational expressions using the order of operations using any rational number. For example, students should be able to evaluate expressions like $3x^{3}-2x^{2}+7$ and $\frac{3x}{2x-7}$, when $x=-2$, $x=\frac{2}{3}$, or $x=0$.
- Students should be able to evaluate expressions involving radicals using positive rational numbers or zero. For example, students should be able to evaluate an expression like $\sqrt{2x+3}+5$ for $x=7$ using order of operations and a calculator to calculate the approximate decimal value for $\sqrt{17}$ that is needed in the process of simplifying the expression $\sqrt{2(7)+3}+5$. Students should know how to use a calculator to find decimal approximations for expressions like $\sqrt[3]{-20}$ and $\sqrt[4]{50}$.
- Students should be able to understand the implied grouping symbols to be able to evaluate an expression like $\sqrt{(-3-2)^{2}+(5-3)^{2}}$, $\frac{-3\pm\sqrt{(3)^{2}-4(-2)(10)}}{2(-2)}$ and $\sqrt{1+\sqrt{1+\sqrt{2}}}$.
- Students should be able to evaluate expressions involving absolute values using the order of operations and implied grouping symbols. For example, students should be able to evaluate the expression $3-2\left | 3-2\left ( \frac{3}{4} \right ) \right |$.
- Students should be able to add and subtract polynomial expressions using the associate, commutative, and distributive properties and order of operations to generate equivalent algebraic expressions. Examples include explaining that $(3x^{2}-7x+3)+(2x^{2}+7)$ is equivalent to $5x^{2}-7x+10$ and that $(3w^{3}-7w+5)-(2w^{2}-w-7)$ is equivalent to $3w^{3}-2w^{2}-6w+12$.
- Students should be able to understand the notation that implies multiplication of polynomials and be able to multiply polynomial expressions. For example, students should know that the expression $(2-3b)^{2}$ implies $(2-3b)\cdot(2-3b)$ and be able to use a method to carry out the multiplication to get the equivalent expression $4-12b+9b^{2}$. Students should be able to explain that $4-12b+9b^{2}$ is also equivalent to $9b^{2}-12b+4$.
- Students should be able to recognize that a fraction bar or a division sign ($\div$) can be used to signify the operation of division between two polynomial expressions and be able to use a method to carry out the division. The students should know how the remainder should be written to show equivalence. For example, the expression $\frac{2x^{2}+5x-2}{x-3}$ means $(2x^{2}+5x-2)\div(x-3)$ which is equivalent to the expression $2x+11+\frac{31}{(x-3)}$.
- Students should know that factoring is the re-writing of an expression as a product of two or more factors. They should understand that the process of factoring undoes the operation of multiplication. They should be able to use a method to factor a polynomial expression if possible and know when a polynomial expression is factored completely.
- Students should be able to factor quadratic polynomial expressions like $2x^{2}+6x-20$. They should be able to recognize that $2(x-2)(x+5)$ and $2(x+5)(x-2)$ are both accepted as factored forms of $2x^{2}+6x-20$ and that they are both equivalent to each other as well as the original expression. They should also know that the expression $(2x-4)(x+5)$ is a factored form of $2x^{2}+6x-20$ but it is not factored completely.
- Students should be able to recognize various forms of expressions written as the difference of two squares and factor the expression completely. For example, students should know that the expression $a^{4}-16b^{4}$ is the difference of two squares and can be factored as $(a^{2}+4b^{2})(a^{2}-4b^{2})$. They should also be able to recognize that one of the factors is a difference of squares and that the expression $(a^{2}+4b^{2})(a-2b)(a+2b)$ is an expression that represents the complete factorization of $a^{4}-16b^{4}$.
Work from previous grades that supports this new learning includes:
- Students in middle school learn to use the commutative, associative, and distributive properties and order of operations to generate equivalent expressions involving rational numbers.
- Students in middle school learn how to count a set of objects in different ways as a justification for equivalent expressions.
- Students in middle school should be able to evaluate the principle square root of any positive integer and zero as well as the absolute value of any rational number. The should be able to reason that the value of $\sqrt{20}$ is between 4 and 5 because $\sqrt{16}<\sqrt{20}<\sqrt{25}$.
- Students should be able to explain how place value is used when adding and subtracting multi-digit whole numbers. They should be able to explain that when adding $234+521$ they are adding 2 hundreds and 5 hundreds to get 7 hundreds, 3 tens and 2 tens to get 5 tens, and 4 ones and 1 ones to get 5 ones. Furthermore, they should be able to identify how the commutative, associate, and distributive properties are used to add $2(10)^{2}+3(10)+4$ and $5(10)^{2}+2(10)+1$.
- Students should be able to explain how place value and number properties are used when multiplying two multi-digit whole numbers. They should know that the expression $325+37$ is equivalent to the expression $(3(10)^{2}+2(10)+5)\times (3(10)+7)$ and be able to explain how to use the distributive property to identify all of the partial products.
NCTM Standards:
(p.296, PSSM) Instructional programs from Pre-K through grade 12 should enable all students to
2.) Represent and analyze mathematical situations and structures using algebraic symbols. In grades 9-12 all students should
- Understand the meaning of equivalent forms of expressions, equations, inequalities, and relations;
- Write equivalent forms of equations, inequalities, and systems of equations and solve them with fluency - mentally or with paper and pencil in simple cases and using technology in all cases;
- Use symbolic algebra to represent and explain mathematical relationships;
- Use a variety of symbolic representations, including recursive and parametric equations, for functions and relations;
- Judge the meaning, utility, and reasonableness of the results of symbol manipulations, including those carried out by technology.
Common Core State Standards (CCSM)
High School: Algebra
Seeing Structure in Expressions
Interpret the structure of expressions.
· A-SSE.1. Interpret expressions that represent a quantity in terms of its context.
- Interpret parts of an expression, such as terms, factors, and coefficients.
- Interpret complicated expressions by viewing one or more of their parts as a single entity. For example, interpret $P(1+r)^{n}$ as the product of $P$ and a factor not depending on $P$.
· A-SSE.2. Use the structure of an expression to identify ways to rewrite it. For example, see $x^{4}-y^{4}$ as $(x^{2})^{2}-(y^{2})^{2}$, thus recognizing it as a difference of squares that can be factored as $(x^{2}-y^{2})(x^{2}+y^{2})$.
Write expressions in equivalent forms to solve problems.
· A-SSE.3. Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
a. Factor a quadratic expression to reveal the zeros of the function it defines.
b. Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.
c. Use the properties of exponents to transform expressions for exponential functions. For example the expression $1.15^{t}$ can be rewritten as $(1.15^{\frac{1}{12}})^{12t}\approx 1.012^{12t}$ to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
Arithmetic with Polynomials & Rational Expressions
Perform arithmetic operations on polynomials.
· A-APR.1. Understand that polynomials form a system analogous to the integers, namely, they are closed under the operations of addition, subtraction, and multiplication; add, subtract, and multiply polynomials.
Rewrite rational expressions.
· A-APR.6. Rewrite simple rational expressions in different forms; write a(x)/b(x) in the form q(x) +r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division, or, for the more complicated examples, a computer algebra system.
· A-APR.7. (+) Understand that rational expressions form a system analogous to the rational numbers, closed under addition, subtraction, multiplication, and division by a nonzero rational expression; add, subtract, multiply, and divide rational expressions.
Misconceptions
- Students sometimes do not recognize implied grouping symbols when evaluating expressions involving radicals and fractions. A student who is evaluating the expression $\frac{x-3}{2x+7}$ for $x=5$ might enter in his calculator $5-3/2*5+7$ and get an incorrect answer of $4.5$ rather than entering $(5-3)/(2*5+7)$ and getting the correct answer of $\frac{2}{17}$. Some students incorrectly evaluate the expression $\sqrt{2x}+3$ for $x=8$ as $\sqrt{2*8+3}$ and get the incorrect result $\sqrt{19}$ rather than the correct answer of 7.
- Students will incorrectly add terms that are not like terms (i.e. $2a+3b=5ab$ or $2x^{2}+5x=7x^{3}$).
- Students incorrectly subtract polynomial expressions as shown below:
$(3x^{2}-5x+7)-(x^{2}-3x-2)$
$3x^{2}-5x+7-x^{2}-3x-2$ (not an equivalent expression)
$2x^{2}-8x+5$
- Students will neglect partial products when multiplying polynomials. For example, some students incorrectly simplify the expression $(x-3)^{2}$ by writing $(x)^{2}+(-3)^{2}$ and ending up with $x^{2}+9$ for an answer. Some students incorrectly apply a memorized "FOIL" procedure when simplifying expressions like $(x^{2}-3x+9)(x+2)$.
Vignette
In the Classroom
The following vignette highlights the type of conversations that teachers should have with students when discussing equivalent expressions. Teachers need to help students focus on the underlying structure behind a problem to highlight the algebraic ideas. The teacher wants her students to be able to explain why $(x+1)(x-1)$ is equivalent to $x^{2}-1$. The teacher begins with numbers then selects examples that have a similar structure but with different numbers. She tries to get students to notice how the equation is changing and how it is staying the same. Eventually she wants her students to generate a conjecture. She then directs the class to come up with a justification for the conjecture.
|
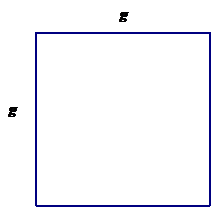
Ms. B: [Writes $(16)(18)=17^{2}-1$ on the board.] Ms. B: Raise your hand if you can tell me if this equation is true or false? Christy: It is true. Ms. B: Why? Christy: Because I put it in my calculator and 16 times 18 is 288. 17 squared is 289 so one less is 288. Both sides are 288. Ms. B: Did anyone else do it a different way? Geoff: I did the same calculations as Christy but I did not use my calculator. Ms. B: OK, what about this equation? Raise your hand if you can tell me if it is true or false. [Writes $(6)(9)=7^{2}-1$ underneath the previous equation.] Ahn: This one is false because six times 9 is 54 and 49 minus one is not 54. Geoff: You should have written six times eight if you wanted it to be true. Ms. B: So is six time eight the same as seven squared minus one? [writes $(6)(8)=7^{2}-1$.] Ahn: Yes, both sides are 48. Ms. B: Let's try to do this without a calculator. What number would $b$ have to be for this equation to be true? [Writes $(245)(247)=b^{2}-1$.] Christy: I am not going to multiply this out. Mick: I think it should be 246, but I am not sure. Ms. B: What made you think that $b$ equals 246? Mick: I noticed that the first two numbers on the left are really close and you are only taking one away from the other side so the square is probably pretty close. Ms. B: Is it exact? Christy: Yes, I checked on my calculator and it works. Geoff: Christy, you weren't supposed to use your calculator. But I think it is right since each true equation has two values that are close. The one [factor] on the left is always less than one of the value being squared and the thing [factor] on the right is always one more than the value. Ms. B: I am not sure what you mean. Geoff: If the value on the right hand side was a $g$ instead of a $b$, [Ms. B writes $(\text{ })(\text{ })=g^{2}-1$.] then inside the parenthesis would be one less and one more. Ms. B: How should I write this? Christy: Write $g$ minus one in the left parenthesis and $g$ plus one in the right. [Ms. B completes the equation as $(g-1)(g+1)=g^{2}-1$.] Yes that is it. Ms. B: So Christy this is your conjecture. Does this rule always work for all values of $g$? Christy: Can we use our calculators? Ms. B: Yes. Please try to find out if this equation is true for any value of $g$. [after 7 minutes] Mick: I think Christy's conjecture works for all numbers. Ms. B: Is that a proof? Mick: No, but I am pretty sure. I know, you have to check every number in the whole world to prove it using numbers, but I checked a lot. Ahn: Maybe we can draw a picture. Ms. B: Good idea. Use your scissors to cut a square that measures $g$ by $g$ from a blank piece of paper.
What is the area of this square? Nancy: $g$-squared. Ms. B: OK, now cut off a small one by one square off the corner of the square.
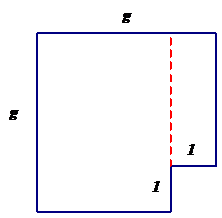
What is the area of this shape? Mick: I think it is $g$-squared minus one. Ms. B: OK. So if the area of this shape is $g^{2}-1$, then if Christy's conjecture is true then the area should also be $(g-1)(g+1)$. See if you can see if this is true. [after 10 minutes]
Ahn: I found that if you cut the square here and move the piece around, you get a new rectangle that is $(g-1)$ by $(g+1)$.
Since the area of the rectangle is the same as the $g^{2}-1$ shape then the conjecture has to always be true. |
Resources
Teacher Notes
- There are many conventions related to mathematical notation that confuse students. This is especially true with grouping symbols. Students seem to understand how to use parentheses correctly when evaluating an expression like $2+3(4-2\cdot 7)$ and learn that they should evaluate the expression inside the parentheses first when evaluating expressions. In fact many people use the mnemonic PEMDAS to remember the order of operations where the P signifies work inside parentheses first. The P should signify all grouping symbols including parentheses. Grouping symbols include absolute value notation (i.e. $2+3|4-2\cdot 7|)$), radical notation (i.e. $\frac{-(-3)\pm\sqrt{(-3)^{2}-4(-2)(7)}}{2(-2)}$), and even brackets (i.e. $3-7[5\cdot 3+4(7-3)]$. These grouping symbols indicate a distinct beginning and end value as parentheses do and students seem to be able to evaluate these expressions with the same success as with parentheses. Students do struggle with implied parentheses and teachers need to be purposeful in discussing and modeling the correct use of these conventions. The expression $\frac{3-8}{2-7}$ has implied grouping symbols in the numerator and the denominator of the fraction. The expression $\frac{3-8}{2-7}$ should be viewed as having implied parentheses in the numerator and the denominator $\frac{(3-8)}{(2-7)}$. Teachers need to model and discuss the use of implied grouping symbols in their classrooms.
- Students need to make sense of adding like and unlike terms. Some students will incorrectly add $2a+3b$ to get $5ab$ or correctly add $2x+3x$ to get $5x$ by memorizing rules. Students need to understand how the distributive property allows them to add and subtract and identify places where they use it. Students who add fractions like $\frac{1}{3}+\frac{1}{2}$ using the common denominator algorithm are actually using the distributive property $\frac{1}{3}+\frac{1}{2}$ can be re-written as $\frac{2}{6}+\frac{3}{6}$ because of equivalent fractions. Students are actually using the distributive property when they add the fractions (i.e. $2\left ( \frac{1}{6}\right ) +3\left ( \frac{1}{6}\right ) =(2+3)\left ( \frac{1}{6}\right )$). Students also use the distributive property when they are adding multi-digit whole numbers like $20+30$ (i.e. $2(10)+3(10)=(2+3)(10)$). This structure is carried through when adding like terms (i.e. $2x+3x=(2+3)x$). Teachers can help students make sense of the distributive property as well as adding like terms using an area model.
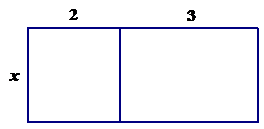
Showing that the area of the rectangle can be calculated in two different ways provides justification as to why the distributive property works with variables.
\begin{matrix}
\underbrace{2x} &+ &\underbrace{3x} &= &\underbrace{(2+3)x)} \\
\textit{area of left} & & \textit{area of right} & & \textit{area of entire} \\
\textit{rectangle} & & \textit{rectangle} & & \textit{rectangle}
\end{matrix}
- The area model is a great way to help students keep track of partial products when multiplying polynomials. Each of the polynomials to be multiplied represents the length and the width of a rectangle. The area of the entire rectangle represents the product of the two polynomials. This area can be found by summing the partial products.
The product $2x\cdot(x^{2}+3x+5)$ can be represented by the following rectangle:
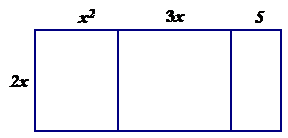
The area of each of the three smaller rectangles represents the partial products.
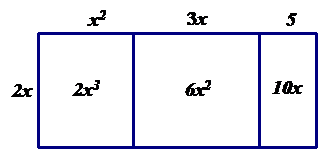
The area of the entire rectangle represents the product which is $2x^{3}+6x^{2}+10x$.
The product of $(x^{2}-3x+9)(x+2)$ can be represented by the following rectangle:
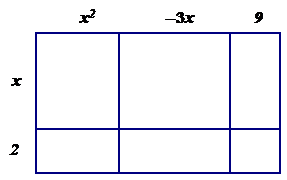
All of these models represent the application of the distributive property.
- Factoring is a process to convert a polynomial expression into a product of polynomials. Factoring is an inverse process of multiplication. An area model is useful for students to negotiate the distributive property when multiplying two polynomials; it is also an accessible model for factoring.
Algebra tiles are an area model and are often used to help students make sense of factoring polynomials. Algebra tiles can be made using card stock or they can be used virtually on a computer. The National Library of Virtual Manipulatives (http://nlvm.usu.edu/) provides access to virtual algebra tiles. The screen capture below represents the polynomial $2x^{2}+7x+3$..
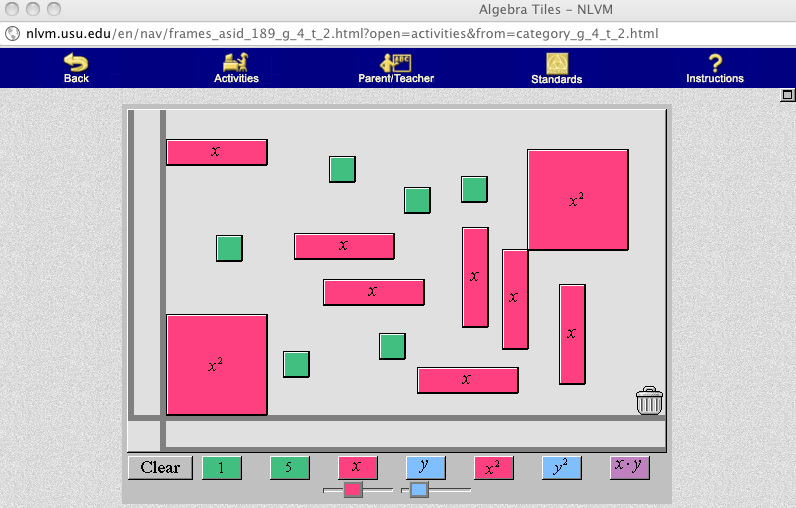
Students need to rearrange all of the rectangles in the figure above to form one large rectangle with no overlaps or gaps.
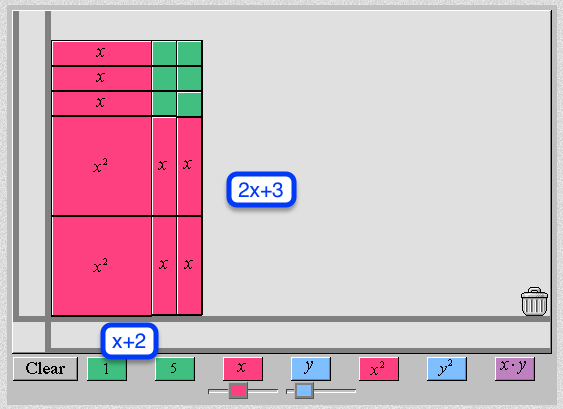
The length of the new large rectangle is $2x+3$ and the width is $x+2$. The area of the large rectangle can be written as the product of the length and width as $(2x+3)(x+2)$. The equation $2x^{2}+7x+6=(2x+3)(x+2)$ is true for all values of $x$ because both expressions count the same area. The virtual manipulative shown does not work with polynomials that have negative coefficients. Algebra tiles made using card stock or commercially available plastic sets can be used to represent polynomials with negative coefficients but the complexity makes it unsuitable as an initial model.
Pictures of rectangles can be used to help students make sense of factoring with polynomials involving large or even negative coefficients. Factoring the expression $m^{2}+4m-21$ can be thought of finding the dimensions of a rectangle with an area of $m^{2}+4m-21$. If students multiply binomials using an area model enough to see the underlying structure then they should be able to reason that a beginning rectangle might look like the one shown below:
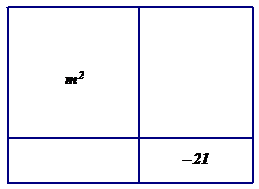
Furthermore they should be able to reason that the sum of the areas of the two unlabeled rectangles need to sum to $4m$. Students can use guess and check to find two numbers that multiply to be $-21$ and sum to $4$. The factored form of the polynomial is the product of the length and width of the rectangle (i.e. $(m+7)(m-3)$). This model is more abstract than the algebra tile model and is a bridge to more symbolic methods.
Instructional Resources:
This interactive pan balance allows numeric or algebraic expressions to be entered and compared. You can "weigh" the expressions you want to compare by entering them on either side of the balance. Using this interactive tool, you can practice arithmetic and algebraic skills, and investigate the important concept of equivalence.
Using tiles to represent variables and constants, learn how to represent and solve algebra problem. Solve equations, substitute in variable expressions, and expand and factor.
Additional Instructional Resources:
Students find the edge length of an octahedron given its volume. First, students find a formula for the edge length of a square given its area. After testing this formula by comparing points on its graph with the measurements of a model square, they write an equivalent formula with fractional exponents and substitute values to find the edge length of a particular square. Students will repeat this process for the formula for the edge length of a cube given its volume. Finally, students solve an equation involving several different radical expressions to find a formula for the edge length of an octahedron given its volume, and use it to solve the original problem.
- nth root: In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals x. $r^{n}=x$
- Factor: The numbers and variables that are multiplied in an expression. Examples: 4 and 9 are factors of 36, 6 and x are factors of 6x
- Factor completely: To write a polynomial as the product of monomial factors or as the product of prime factors with at least two terms. Examples:
$x^{2}+5x+6=(x+2)(x+3)$
$x^{3}-8=(x-2)(x^{2}+2x+4)$
$5x^{3}+10x^{2}-25x=5x(x^{2}+2x-5)$
- Term: A part of an algebraic equation or a number in a sequence or a series or a product of real numbers and/or variables.
- Coefficient: A factor of the term. x is the coefficient in the term x(a + b) or 3 is the coefficient in the term 3y.
- Degree: The degree of an equation is the maximum number of times any variable or variables are multiplied together in any single term. The degree of an equation is used to help decide how to solve an equation, or whether or not an equation has a solution.
- Like terms: Terms that contain the same variables raised to the same exponents.
$3x$ and $2x$ are like terms
$8x$ and $3y$ are not like terms
$3x^{2}$ and $5x^{2}$ are like terms
- Polynomial Expression: An expression with one variable of the form $a_{0}x^{n}+a_{1}x^{n-1}+\cdots a_{n-1}x+a_{n}$ where the coefficients of $a_{0},a_{1},\cdots,a_{n}$ represent complex numbers, $a_{0}$ is nonzero and $n$ represents a nonnegative integer. Example: $p(x)=5x^{5}+4x^{3}+2x^{2}+3x-7$
- Difference of two squares: When a number is squared, or multiplied by itself, and is then subtracted from another squared number. It refers to the identity $a^{2}-b^{2}=(a-b)(a+b)$.
Professional Learning Communities
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- Do my students understand the difference between evaluating expressions and simplifying expressions?
- Are my students able to use the commutative, associative, and distributive properties properly and explain when they are doing so?
- Can my students give reasons why two expressions are equivalent?
Materials - suggest articles and books
- Driscoll, Mark. Fostering Algebraic Thinking.
- Akyuz, D. & Dixon, J. (2009). Quadratic equations and "Cut-and-paste" geometry. On-Math, Volume 7 (1).
References
- Common Core State Standards
- Ellis, M. W., & Bryson, J. L. (2011). Absolute value equations and inequalities: A conceptual approach. Mathematics Teacher, 104 (8), 592-595.
- Ruddell, M.R., & Shearer, B.A. (2002). "Extraordinary," "tremendous," "exhilarating, "magnificent": Middle school at-risk students become avid word learners with the vocabulary self-collection strategy (VSS). Journal of Adolescent & Adult Literacy, 45, 352-363.
Assessment
Assessment
|
Example Item 1
If $f(x)=4x^{2}-7x+5.7$, what is the value of $f(3.5)$? Answer:____________________
Source: NAEP Grade 12, 1992, Question M7-9 Correct Answer: 30.2 Cognitive Level: Hard (39.03% correct)
|
|
Example Item 2
Three students sold pizzas to raise money. Dwayne sold x pizzas. Tamara sold x+20 pizzas. Rueben sold 3(x+20) pizzas. Which of these expressions represents the total number of pizzas that all three students sold? A. $x(x+20)\cdot 3(x+20)$ B. $x+(x+20)+3(x+20)$ C. $\frac{x(x+20)+3(x+20)}{3}$ D. $\frac{x+(x+20)+3(x+20)}{3}$
Source: Maryland High School Assessment Algebra/Data Analysis - Item 36 Correct Answer: B Cognitive Level: Knowledge
|
|
Example Item 3
Which expression shows the complete factorization of $12x^{2}-147$? A. (3x-7)(4x+2) B. (4x-21)(3x+7) C. 12(x-7)(x+7) D. 3(2x-7)(2x+7)
Source: California Standards Test Released Items - Item 19 Correct Answer: D Cognitive Level: Knowledge
|
|
Example Item 4
Suppose that $a_{1},a_{2},a_{3},\cdots$ is the sequence of numbers such that $a_{1}=3,a_{2}=\sqrt{a_{1}}+1,a_{3}=\sqrt{a_{2}}+1$, and, in general, $a_{n+1}=\sqrt{a_{n}}+1$ for all $n\geq 1$. To the nearest hundredth, the value of $a_{5}$ is A. 1.63 B. 2.62 C. 2.73 D. 3.24 E. 5.73
Source: NAEP Grade 12, 1990, Question M9-20 Correct Answer: B Cognitive Level: Hard (25.12% correct)
|
|
Example Item 5
Source: California Standards Test Released Items Correct Answer: B Cognitive Level: Knowledge |
Differentiation
Struggling Learners
- One approach to helping students who struggle with operations involving polynomial expressions is to highlight the same structure that is used when students operate on whole numbers. A student who is having trouble adding $(3x^{2}+2x+7)+(4x^{2}+2)$ should be asked to explain how they add $327+402$. The teacher should question the student enough to highlight the associative, commutative, and the distributive properties they used to carry out the addition and show how expanded notation highlights the steps the student used.
|
$327+402$ |
original problem |
|
$3(10^{2})+2(10)+7(1)+4(10^{2})+0(10)+2(1)$ |
expanded notation |
|
$3(10^{2})+4(10^{2})+2(10)+0(10)+7(1)+2(1)$ |
commutative property of addition |
|
$(3+4)(10^{2})+(2+0)(10)+(7+2)(1)$ |
distributive property of multiplication over addition |
Although students may use different vocabulary than is described here the underlying structure is the same. This same sort of strategy can be used with multiplication and subtraction of polynomials.
English Language Learners
- It is very important for students to be able to match the directions of a problem with the problem types that would match these directions.
Students would get a copy of the following sheet and they would cut out each problem card.
|
A $x^{2}+5x-10$ |
B $x^{2}-9=0$ |
C $(x+3)(x-7)$ |
|
D $3+7|2-7x|$ |
E $(x^{3}-3x^{2}+7)\div (x+1)$ |
F $\sqrt{2x+5}+7$ |
|
G $\frac{x^{2}-4x-21}{x-7}$ |
H $6x^{2}-3x-63$ |
I $\frac{20}{x-7}$ |
The teacher would write the word "Factor" on the board and ask the students to sort the cards into two piles, one pile for problems that would make sense to factor and another pile for problems that would not make sense to factor. The direction of "Factor" matches the problems on cards A and H. The equation on card B would not match even though a student might solve the problem by factoring. The matching directions for the problem on card B would be to "Solve" or "Solve by Factoring". After the students agree to which cards match, the students would then be asked to follow the directions for each problem that matches. Other directions that could be asked by the teacher include: "Divide", "Multiply", "Evaluate when $x=2$", and "Solve".
Extending the Learning
- Students need to apply their knowledge of absolute value in a different way to answer this question.
|
Find the exact value of $|\pi-3.14|+\left | \pi-\frac{22}{7}\right | $
|
Students need to decide if the absolute value grouping symbols are essential or non-essential. The exact value of $\pi$ is larger than $3.14$ so $|\pi-3.14|=\pi-3.14$. The exact value of $\pi$ is less than $\frac{22}{7}$ so $|\pi-\frac{22}{7}|=\frac{22}{7}-\pi$.
$|\pi-3.14|+|\pi-\frac{22}{7}|$
$\pi-3.14+\frac{22}{7}-\pi$
$\frac{22}{7}-3.14$
$\frac{22}{7}-\frac{314}{100}$
$\frac{2200}{700}-\frac{2198}{700}$
$\frac{2}{700}$
$\frac{1}{350}$
Parents/Admin
|
Students are: (make list) |
Teachers are: (make list) |
|
|
|
|
|
|
Parent Resources: suggested activities, materials, websites
This website shows a visual area modeling with Algebra Tiles to demonstrate adding/subtracting, multiplying, and dividing polynomials, factoring, and completing the square.