9.4.1 Describe & Analyze Data
Describe a data set using data displays, including box-and-whisker plots; describe and compare data sets using summary statistics, including measures of center, location and spread. Measures of center and location include mean, median, quartile and percentile. Measures of spread include standard deviation, range and inter-quartile range. Know how to use calculators, spreadsheets or other technology to display data and calculate summary statistics.
Analyze the effects on summary statistics of changes in data sets.
For example: Understand how inserting or deleting a data point may affect the mean and standard deviation.
Another example: Understand how the median and interquartile range are affected when the entire data set is transformed by adding a constant to each data value or multiplying each data value by a constant.
Use scatterplots to analyze patterns and describe relationships between two variables. Using technology, determine regression lines (line of best fit) and correlation coefficients; use regression lines to make predictions and correlation coefficients to assess the reliability of those predictions.
Use the mean and standard deviation of a data set to fit it to a normal distribution (bell-shaped curve) and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets and tables to estimate areas under the normal curve.
For example: After performing several measurements of some attribute of an irregular physical object, it is appropriate to fit the data to a normal distribution and draw conclusions about measurement error.
Another example: When data involving two very different populations is combined, the resulting histogram may show two distinct peaks, and fitting the data to a normal distribution is not appropriate.
Overview
Students have had experiences with collecting, organizing, displaying, interpreting, drawing conclusions, and making predictions with data. The focus of instruction at the high school graduation standard level is on expanding and building more sophisticated ways to analyze data graphically, verbally, and symbolically to describe relationships and draw conclusions from data in light of variability. Students "can use their expanding repertoire of algebraic functions, especially linear functions, to model and analyze data, with increasing understanding of what it means for a model to fit data well" (NCTM, 2000). The activities should focus on the use of technology to allow students to focus on conjectures and statistical reasoning. Technology in the form of spreadsheets, calculators, dynamic software, and web applets can assist students in displaying and interpreting data. "Education in a free society must prepare citizens to make informed choices in all areas of their lives. They must be able to grasp the information being presented, analyze it, and make reasoned decisions" (Massachusetts Framework, 2000, p.12).
All Standard Benchmarks
9.4.1.1 Describe a data set using data displays, including box-and-whisker plots; describe and compare data sets using summary statistics, including measures of center, location and spread. Measures of center and location include mean, median, quartile and percentile. Measures of spread include standard deviation, range and inter-quartile range. Know how to use calculators, spreadsheets or other technology to display data and calculate summary statistics.
9.4.1.2 Analyze the effects on summary statistics of changes in data sets.
For example: Understand how inserting or deleting a data point may affect the mean and standard deviation.
Another example: Understand how the median and interquartile range are affected when the entire data set is transformed by adding a constant to each data value or multiplying each data value by a constant.
9.4.1.3 Use scatterplots to analyze patterns and describe relationships between two variables. Using technology, determine regression lines (line of best fit) and correlation coefficients; use regression lines to make predictions and correlation coefficients to assess the reliability of those predictions.
9.4.1.4 Use the mean and standard deviation of a data set to fit it to a normal distribution (bell-shaped curve) and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets and tables to estimate areas under the normal curve.
For example: After performing several measurements of some attribute of an irregular physical object, it is appropriate to fit the data to a normal distribution and draw conclusions about measurement error.
Another example: When data involving two very different populations is combined, the resulting histogram may show two distinct peaks, and fitting the data to a normal distribution is not appropriate.
Benchmark 9.4.1.1 Describe a data set using data displays, including box-and- whisker plots; describe and compare data sets using summary statistics, including measures of center, location and spread. Measures of center and location include mean, median, quartile and percentile. Measures of spread include standard deviation, range and inter-quartile range. Know how to use calculators, spreadsheets or other technology to display data and calculate summary statistics.
Benchmark 9.4.1.2 Analyze the effects on summary statistics of changes in data sets.
Benchmark 9.4.1.3 Use scatterplots to analyze patterns and describe relationships between two variables. Using technology, determine regression lines (line of best fit) and correlation coefficients; use regression lines to make predictions and correlation coefficients to assess the reliability of those predictions.
Benchmark 9.4.1.4 Use the mean and standard deviation of a data set to fit it to a normal distribution (bell-shaped curve) and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets and tables to estimate areas under the normal curve.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Students will be able to make decisions about how to display and analyze real world data based on statistical thinking. Students will know that data does not always send a clear message and is often obscured by variability.
- Students will be able to look at two variables to determine the strength of the relationship and the reliability of predictions that can be made.
- Students will know that "data are gathered, displayed, summarized, examined, and interpreted to discover patterns and deviations from patterns." "Which statistics to compare, which plots to use, and what the results of a comparison might mean, depend on the question to be investigated and the real-life actions to be taken" (Common Core Standards, 2010, p. 80).
- Students will be able to use technology to display and analyze data and calculate summary statistics.
- Students will be able to use statistical models to describe possible associations between measurement variables and will be adept with techniques for fitting models to data.
- Students will be able to differentiate between correlation and causation.
- Students will understand sample variability in data that comes from larger populations.
- Students will understand the influence that certain data points have on statistics.
- Students will have exposure to how companies use statistics to make decisions. The idea of "data-mining" by Internet sites to better serve customers should also be explored.
- Students will be able to see that many fields of study use probability and statistics.
Work from previous grades that supports this new learning
● Students entering high school can pose questions, collect data, and select appropriate display(s) from among scatterplots, bar graphs, tables, and circle graphs. (Minnesota Mathematics Framework-Data Investigation, 1997).
- Students have explored lines of best fit.
- Students can calculate and interpret mean, median, and range. They have begun to develop an intuitive sense for spread and deviation.
- Students can make an educated guess to estimate the effect of changes in key portions of the data on measures of center.
- Students can read, write, represent, and compare rational numbers expressed as fractions, decimals, percents, and ratios.
- Students have used a variety of technologies to create visual representations of data.
- Students have used a variety of graphical summaries to compare data sets.
NCTM Standards
Data Analysis and Probability Standards
In grades 9-12 all students should:
- formulate questions that can be addressed with data and collect, organize and display relevant data to answer them
- understand the meaning of measurement data and categorical data, of univariate and bivariate data, and of the term variable;
- understand histograms, parallel box plots, and scatterplots and use them to display data
- compute basic statistics and understand the distinction between a statistic and a parameter.
- select and use appropriate statistical methods to analyze data
- for univariate measurement data, be able to display the distribution, describe its shape, and select and calculate summary statistics
- for bivariate measurement data, be able to display a scatterplot, describe its shape, and determine regression coefficients, regression equations, and correlation coefficients using technological tools
- display and discuss bivariate data where at least one variable is categorical
- recognize how linear transformations of univariate data affect shape, center, and spread
- identify trends in bivariate data and find functions that model the data or transform the data so that they can be modeled.
Common Core State Standards (CCSS)
Statistics and Probability Standards
Interpreting Categorical and Quantitative data S-ID
Summarize, represent, and interpret data on a single count or measurement variable
- Represent data with plots on the real number line (dot plots, histograms, and box plots).
- Use statistics appropriate to the shape of the data distribution to compare center (median, mean) and spread (interquartile range, standard deviation) of two or more different data sets.
- Interpret differences in shape, center, and spread in the context of the data sets, accounting for possible effects of extreme data points (outliers).
- Use the mean and standard deviation of a data set to fit it to a normal distribution and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets, and tables to estimate areas under the normal curve.
Summarize, represent, and interpret data on two categorical and quantitative variables
- Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
- Fit a function to the data; use functions fitted to data to solve problems in the context of the data. Use given functions or choose a function suggested by the context. Emphasize linear and exponential models.
- Informally assess the fit of a function by plotting and analyzing residuals.
- Fit a linear function for a scatter plot that suggests a linear association.
Interpret linear models
- Interpret the slope (rate of change) and the intercept (constant term) of a linear model in the context of the data.
- Compute (using technology) and interpret the correlation coefficient of a linear fit.
Misconceptions
Student Misconceptions and Common Errors
- Losing track of the real world context of the data and only focusing on procedures.
- Students have difficulties properly scaling the axes. Students often scale their axes so that every relationship looks linear.
- Time plots can lead students to make an axis that represents the actual years. In some cases, it is more appropriate to label the axis in terms of "years since" some starting date.
- When a student uses technology (graphing calculators) to make plots they often miss the thinking (deeper understanding of the problem) that comes from determining the proper scaling to show relationships. There is often an issue with what is a "line"? As in all mathematics, a line means a "straight" line. Students need to be able to distinguish linear relationships from other types (exponential, power, quadratic, etc.) and if they use the term "line" to describe a curved pattern they will have issues with linear relationships versus non-linear relationships.
- Students think that the middle of a box and whisker plot is the mean. Often students do not relate the five number summary (minimum, first quartile, median, third quartile, and maximum) to the marks in a box and whisker plot. When a student makes a plot without scale they will make the quartiles the same length. This does not allow the student to see the shape of the distribution (skewed, normal, etc.)
- Students think of variability only in terms of the range of data.
- Many words have very technical meanings in statistics such as bias, sample, statistics, accuracy, correlation, random, normal, confident, and significant. Students can have difficulty with the language. "Rather studying statistics is akin to studying foreign language, for students need lots of practice to become comfortable using these terms correctly" (Rossman, Chance, & Medina, 2006, p. 10).
- The idea that statistics come from a sample taken from a larger population and is only representative of the population is a common issue. Often the term "statistic" is used to describe the summary analysis from an entire population. When comparing the summary data from two populations comparisons are definite and the difference can be stated as such. When the data is a statistic from a sample taken from a larger population the comparison introduce some uncertainty. People often want to have definitive comparisons from data sets and this is simply not statistically possible when dealing with samples.
Vignette
In the Classroom
The goal for this lesson is to have students describe data for the winning 100 meter dash times of men and women from the Olympics graphically and verbally. Based on their analysis of data, students will have to make statements or claims that they can support with their graphical displays or summary statistics. Students will then use regression lines to make predictions for the winning times in future Olympics. This lesson can incorporate technology in the form of graphing calculators, spreadsheets, the free statistical program R or the program Fathom, depending on the preference of the teacher. (Note: Fathom comes with the data in a sample document with times through 2004). Students have had previous experiences with calculating and interpreting summary statistics. They have explored box plots and lines of best fit.
The teacher begins the lesson by having students read through the article below and discuss the questions that follow. After a short class discussion, the teacher provides students with the data on the 100 meter dash winning times in the Olympics for men and women. Students work in groups of three to graphically and verbally describe the data. Students are to come up with three statements that they can support graphically or with summary statistics.
Jamaican Sprinters: Small Country, Large Olympic Success
Jamaica has the prestigious honor of having the most success per capita of any country in the world in track and field. This great honor started when Jamaica's first track Gold Medalist Dr. Authur Wint won the 400m in 1948 Olympics. Track and field is ingrained in Jamaica as the majority of the schools in Jamaica have a track program in their curriculum. The annual National Boys and Girls Championship which is held at the National Stadium in Kingston is the premier event for track and field in Jamaica where future track athletes showcase their skills to the rest of the island and also to the many overseas recruits who attend this event. Jamaica's track and field athletes are acknowledged to be among the best in the world and many of them have gone on to represent other countries, including Donovan Bailey, Linford Christie, Juliet Campbell, Merlene Frazier, Ben Johnson, and Maria Jose. 2008 Bejing Olympics Jamaican sprinters
Melaine Walker: Gold 400 meter hurdles
Veroncia Campbell-Brown: Gold 200 meter dash
Kerron Stewart: Silver 100 meter dash
Sherone Simpson: Silver 100 meter dash
Asafa Powell, Michael Frater & Nesta Carter: Gold 4x100 meter relay
|
|
|
|
Usain Bolt: Gold 100 meter dash, 200 meter dash, 4x100 meter relay |
Shelly-Ann Fraser: Gold 100 meter dash |
Questions
1. Why do you think the Jamaican sprinters have had so much success in Track and Field?
2. Do you think that the winning times in the 100 meter dash in the Olympics have gotten slower or faster throughout the years? Give an explanation for your answer.
3. Is there a limit to how fast humans will be able to run?
4. How has technology enabled more accurate measurements to be taken?
Teacher: Let's have a couple groups share their statements and how they will support the statements with the data.
Student: We used the summary statistics for our first statement. On average men are faster than women. This is supported by the mean of the men's 100 meter dash being a smaller number than the mean of the women's 100 meter dash.
Teacher: Does anyone see any evidence for disagreeing with this statement?
Student: Men have been competing in the Olympics longer so over time women might be able to catch up with the men.
Teacher: How could you investigate if women are catching up to the men?
Student: We could take the differences in each year and see if they are getting smaller
Summary Statistics
|
|
Men's 100 meter dash |
Women's 100 meter dash |
|
Mean |
10.358 |
11.231 |
|
n |
26 |
19 |
|
Standard Deviation |
0.512 |
0.453 |
|
Standard Error |
0.1 |
0.104 |
|
Minimum |
9.69 |
10.54 |
|
Q1 |
9.96 |
10.93 |
|
Median |
10.275 |
11.07 |
|
Q3 |
10.8 |
11.5 |
|
Maximum |
12 |
12.2 |
|
Range |
2.31 |
1.66 |
(Students figure out the differences from the data table)
|
Year |
Women's Winning Time |
Men's Winning Time |
Difference in times |
|
1896 |
|
12 |
|
|
1900 |
|
10.8 |
|
|
1904 |
|
11 |
|
|
1908 |
|
10.8 |
|
|
1912 |
|
10.8 |
|
|
1920 |
|
10.8 |
|
|
1924 |
|
10.6 |
|
|
1928 |
12.2 |
10.8 |
1.4 |
|
1932 |
11.9 |
10.3 |
1.6 |
|
1936 |
11.5 |
10.3 |
1.2 |
|
1948 |
11.9 |
10.3 |
1.6 |
|
1952 |
11.5 |
10.4 |
1.1 |
|
1956 |
11.5 |
10.5 |
1 |
|
1960 |
11 |
10.2 |
0.8 |
|
1964 |
11.4 |
10 |
1.4 |
|
1968 |
11 |
9.9 |
1.1 |
|
1972 |
11.07 |
10.14 |
0.93 |
|
1976 |
11.08 |
10.06 |
1.02 |
|
1980 |
11.6 |
10.25 |
1.35 |
|
1984 |
10.97 |
9.99 |
0.98 |
|
1988 |
10.54 |
9.92 |
0.62 |
|
1992 |
10.82 |
9.96 |
0.86 |
|
1996 |
10.94 |
9.84 |
1.1 |
|
2000 |
10.75 |
9.87 |
0.88 |
|
2004 |
10.93 |
9.85 |
1.08 |
|
2008 |
10.78 |
9.69 |
1.08 |
Student: Between 1980 and 1988 women closed the gap by about 0.8 seconds, but since that time the gap has been about 1 second.
Teacher: So it looks like while times for men and women have been decreasing since 1952 the time difference has been relatively close to one second. Both men and women are getting faster. Let's have another group share one of their statements.
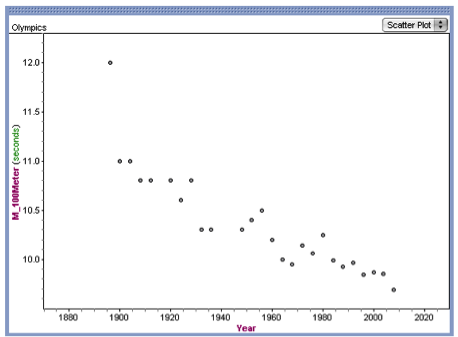
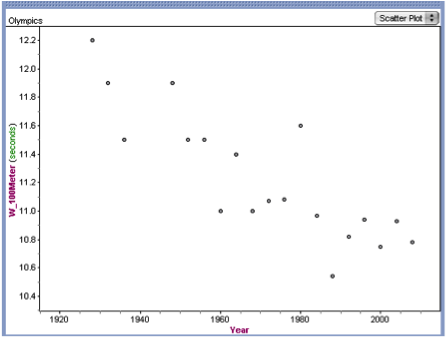
Student: For this statement we used the scatter plots. We felt that both the men's and women's scatterplot appeared to have a fairly linear relationship.
Scatter Plots
|
|
|
Teacher: How could we check if a linear model was a good fit for the data?
Student: We could do a line of best fit.
Teacher: How could we tell from the line of best fit if a linear model is good?
Student: If the points are close to the line, then the linear model is a good fit. If they are farther away then it would not fit the data well.
Teacher: Good, there is a way to figure out what you mentioned that is called a correlation. A correlation describes the relationship between two data sets. If the data is perfectly linear then the correlation is 1 or -1; if the data is not a good linear fit at all it will be closer to 0. How do you think you could tell if the correlation will be positive or negative?
Student: I think it might have to do with slope since correlation is a relationship between data. If the correlation is negative the line slopes down and if it is positive the line will slope up.
Teacher: Make a prediction in your group for what you think the correlation coefficients will be. Then go ahead and calculate the line of best fit and see what the equation is and the correlation coefficient.
(Students work in groups using Fathom or graphing calculators to calculate the equations.)
|
|
Men's |
Women's |
|
Line of best fit |
(100 meter time) = -0.01306 (Year) + 11.119 |
(100 meter time) = -0.01576 (Year) + 12.41 |
|
Correlation coefficient |
-0.895 |
-0.847 |
|
r-squared |
0.801 |
0.718 |
Note: Values for Year were converted to years since 1896.
Teacher: How can you see in the graph that the correlation for the men's times will be higher than the correlation for the women's times?
Student: The men's times appeared to be more consistent since they are bunched closer together. There is just one point that does not fit the pattern well.
Teacher: What would we call that point on the men's scatter plot?
Student: A slow man.
Teacher: Compared to the other times, that point represents a slower time so that is right. If a value is far from the other values in a data set we can call it an outlier as well. What do you think would happen to the men's median, mean, and standard deviation if we were to exclude that point?
(Students talk in groups about what would happen to the mean, median, and standard deviation.)
Teacher: Let's have you share your ideas.
Student: I think that the standard deviation is going to get bigger because all the points would be pretty close together then. The median would not change much because we are just getting rid of one point. The mean should get smaller, because there is a maximum value that we are getting rid of.
Student: I think that the standard deviation will get smaller because that point is farther away from the other points.
Teacher: It might help if someone explains what the standard deviation is.
Student: It is how far on average the individual parts are away from the mean.
Teacher: That is on the right track, we can be more precise though if we say that it is a measure of how much variation there is from the mean.
Teacher: Is the point that we are excluding closer to or farther away from the mean compared to the other points?
Student: Farther away, so the standard deviation should get smaller.
Teacher: Let's go ahead and see what happens
|
|
Men's 100 meter dash |
Men's 100 meter dash 1986 value removed |
|
Mean |
10.358 |
10.293 |
|
Median |
10.275 |
10.25 |
|
Standard Deviation |
0.512 |
0.396 |
(Class discusses what would happen in other situations if multiple different points were added or deleted.)
Teacher: Let's hear from another group that used the box plots to make a statement
Student: Our group feels that at least 50% of the men's winning times were faster than the fastest women's winning time.
Box plots
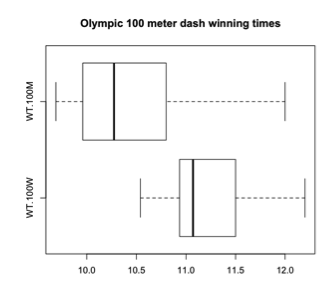
Teacher: Where do you see the 50% of the men's fastest times?
Student: For the men's box plot since the line in the middle of the box is the median, than everything to the left of the median is half of the data. The fastest time for the women is to the right of the men's median.
Teacher: Is there a large difference in the winning times?
Student: There are a lot of times grouped together for the men, but the fastest women's time is only about 0.8 seconds away from the fastest men's time. So, while 50% of the men's times are faster than the fastest women's time, they are still relatively close.
(Teacher wraps up the lesson by having students talk in their groups and write up answers to the following questions that they will hand in before they leave.)
Questions
1. How can you tell if there appears to be a relationship between data?
2. How can you tell if there is a linear relationship?
3. Explain how adding or deleting values can affect the mean, median, and standard deviation.
How can you tell how strong or weak a relationship is between data?
Sources:
Resources
Teacher Notes
- Students may need support in further development of a broad view of variability. They should have opportunities to explore variability and make comparisons of variability within the context of data presented in different kinds of graphs. "Instructors should explicitly discuss the concept of variability of data in general and not limit the focus to quantifying variability through common measures such as range, interquartile range, and standard deviation" (Cooper & Shore, 2008, p. 11). Variability can be naturally occurring due to the diversity of people, places, or events or can involve measurement error.
- Students may need support in properly scaling graphs when using technology. Teachers can relate how students scale graphs when making them by hand to scaling graphs with technology.
- Students may need support in further development of vocabulary. Teachers can give students opportunities to explore and demonstrate their understanding of concepts in multiple ways.
- Students may need support in comparing the statistical differences in data sets and the practical differences in the data.
- Students need exposure to misuses of statistics. Students need to understand that different people looking at the same data can come to completely opposite conclusions. Students should be cautious of conclusions without seeing the raw data.
Students model linear data in a variety of settings that range from car repair costs to sports to medicine. Students work to construct scatterplots, interpret data points and trends, and investigate the notion of line of best fit.
This Unit Plan consists of lessons in which students interpret the slope and y-intercept of least squares regression lines in the context of real-life data. Students use an e-example applet to plot the data and calculate the correlation coefficient and equation of the least squares regression line. These lessons develop skills in connecting, communicating, reasoning, and problem solving as well as representing fundamental ideas about data.
In this activity, students will use the Illuminations Line of Best Fit Activity to plot the data from two teams during the 2004‑05 NBA season. In particular, students will look at the data for total points and minutes played by each of the starters on the Los Angeles Lakers and Detroit Pistons. The data suggest that Laker Kobe Bryant is an outlier-he scores more points per minutes than his teammates, which is part of why some sportswriters have described him as "selfish." But through further investigation, students will also notice that Piston Ben Wallace is also an outlier, because he scores fewer points than his teammates.
Additional Instructional Resources
- Fathom (Fathom Dynamic Statistics Software). B. Finzer, Key Curriculum Press, 150 65th Street, Emeryville, CA 94608.
Fathom's features include dynamic manipulation, that is, instantaneous updating of every representation and calculation while dragging data points, axes, attributes, or bars; formulas to calculate values, plot functions, and control simulations; "sliders" as part of function plotting, attribute definition, and filters; simple simulation and sampling tools; and direct import of data from the Internet.
(Note: Fathom software is not free.)
Collections of Data Sets
- While Fathom Dynamic Data comes equipped with more than 300 diverse data sets, the software is also compatible with a wide range of independent data. The links at this website have a variety of collections of data-ranging from lunar eclipses to a baseball player's batting average-that can be easily integrated into the Fathom software for further exploration of real-world statistics.
- GuessingCorrelations. The CUWU Statistics Program, DepartmentofStatistics, University of Illinois at Urbana-Champaign, Urbana, IL 61820. A Java applet to show the relationship between correlations and scatterplots.
- The Data and Story Library (DASL). DASL Project, Cornell University, 358 Ives Hall, Ithaca, NY 14850-3901. This is an online library of data files and stories that illustrate the use of basic statistical methods.
- Journal of Statistics Education. An international journal on the teaching and learning of statistics.
- The Exploring Data-Math Forum This site provides standards, datasets, lessons and websites at the K-4, 5-8, and 9-12 levels.
- Texas Instruments Classroom Activities Exchange Activities can be used to supplement lessons on the concepts in Gr. 9-12 Data Analysis and Probability.
Websites for real world data
"Different statisticians may come up with somewhat different analyses of a given set of data, but will usually agree on the main conclusions and only worry about minor points if those points matter to the client" (American Statistical Association (ASA), 2007, p. 15).
Suggestions for teachers include the following: Modeling statistical thinking for students, use technology, have students practice statistical thinking, plenty of practice with choosing appropriate questions and techniques, and give feedback on statistical thinking. There are many types of real data including archival, classroom-generated and simulated data. "Few data sets interest all students, so one should use data from a variety of contexts" (ASA, 2007, p. 16).
- The Machine Learning Repository includes data sets both large and small, and those listed under CS/Engineering cover some topics on themes raised in this paper, such as fraud detection in hacker attacks on computers.
- Theinfo.org
- Data and story library
- Australian data and story library
- An NSF project on projects for introductory statistics classes
- City Data Site
- State and county statistics sites
- State and national Dept.'s of Education
- County tax assessment records
- Applebee's
- Arby's
- Burger King
- McDonalds
- Ruby Tuesday's
- Sports Statistics Data Resources (Gateway)
- NFL Historical Stats
- Cost/Prices, e.g., Kelley Blue Book:
- Consumer Report ratings
correlation: a measure of the relationship between two data sets (positive, negative or no correlation). (Anoka)
interquartile range (IQR): the difference between the first quartile point and the third quartile point. (Anoka)
line plot: a method of visually displaying a distribution of data values where
each data value is shown as a dot or mark above a number line. Also known as a
dot plot. (CC)
mean absolute deviation: a measure of variation in a set of numerical data,
computed by adding the distances between each data value and the mean, then
dividing by the number of data values. Example: For the data set {2, 3, 6, 7, 10,
12, 14, 15, 22, 120}, the mean absolute deviation is 20. (CC)
measurement error: the difference between an approximate measurement and the actual measurement taken. (Anoka)
percentile: the data value that a certain percent of the data falls at or below. (Anoka)
sample: a subset of a population.
standard deviation: a measure of the variation in a set of numerical data. It is computed by adding the squared distances between each data value and the mean, dividing by the number of data values, and then taking the square root of the result. Example: For the data set {2, 3, 6, 7, 10, 12, 14, 15, 22, 120}, the standard deviation is approximately 33.46.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- Can students understand how changes in measures of center and spread affect different representations of data?
- How can I facilitate students to explore relevant real world data and support claims based on different graphs and statistics?
- How can I improve on student's procedural and conceptual understanding of measures of center and spread, regression lines, predictions, and decision making?
- What type of data do my students use in their day-to-day lives? How can I incorporate this data into my lessons? Students need to "see" that that use probability and statistics in their lives without the formality they see in class.
Materials - suggested articles and books
American Statistical Association. (2007). Guidelines for assessment and instruction in statistics education. Retrieved December 14th, 2010.
This is the K-12 portion of the American Statistical Association (ASA) website. They have workshops for teachers, online resources for teachers, useful websites, student competitions, and a list of publications in statistics education.
Ben-Zvi, D. (2009). Toward understanding the role of technological tools in statistical learning. Mathematical Thinking and Learning, 2(1), 127-155.
Haberman, M. (1991). The pedagogy of poverty versus good teaching. Phi Delta Kapan, (December). 291-294.
Peck, R., Starnes, D., Kranendank, H., & Morita, J. (2009). Making sense of statistical studies: Teacher's module. Alexandria, VA: American Statistical Association.
This book consists of 15 hands-on investigations that provide students with valuable experience in designing and analyzing statistical studies. It is written for an upper middle-school or high-school audience. Each investigation includes a descriptive overview, prior knowledge that students need, learning objectives, teaching tips, references, possible extensions, and suggested answers.
One of the goals of the American Statistical Association is to improve statistics education at all levels. Through the Statistics Education Web (STEW), the ASA plans to reach out to K-12 mathematics and science teachers who teach statistics concepts in their classrooms. STEW will be an online resource for peer-reviewed lesson plans and resources for K-12 teachers. The web site will be maintained by the ASA and accessible to K-12 teachers throughout the world.
American Statistical Association. (2007), Guidelines for assessment and instruction in statistics education. http://www.amstat.org/education/gaise/index.cfm.
Ben-Zvi, D. (2009). Toward understanding the role of technological tools in statistical learning. Mathematical Thinking and Learning, 2(1), 127-155.
Cooper, L. & Shore, F. (2008). Student misconceptions in interpreting center and variability of data represented via histograms and stem-and-leaf plots. Journal of Statistics Education, 16(2), 1-13.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
Rossman, A., Chance, B., & Medina, E. (2006). Thinking and reasoning with data and chance. Reston, VA: National Council of Teachers of Mathematics. Important comparisons between statistics and mathematics, and why teachers should care.
Assessment
DOK Level 1: Recall
1. A teacher claims that quiz scores for students are indicative of their test scores. Sample 6 students from this teacher's class and find the following quiz and test scores:
|
Quiz scores |
7 |
2 |
9 |
6 |
9 |
5 |
|
Test scores |
85 |
60 |
80 |
70 |
85 |
80 |
2. Draw a scatter plot for these data, with the quiz scores on the horizontal axis and test scores on the vertical axis. Find the line that best fits these data by using least squares and graph the line along with your scatter plot. (California Mathematics Framework, Appendix D, 2005, p. 331).
DOK Level 3: Strategic Thinking
3. In the preceding example concerning quiz scores and test scores, by using the graph alone, what can you say about the correlation coefficient? Suppose that 4 more data points are collected and that the best fit line remains approximately the same for the combined data, but that the correlation coefficient now is closer to 1 than it was for just the 6 data points. What can you say about the placement of the 4 additional data points? (California Mathematics Framework, Appendix D, 2005, p. 331).
DOK level 2: Basic Reasoning
4. Suppose that it is known that the average lifetime of a particular brand of light bulb is 1,000 hours, with a standard deviation of 90 hours. You sampled 20 of these bulbs and computed that their lifetimes averaged 900 hours, with a sample standard deviation of 120 hours. If you sample another 20 bulbs and combine your data, what is most likely to occur to the average lifetimes for the 40 bulbs and to the sample standard deviation for the 40 bulbs? (California Mathematics Framework, Appendix D, 2005, p. 332).
DOK level 2: Basic Reasoning
5. A clock manufacturer has found that the amount of time their clocks gain or lose per week is normally distributed with a mean of 0 minutes and a standard deviation of 0.5 minute, as shown below. In a random sample of 1,500 of their clocks, which of the following is closest to the expected number of clocks that would gain or lose more than 1 minute per week?
A. 15 B. 30 C. 50 D. 70 E. 90
Correct answer: D
Rationale: Students must recall information about the normal curve (that the region between the mean ± 2 standard deviations contains 95 percent of the data), and apply that information to solve the problem. (Mathematics Framework for the 2009 NAEP, 2008, p.46).
DOK level 3: Strategic Thinking
6. Three families are traveling west on the Overland Trail. They are taking the same path the pioneer families did in the 1850s. The families started together 360 miles from their final destination. The graph below shows the line of best fit for the distance each family has left to travel at the end of the first 11 days.
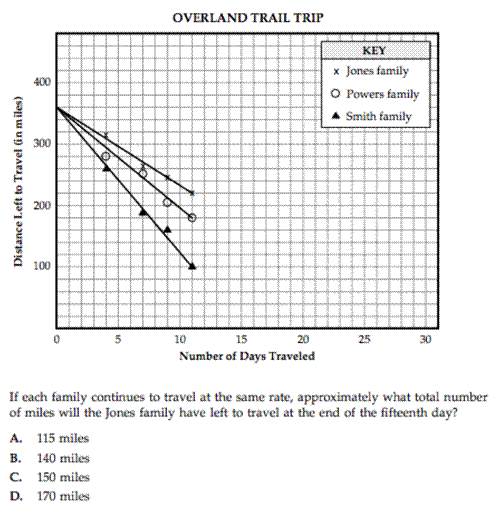
(FCAT 2006 Mathematics released test, Florida Department of Education, http://fcat.fldoe.org/pdf/releasepdf/06/FL06_Rel_G10M_TB_Cwf001.pdf p. 26).
DOK level 2: Basic Reasoning
7. Stephanie scored 88, 70, 84, and 72 on her first four science tests. What score does Stephanie need on her fifth science test to receive a mean score of 80?
A 79 B 80 C 82 D 86
MD Department of Education, 2009, Algebra/data analysis public release, p.4, http://mdk12.org/assessments/high_school/look_like/2009/algebra/hsaAlgebra.pdf
DOK level 3: strategic thinking
8. Nineteen families live in a small town. The income for each family is listed in the table below.

MD Department of Education, 2008, Algebra/data analysis public release, p.19, http://mdk12.org/assessments/high_school/look_like/2008/algebra/hsaAlgebra.pdf
DOK level 3 Strategic thinking
9. The table below shows the population of a small town from 1960 to 1990.

MD Department of Education, 2008, Algebra/data analysis public release, p.26, http://mdk12.org/assessments/high_school/look_like/2008/algebra/hsaAlgebra.pdff
Minnesota Comprehensive Assessment (MCA) III Test Specifications
Standard 9.4.1
Display and analyze data; use various measures associated with data to draw conclusions, identify trends and describe relationships.
Benchmarks
9.4.1.1 Describe a data set using data displays, including box-and-whisker plots; describe and compare data sets using summary statistics, including measures of center, location and spread. Measures of center and location include mean, median, quartile and percentile. Measures of spread include standard deviation, range and inter-quartile range. Know how to use calculators, spreadsheets or other technology to display data and calculate summary statistics.
Item Specifications: Vocabulary allowed in items: box-and-whisker plot, quartile, percentile, inter-quartile range, standard deviation, central tendency and vocabulary given at previous grades
9.4.1.2 Analyze the effects on summary statistics of changes in data sets.
Item Specifications: Vocabulary allowed in items: quartile, percentile, inter-quartile range, standard deviation, central tendency and vocabulary given at previous grades
9.4.1.3 Use scatterplots to analyze patterns and describe relationships between two variables. Using technology, determine regression lines (line of best fit) and correlation coefficients; use regression lines to make predictions and correlation coefficients to assess the reliability of those predictions.
Item Specifications: Vocabulary allowed in items: regression line, correlation coefficient and vocabulary given at previous grades
9.4.1.4 Use the mean and standard deviation of a data set to fit it to a normal distribution (bell-shaped curve) and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets and tables to estimate areas under the normal curve.
Item Specifications: Vocabulary allowed in items: standard deviation, normal distribution, normal curve and vocabulary given at previous grades
(Note: These Test Specifications are in DRAFT form as of May 4, 2011 (updated Test Specifications will be available: http://education.state.mn.us/MDE/Accountability_Programs/Assessment_and_Testing/Assessments/MCA/TestSpecs/index.html)
Differentiation
- Strategies: Real world problem solving, multiple entry points, varied teaching methods, group work, teach problem solving strategies. Teachers can provide skeleton handouts for students or make copies of notes from another student so that special education students can focus on the concepts.
- Challenges: Motivation, slower processing, reading and writing ability, organization, and behavior issues and coping strategies.
Teachers must be explicit in how they talk about vocabulary terms and use vocabulary in context. Teachers should use vocabulary terms often so that students will become familiar hearing them in context. Students should also be allowed to practice the use of vocabulary in small groups.
- Strategies: Model vocabulary, manipulatives, speak slowly, visuals, variety of assessments, group work, verbalize reasoning, understanding context or concept, making personal dictionaries.
- Challenges: Vocabulary and Reading ability, standardized tests, how to approach problem solving, cultural differences.
Minnesota Council for the Gifted and Talented
- Strategies: Tiered objectives, open-ended problem solving, grouping (heterogeneous and homogeneous), curriculum compacting, and independent investigations. Students can be given more challenging work by using activities developed by the University of Minnesota for an introductory statistics course. All of the activities, lesson plans, and data are available at http://www.tc.umn.edu/~aims/index.htm
- Challenges: Motivation, acceleration and attitude associated with this for students, maturity, isolation and social issues, and not wanting to be moved outside of age group.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: (descriptive list) |
Teachers are: (descriptive list) |
|
thinking logically. |
structuring class activities for discussion, justification, and exploration. |
|
posing questions. |
questioning student ideas. |
|
hypothesizing about possible outcomes. |
having students refine or revise their thinking or work. |
|
choosing tools and methods of inquiry. |
providing or allowing students to find relevant data for students to investigate. |
|
designing or changing representations. |
helping students see major concepts, big ideas and general principles and not merely having students engage in isolated facts. |
|
interpreting results. |
helping students connect new information to prior knowledge. |
|
drawing conclusions and justifying them. |
letting students build on each other's ideas. |
|
investigating real world problems which allow for many interactions and collaboration in the classroom. |
allowing multiple conclusions drawn from data, if those conclusions are supported statistically by the students. |
|
technology is being used to contribute to making sense of data and constructing meanings of basic statistical concepts as well as to facilitate the use of multiple data representations. (ben-Zvi, 2009). |
using correct language when discussing statistics, while pointing out the common misuses of terms/ideas. |
|
using logical arguments to support their conclusions. |
|
Parent Resources
Parents can discuss statistical graphs or information presented in the newspaper or other media with their children. Parents can ask their children what the graphs or analysis means, what information is not included that might be helpful, what conclusions are supported by the data, and what are the limitations of the statistics presented.
- Lohr, S. (2009). For today's graduate, just one word: Statistics. New York Times. This is an article about the growing variety of jobs in statistics that are available due to the advancements in technology.
- National Library of Virtual Manipulatives. This website has a variety of applets and activities for students to explore patterns and investigate probability.
- High School Statistics Resources for Teachers, Parents, and Students. This website has summary information of other websites that can be helpful for further information, practice, and exploration for students.
- ChanceWiki This website has a variety of real-world uses and misuses of statistics. It is maintained by Dartmouth College.
- Search Youtube or Video Google for instructional videos on probability and statistics.