9.3.3B Triangles
Know and apply properties of equilateral, isosceles and scalene triangles to solve problems and logically justify results.
For example: Use the triangle inequality to prove that the perimeter of a quadrilateral is larger than the sum of the lengths of its diagonals.
Overview
Standard 9.3.3 Essential Understandings
The study of geometric figures might be considered one of the "main topics" in geometry, along with, among others, proportional thinking, reasoning and sense making. The focus of this standard is on geometric figures, with the others listed above also being involved to a great extent.
In this standard, students will work with a transversal that intersects two lines. They will study angles formed by the three lines, and determine whether or not the two intersected lines are parallel. They will see many types of triangles, including "special" triangles such as isosceles, equilateral, right, 30-60-90 and 45-45-90 triangles, focusing on the properties of each of these figures.
Students will study similarity and understand that congruence is a special case of similarity. They will work with scale factors in "real-life" applications of similar figures. They will look at quadrilaterals and put them into a hierarchy, with "special" quadrilaterals being "nested" within others. Also, in this standard, students will study circles and their properties, with special focus on their applications.
Benchmarks Group B - Triangles
9.3.3
9.3.3.3 Know and apply properties of equilateral, isosceles and scalene triangles to solve problems and logically justify results.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Compare and contrast properties of scalene, isosceles and equilateral triangles.
- Work with the properties of these triangles in order to solve problems.
Work from previous grades that supports this new learning includes:
- Know definitions of isosceles triangle, scalene triangle and equilateral triangle.
NCTM Standards
Geometry
- Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships:
- Analyze properties and determine attributes of two- and three-dimensional objects;
- Explore relationships (including congruence and similarity) among classes of two- and three-dimensional geometric objects, make and test conjectures about them, and solve problems involving them;
- Establish the validity of geometric conjectures using deduction, prove theorems, and critique arguments made by others;
- Use trigonometric relationships to determine lengths and angle measures.
- Use visualization, spatial reasoning, and geometric modeling to solve problems:
- Use geometric models to gain insights into, and answer questions in, other areas of mathematics;
- Use geometric ideas to solve problems in, and gain insights into, other disciplines and other areas of interest such as art and architecture.
Common Core State Standards (CCSM)
- HS.G-CO (Congruence) Prove geometric theorems.
- HS.G-CO.9. Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment's endpoints.
- HS.G-CO.10. Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point.
- HS.G-CO.11. Prove theorems about parallelograms. Theorems include: opposite sides are congruent, opposite angles are congruent, the diagonals of a parallelogram bisect each other, and conversely, rectangles are parallelograms with congruent diagonals
- HS.G-SRT (Similarity, Right Triangles, & Trigonometry) Define trigonometric ratios and solve problems involving right triangles.
- HS.G-SRT.7. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures.
- HS.G-SRT (Similarity, Right Triangles, & Trigonometry) Apply trigonometry to general triangles.
- HS.G-SRT.10. Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
- HS.G-C (Circles) Understand and apply theorems about circles.
- HS.G-C.1. Prove that all circles are similar.
- HS.G-C.2. Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.
- HS.G-C.3 Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle.
- HS.F-TF (Trigonometric Functions) Extend the domain of trigonometric functions using the unit circle.
- HS.F-TF.3. Use special triangles to determine geometrically the values of sine, cosine, tangent for π/3, π/4 and π/6.
Misconceptions
- Students might confuse the different types of triangles as they are defined by their sides.
- Students might incorrectly apply or transfer properties from one type of triangle to a different type.
Vignette
In the Classroom
This vignette explores different types of triangles and their angles.
Teacher: Today, we're going to look at different types of triangles. One way to classify triangles is by their sides. If that's what we're looking at, what types of triangles are there?
Student 1: I know that an equilateral triangle has all its sides congruent.
Teacher: Right. What else?
Student 2: An isosceles triangle has two sides congruent.
Teacher: Yes, and in our definition, we'll say that it has AT LEAST two sides congruent.
Student 2: So does that mean that an equilateral triangle is a special type of isosceles triangle?
Teacher: Very good. You're right.
Student 3: A scalene triangle has no congruent sides.
Teacher: Right. How about if we classify triangles by their angles?
Student 4: A right triangle has one right angle.
Teacher: Yes, it does. Could it ever have two right angles?
Student 4: No, because that would mean that the two angles would have a sum of 180, and that's the sum of the measures of all three angles of a triangle.
Teacher: Right. What else?
Student 5: An obtuse triangle has one obtuse angle, and that's all it could have, for the same reason that a right triangle could have only one right angle.
Teacher: You're correct. What other types of triangles are there?
Student 6: An acute angle has three acute angles.
Teacher: Good.
Student 7: An equiangular triangle has three congruent angles. This is also an acute triangle, because the measure of each angle must be 60.
Source: This activity comes from the National Council of Teachers of Mathematics (NCTM). It is titled "Triangle Classification" and is found on NCTM's Illuminations website. To find this activity on the Internet, click on the link below.
Resources
Teacher Notes
- Clearly differentiate between types of triangles.
- Clearly differentiate between properties of the different types of triangles.
Isosceles triangles PowerPoint
Equilateral triangles PowerPoint and video
Additional Instructional Resources
National Council of Teachers of Mathematics (NCTM). (2010). Focus in High School Mathematics: Reasoning and Sense Making in Geometry. Reston, VA: National Council of Teachers of Mathematics.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What other instructional strategies can be used to engage students with properties of triangles?
- How can manipulatives be used to help students visualize these abstract concepts?
- How can the instruction be scaffolded for students?
- What additional scaffolding should be provided to ELL students?
- Do the tasks that have been designed connect to underlying concepts or focus on memorization?
- How can it be determined if students have reached this learning goal?
- How can the lesson be differentiated?
Assessment
The teacher puts a diagram similar to the one below on the chalkboard, SmartBoard, overhead, or interactive geometry software.

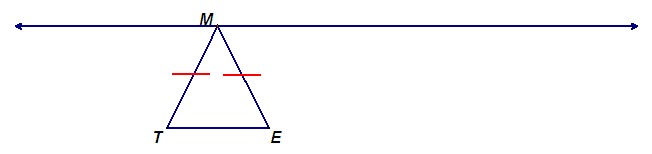
Teacher: Where, on this line, could you put a point M so that triangle MTE is isosceles?
Student 1: I know - right above the middle of the segment, like this.
Student draws on the board:
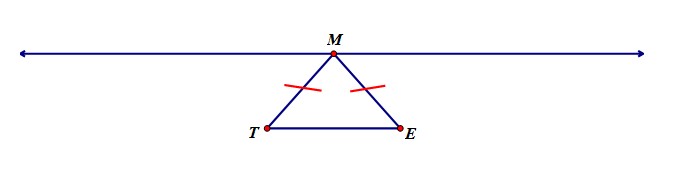
Teacher: Great. Are there any other possibilities?
Student 1: No, I don't think so, because that's the only place where segment MT is congruent to segment ME.
Student 2: But do those have to be the congruent segments?
Teacher: What do you mean?
Student 2: Well, we could put point M somewhere else, so that segment TE is congruent to segment ME.
Teacher: Could you show that on the board?
Student 2 puts the following on the board:
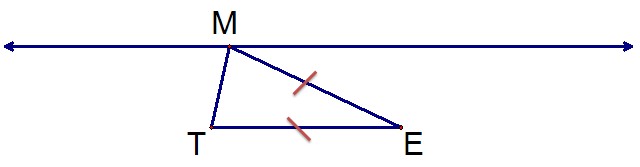
Teacher: That's a good thought. Are there any other places M could go on the line?
Student 3: Well, there is another pair of sides we could have congruent.
Teacher: What other pair?
Student 3: The only other pair that we haven't used yet would be to have segment MT be congruent to segment TE.
Teacher: Would you show that on the board?
Student 3: Sure.
Teacher: So, that's three places. Are there any others?
Student 3: I don't think so, because we have used up all the different pairs of congruent sides.
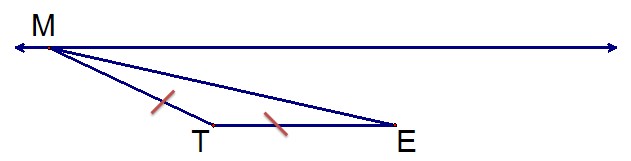
Student 4: How about if we put M on the other side?
Teacher: What do you mean? Which other side?
Student 4: On the other side of the first point - the same situation as the second and third spots, but to the right instead of to the left.
Teacher: Could you show that?
Student 4: Like this:
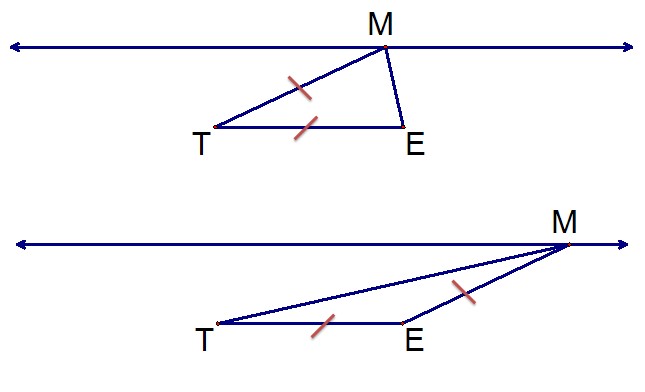
Teacher: So that gives us five different places where we could place point M in order to have triangle MTE be isosceles. Are there any others?
Student 5: I don't think so. I think there are only five.
Teacher: Would there always be five points on that line that would make triangle MTE isosceles?
Student 5: Yes.
Student 6: Wait. What if segment TE was really short or really far away from the line?
Teacher: How would that affect the answer to the question?
Student 6: Well, if it looked like this...
Student 6 puts the following diagram on the board:
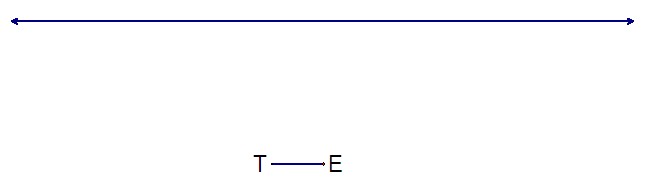
... then you couldn't have any point M on the line that would make segment ME congruent to segment TE, and you couldn't put any point M on the line to make segment MT congruent to segment TE.
Teacher: Very good. So, in this case, how many points are possible?
Student 3: Just one.
Teacher: What would it look like?
Student 3: Like this:
Student 3 places point M on the line:
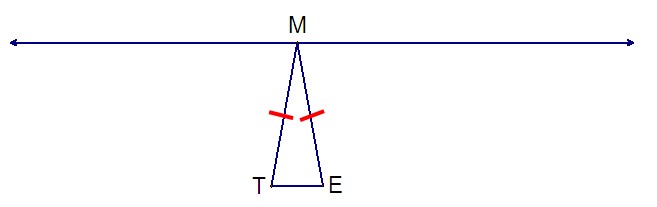
Teacher: Are there any other possibilities with any different segments?
Student 7: How about if the segment was the same size as the distance it is from the line?
Student 2: I can't get a picture of that in my head. Could you put it on the board?
Student 7: Yes.
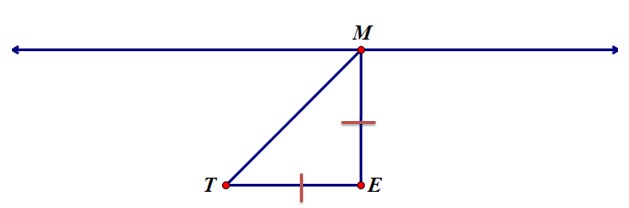
Teacher: OK, so if the diagram looks like that, how many points are possible on the line that would make an isosceles triangle?
Student 7: I think there are three: This point; the same thing on the other side, directly above point T; and the point in the middle. The other two look like this:
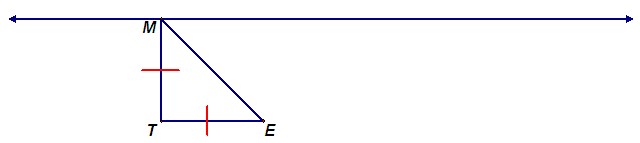
Differentiation
This Framework's assessment activity may need to be broken into two parts and done on two days.
Be careful not to proceed too quickly from one activity to the next. Also, watch vocabulary and do some type of verbal assessment from time to time.
Use the problem from this Framework's vignette (National Council of Teachers of Mathematics (NCTM) "Triangle Classification" activity can be found on NCTM's Illuminations website). The "Extensions" part of the NCTM Illuminations activity asks, "What is the probability that a random point C chosen on the plane will form an acute triangle ABC?" The answer will surprise people.
Parents/Admin
Students are: (descriptive list) | Teachers are: (descriptive list) |
working to place a "third vertex" of a triangle, given the first two vertices, in order to make a triangle that is isosceles, equilateral, scalene, right, obtuse or acute. | leading discussions on triangles. |
calculating the number of possible isosceles triangles, given a segment and a line parallel to it. | observing student work and asking probing questions to cause students to reflect on their mathematical learning. |
analyzing isosceles triangles, in particular how to form them given a segment and a line parallel to it. | engaging students in exploring and problem solving with triangles either with computer generated representations or hand drawn models. |
using various modes (chalkboard, SmartBoard, overhead projectors, or interactive geometry software) to represent triangular situations. | giving hints/suggestions when appropriate to scaffold student learning. |
Parent Resources
- Sophia geometry lessons
This social learning community website includes lessons on multiple topics. Most of these lessons were developed by teachers and reviewed.
- Khan Academy geometry lessons
This website offers a library of videos and practice exercises on multiple topics.
- Teacher Tube, YouTube
These websites include multiple uploaded lessons on most school topics.
- Mathematics textbooks
Many textbook publishers have websites with additional resources and tutorials. Check your child's textbook for a weblink.
