8.2.1 Linear & Nonlinear Functions
Understand that a function is a relationship between an independent variable and a dependent variable in which the value of the independent variable determines the value of the dependent variable. Use functional notation, such as f(x), to represent such relationships.
For example: The relationship between the area of a square and the side length can be expressed as f(x)=x2. In this case, f(5)=25, which represents the fact that a square of side length 5 units has area 25 units squared.
Use linear functions to represent relationships in which changing the input variable by some amount leads to a change in the output variable that is a constant times that amount.
For example: Uncle Jim gave Emily $50 on the day she was born and $25 on each birthday after that. The function f(x)=50+25x represents the amount of money Jim has given after x years. The rate of change is $25 per year.
Understand that a function is linear if it can be expressed in the form f(x)=mx+b or if its graph is a straight line.
For example: The function f(x)=x2 is not a linear function because its graph contains the points (1,1), (-1,1) and (0,0), which are not on a straight line.
Understand that an arithmetic sequence is a linear function that can be expressed in the form f(x) = mx+b, where x = 0, 1, 2, 3,....
For example: The arithmetic sequence 3, 7, 11, 15, ..., can be expressed as f(x) = 4x + 3.
Understand that a geometric sequence is a non-linear function that can be expressed in the form f(x) = abx, where
x = 0, 1, 2, 3,....
For example: The geometric sequence 6, 12, 24, 48, ... , can be expressed in the form f(x) = 6(2x).
Overview
Standard 8.2.1 Essential Understandings
Student learning is focused on the concept of function. Students must explore linear and non-linear functions to understand the relationship between the independent and dependent variables. This idea of every input having exactly one output is essential. Students must understand that changing the input leads to a change in the output. Linear and non-linear relationships should not be new learning for students. As 6th graders, students have been exposed to different types of patterns and explored ways to write rules for these patterns. In 7th grade, the focus moved to proportional linear functions and the equation y = mx. In 8th grade, they extend this learning to other linear and non-linear functions. However, they have not made the connection between equations of functions and function notation. It is important for students to make the connection that function notation is another way to write the linear and non-linear equations that they have already studied. Students will deepen their knowledge of function as they explore arithmetic and geometric sequences. The connecting of arithmetic sequences to linear functions as well as geometric sequences to exponential functions is crucial here. Ultimately, this standard focuses on students using and identifying functions and function notation.
All Standard Benchmarks
8.2.1.1
Understand that a function is a relationship between an independent variable and a dependent variable in which the value of the independent variable determines the value of the dependent variable. Use functional notation, such as f(x), to represent such relationships.Example: The relationship between the area of a square and the side length can be expressed as f(x) = x2. In this case f(5) = 25, which represents the fact that a square of side length 5 units has area of 25 units squared.
8.2.1.2
Use linear functions to represent relationships in which changing the input variable by some amount leads to a change in the output variable that is a constant times that amount.Example: Uncle Jim gave Emily $50 on the day she was born and $25 on each birthday after that. The function f(x) = 50 + 25 x represents the amount of money Jim has given after x years. The rate of change is $25 per year.
8.2.1.3
Understand that a function is linear if it can be expressed in the form f(x) = mx + b or if its graph is a straight line.Example: The function f (x) = x2 is not a linear function because its graph contains the points (1,1), (-1,1) and (0,0), which are not on a straight line.
8.2.1.4
Understand that an arithmetic sequence is a linear function that can be expressed in the form f(x) = mx + b, where x = 0, 1, 2, 3,....Example: The arithmetic sequence 3, 7, 11, 15, ..., can be expressed as f(x) = 4x + 3.
8.2.1.5
Understand that a geometric sequence is a non-linear function that can be expressed in the form f(x) = abx, where x = 0, 1, 2, 3,....Example: The geometric sequence 6, 12, 24, 48, ... , can be expressed in the form f(x) = 6(2x).
8.2.1.1
Understand that a function is a relationship between an independent variable and a dependent variable in which the value of the independent variable determines the value of the dependent variable. Use functional notation, such as f(x), to represent such relationships.Example: The relationship between the area of a square and the side length can be expressed as f(x) = x2. In this case f(5) = 25, which represents the fact that a square of side length 5 units has area of 25 units squared.
8.2.1.2
Use linear functions to represent relationships in which changing the input variable by some amount leads to a change in the output variable that is a constant times that amount.Example: Uncle Jim gave Emily $50 on the day she was born and $25 on each birthday after that. The function f(x) = 50 + 25 x represents the amount of money Jim has given after x years. The rate of change is $25 per year.
8.2.1.3
Understand that a function is linear if it can be expressed in the form f(x) = mx + b or if its graph is a straight line.Example: The function f (x) = x2 is not a linear function because its graph contains the points (1,1), (-1,1) and (0,0), which are not on a straight line.
8.2.1.4
Understand that an arithmetic sequence is a linear function that can be expressed in the form f(x) = mx + b, where x = 0, 1, 2, 3,....Example: The arithmetic sequence 3, 7, 11, 15, ..., can be expressed as f(x) = 4x + 3.
8.2.1.5
Understand that a geometric sequence is a non-linear function that can be expressed in the form f(x) = abx, where x = 0, 1, 2, 3,....Example: The geometric sequence 6, 12, 24, 48, ... , can be expressed in the form f(x) = 6(2x).
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Use function notation to represent linear relationships;
- Understand that x is the input and f(x) is the output. Changing the input changes the output in a specific way;
- Recognize and write a linear function (using function notation) to express arithmetic sequences;
- Recognize and write an exponential function (using function notation) to express geometric sequences;
- Recognize a linear function from a graph, table, or equation;
- Identify independent and dependent variables in real-life situations;
- Understand that there is a relationship between input and output ,and then represent this relationship in function notation;
- Understand that in order for a relationship to be a function, for every input there is only one possible output.
Work from previous grades that supports this new learning includes:
- Write an equation to represent two variables in a proportional relationship when given a situation, table or graph;
- Students are able to graph an equation;
- Understand that a proportional relationship is a straight line on a graph, the slope being the unit rate;
- Describe what happens to a graph when the unit rate is changed;
- Develop efficient, accurate, and generalizable methods for operating with rational numbers;
- Substitute an input value x into the function and calculate the output value f(x) for the function;
- Interpret proportional linear functions and determine slope from a table, graph, or equation.
NCTM Standards
Understand patterns, relations, and functions:
- Identify functions as linear or nonlinear and contrast their properties from tables, graphs, or equations;
- Represent and analyze mathematical situations and structures using algebraic symbols;
- Explore relationships between symbolic expressions and graphs of lines, paying particular attention to the meaning of intercept and slope;
- Use symbolic algebra to represent situations and to solve problems, especially those that involve linear relationships.
Analyze change in various contexts.
- Use graphs to analyze the nature of changes in quantities in linear relationships.
Common Core State Standards (CCSS)
8.F (Functions) Define, evaluate, and compare functions.
- 8.F.1 Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output.
- 8.F.3 Interpret the equation y = mx + b as defining a linear function, whose graph is a straight line; give examples of functions that are not linear. For example, the function A = s2 giving the area of a square as a function of its side length is not linear because its graph contains the points (1,1), (2,4) and (3,9), which are not on a straight line.
Misconceptions
Student Misconceptions and Common Errors
- Students sometimes consider an equations such as x = 10 a linear function. This is a linear equation, but it is not a linear function because there are infinite output values for the input value of 10.
- There is a misunderstanding about the notation f and f(x). The notation f is the name of the function (or rule) and f(x) is the output from the rule when x is the input.
- Students sometimes believe that f is the only letter that can be used to represent a function rule.
- In the form f(x) = mx+b, students sometimes switch the values and call m the y-intercept and b the slope.
- When students see f(x), the initially think it means f times x.
- When looking at a table of linear data where the x values are not increasing by a constant amount, students sometimes think the relationship is not linear because they think y is not changing by a constant amount, even though it is.
- When asked to write a linear function, students sometimes leave the equation as y =.
- Students sometimes will not understand why function notation is needed and think they can just use y= all the time instead of f(x).
- When trying to recognize the correct function notation for geometric sequences, sometimes students choose equations such as f(x)=4x2 because they see an exponent and think it is the right form.
- Students might confuse the vocabulary word range in this context with what they previously have learned about range being the difference between the maximum value and minimum value.
- A proportional relationship between two variables can always be modeled by a linear function, but not all linear functions represent proportional relationships.
Vignette
In the Classroom
In this vignette, students learn about functions through recalling what they know about function machines.
Teacher: How many of you remember learning about a function box or function machine? It may have looked something like this:
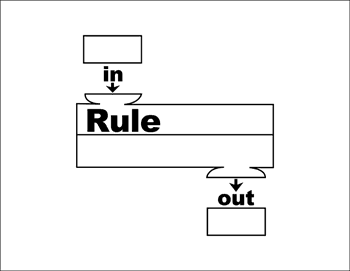
How did a function machine work?
Student: Well, we would put a number in and another number would come out.
Student: Sometimes we had to figure out which number would come out of the machine: sometimes they would give us what came out and we had to figure out what went in.
Teacher: Did you ever wonder why it was called a function machine?
When working with a function, for everything you put in you get exactly one thing out. Did you ever get more than output for each input when you were putting numbers through the function machine?
Student: No, I don't think so...
Student: But sometimes we were given the input and outputs and we had to figure out the rule.
Teacher: How did you figure out the rule?
Student: We would try to figure out the pattern and what we could do to all the "ins" to get the "outs" and make it always work.
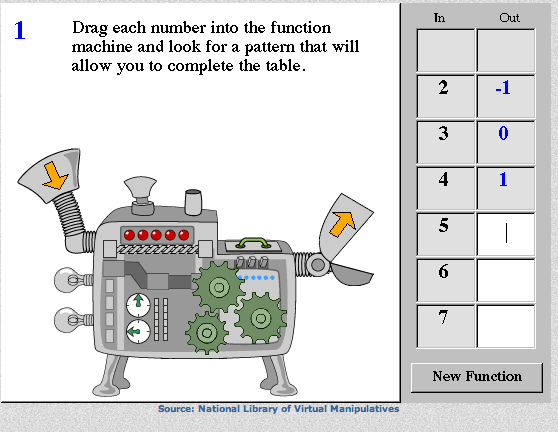
Teacher: What would be the rule for this function machine?
Student: That's easy. It's plus four.
Teacher: What does that mean?
Student: For every number you put in, add 4 and you will get the output.
Teacher: So in elementary school you focused on what the rule was for the function box. In middle school you continued to work with these function machines, but they were in the form of a table instead of a function machine.
How would you describe this relationship if it were a table of values?
x | y |
-1 | 3 |
2 | 6 |
5 | 9 |
Student: Well, it still adds four like the function machine, but we would write an equation for it like this: y = x + 4 .
Teacher: OK, so you have moved from writing a rule to writing an equation. They both mean the same thing. The equation is just more sophisticated because it represents all the possible values for that rule.
Student: Yeah. You can graph it and it will be a line that goes on forever. We could use the table to make tons of coordinate pairs using the equation.
Teacher: Next we need to move from writing equations to writing the relationship in function notation. So what does that mean?
Students: I'm not sure.
Teacher: Let's look at a few linear relationships written in function notation. What do you notice?
f(x) = 2x + 10
g(x) = -3x - 5
f(p) = 10 - 5p
h(s) = s - 4
Student: I notice that it looks a lot like the equations we wrote before, they just have that weird thing in the front with the letters instead of just a y. It looks much more confusing.
Student: I noticed that there is an x on both sides and another variable that looks like it is multiplying by that x.
Teacher: I'm glad you brought that up. In this case, those parentheses do not represent multiplication and the f is not another variable.
Let's check it out - f(x). You read this as "f of x," and g(x) as "g of x."
It means that 2x +10 is a function of x, and -3x - 5 is a function of g.
Student: So what does that mean? Why did you use different letters?
Teacer: The letters name the function. This is actually a helpful tool that makes functions a little more user-friendly. If we were comparing two functions, we could name them different names and then avoid saying "the first equation or the equation with a y-intercept of 12."
But we need to go back a minute. What does it mean to be a function? We talked about it earlier with our function machines.
Student: It means that if we put a value for x into 2x + 10, we will get one answer out.
Teacher: Let's try it. What number should we put in?
Student: 5.
Student: 2(5) + 10 = 20. So f(x) = 20? Why don't we just leave it as y and write y = 20? It's way easier.
Teacher: Well, we would actually write f(5) = 20. What do you think about that? What does that tell us about the function f(x) = 2x + 10?
Student: Cool. It looks like the x gets replaced with the number we put in. So then we know the input is 5 and 20 is the output. When we just use y, we don't know what was put in.
Teacher: Let's make a table of values to represent f(x) = 2x + 10.
The teacher gives students time to make the table.
x | f(x) = 2x + 10 | f(x) |
-2 | f(-2) = 2(-2)+10 | 6 |
-1 | f(-1)=2(-1)+10 | 8 |
0 | f(0) = 2(0)+ 10 | 10 |
1 | f(1) = 2(1)+10 | 12 |
2 | f(2) = 2(2)+10 | 14 |
Student: So I could write
For f(x) = 2x +10
f(-2) = 6
f(-1) = 8
f(0) = 10
And that helped me to see the input and the output. Now it's kind of like there is only one variable because f(x) is the same as y.
Teacher: So let's try a few.
Students make tables for the other three function examples above then share their answers and continue the function discussion.
Teacher: What if I gave you this arithmetic sequence instead? What do these numbers represent? 2, 6, 10, 14 . . .
Student: I think the numbers in the sequence would represent outputs. The position of the number is like the input. So if I put 1 in, I should get 2 out. If I put 2 in, I should get 6 out. If I put in 3, I should get out 10. Is that correct?
Teacher: Yes, good thinking! Now... write a function to represent this sequence.
Student: The rule looks like it adds 4 every time, but if 2 is the 1st number, then the "0" value has to be -2. The equation would be y = 4x - 2. So the function would be f(x) = 4x - 2? Let me try it. The second value is a 6 so if I input 2 I should get an output of 6.
f(2) = 4(2) - 2
f(2) = 6
It works!
Teacher: What if I had this sequence? 6, 18, 54, 162 . . .
What's the pattern? Can you write an equation? Can you write a function? Think about it and we will start with this pattern tomorrow.
Resources
Teacher Notes
- One situation where function notation is useful is when there is more than one function that you are referring to. For example, when asked to compare graphs or which function reaches 200 first, it is useful to have a name for each function (whether in table, graph or equation format) and have them labeled with f(x) or g(x). If the functions were defined both using "y=" we would be very unclear about distinguishing between them, using potentially ambiguous phrases such as "the first equation" or "the graph with the highest y-intercept."
- Point out another advantage to function notation: it provides shorter way of writing about the relationship. It is shorter to write if f(x) = 5x + 3, or to write then f(10) = ? than to write if y = 5x + 3 and to calculate the value of y when x is 10.
- Students need to know that a function is a relationship where every input has at most one output. Show what that would look like in table format and as a graph. Students should realize that one output for every input means that for a graph to represent a function, it must pass the vertical line test. If you draw a vertical line anywhere on the coordinate axis, the line must only pass through the graph once, at most. If the vertical line passes through the graph more than once, the relationship graphed is not a function. Therefore an equation of the form x = k is not a function. While it is a linear relationship, it is not a linear function. This analogy will help students understand the vertical line test: It is impossible to have a moving object be at two different places on the graph after the same amount of time.
- When writing function examples, teachers should be deliberate to change the letter used to represent the function and not always use f(x). Students need to realize that any letter can be used when representing a function using function notation.
- When transforming a geometric sequence to the form f(x) = abx, make sure students realize that the only type of equation that matches with geometric sequences have the variable x as an exponent.
- When teaching students about input and output, domain and range are often used when moving into talking about functions. Be clear that this idea of range is different from their past experience with range.
- Some textbooks refer to linear and non-linear functions, but the curriculum never uses function notation. It is important for students to know how to use function notation.
Guided practice and video of function problems
This lesson is designed to introduce students to the idea of functions composed of two operations, with specific attention to linear functions and their representations as rules and data tables, including the mathematical notions of independent and dependent variables.
Meat-a-morphosis: An introduction to functions
This video of created by students of an animated function machine gives a concrete example of an input-output relationship.
Secret code functions
A two-day lesson on using secret codes to introduce the concept of a function.
Function machine
This website has a game involving a function machine in which students need to predict the function.
input - independent variable - domain: the number or value that is entered into a function. This may also be referred to as the manipulated variable (the variable that the experimenter decides to change to see if there is or is not an effect).
output - dependent variable - range: the number or value that comes out from a process. For example, in a function a number goes in; something is done to it; and the resulting number is the output. This may also be referred to as the responding variable (the variable that will change as a result of the change in the manipulated variable. It may also be observed and or measured to determine the quantity or quality of change).
domain: the set of x-coordinates of the set of points on a graph; the set of x-coordinates of a given set of ordered pairs; the value that is the input in a function or relation.
range: the y-coordinates of the set of points on a graph; also, the y-coordinates of a given set of ordered pairs. The range is the output in a function or a relation.
function: a rule matching elements of two sets of numbers in which an input value from the first set has only one output value in the second set.
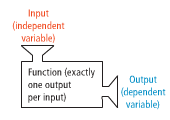
function notation: notation that uses the symbol f(x) in place of y; "f(x)" is read "f of x" and means that the value of the function (f(x) or y) depends on the input value of x; the function f(x) is the output of the function with input x.
Example:
"Find the value of y if y = x + 5 and x = -2" can be written in function notation as "find f(-2) if f(x) = x + 5."
If f(x) = -x2, then f(0) = 0, f(3) = -9, and f(-3) = -9.
arithmetic sequence: a sequence of numbers of the form a, a + b, a + 2b, a + 3b, ... , a + (n - 1)b. The sequence consists of a number that is constantly being added to each term to get the next term.
Example: 4, 7, 10, 13, 16, 19, 22, 25, ...
linear function: a function whose rule may be written in the form f(x) = mx + b where m and b are real numbers, m represents the slope, and b represents the y-intercept of the function. A linear function has a constant rate of change that results in a straight line graph.
geometric sequence: a sequence of numbers of the form a, ar, ar2, ar3,....., arn-1. Each term is being multiplied by a constant number to get the next term.
Example: 2, 4, 8, 16, 32, 64, ....
non-linear function: any function that does not follow a linear pattern of a constant rate of change, a straight line graph and an equation of the form f(x)=mx + b.
common difference: for an arithmetic sequence, the common difference is the difference between each term in the sequence.
Example: The sequence 3, 5, 7, 9, 11... is made by adding 2 each time, and so has a common difference of 2; there is a difference of 2 between each number.
exponential function: a function of the form y = a(bx)where a represents the y-intercept and b represents the growth factor (the number multiplied by).
common ratio: for a geometric sequence, the common ratio is the ratio of a term to the previous term; it is the number multiplied by in a geometric sequence.
Example: The geometric series 3, 6, 12, 24, 48, . . . has common ratio of 2.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- How can you help students connect what they already know about linear equations to their learning of linear function notation?
- How can the use of function machines support your teaching of linear and non-linear functions?
- Discuss ways to help students understand the purpose of function notation. Why would they use it?
Materials
- Lloyd, G., Beckmann, S., Zbiek, R.M., and Cooney, T. (2010) Developing Essential Understanding of Functions for Teaching Mathematics in Grades 9-12. Reston, VA: National Council of Teachers of Mathematics.
- Lloyd, G., Beckmann, S., Zbiek, R.M., and Cooney, T. (2010) Developing Essential Understanding of Functions for Teaching Mathematics in Grades 9-12. Reston, VA: National Council of Teachers of Mathematics.
- Cramer, K. (2001). Using Models to Build Middle-Grade Students' Understanding of Functions. In Mathematics Teaching in the Middle School 6(5), 310.
- Math Focal Point: Analyzing Linear Functions and Equations. (n.d.). NSDL Middle School Portal for Math and Science Teachers. Retrieved June 22, 2011, from http://msteacher.org/epubs/math/math16/linear.aspx
- Math Forum: Lines and Slope (Chameleon Graphing). (n.d.). The Math Forum @ Drexel University. Retrieved June 22, 2011, from http://mathforum.org/cgraph/cslope/
- Principles and standards for school mathematics. (2000). Reston, VA: National Council of Teachers of Mathematics.
- Schielack, J. F. (2010). Focus in grade 8: teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
- Secret Codes. (n.d.). Freaky Smart. Retrieved June 21, 2011, from designatedderiver.wikispaces.com/Secret+Codes
Assessment
1. You have returned some merchandise to a store and received a store credit of $22. In the same store, you are purchasing video games that cost $8 each. The function f (x) = 8x - 22 represents your total cost f (x) if you purchase x picture frames. How many dollars will you pay if you purchase 7 video games?
DOK Level: 1
Answer: $34
2.
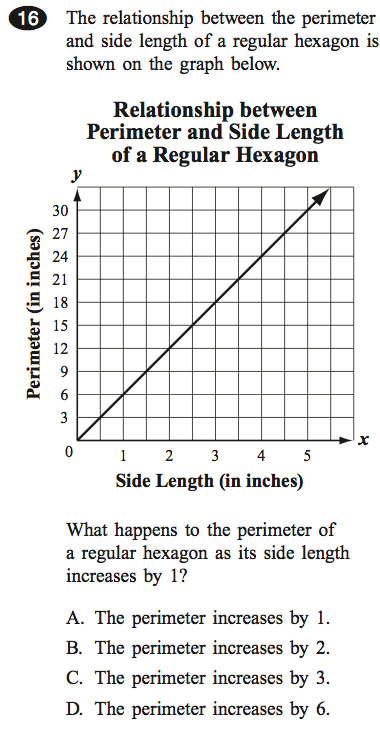
DOK Level: 2
Answer: D
Source: Massachusetts Comprehensive Assessment Released Exam
3. Which of the following represents a non-linear function?
a. f(x) = $\frac{4}{x}$
b. f(x) = $\frac{x}{7}$
c. g(x) = 2(x - 4)
d. g(x) = $\pi$x
DOK Level: 1
Answer: A
4. Find the formula for the nth term of the arithmetic sequence -7, -4, -1, 2, ...
a. f(n)= 3n - 4
b. f(n) = -7n + 10
c. f(n) = 3n - 10
d. f(n) = -7n + 4
DOK Level: 2
Answer: C
5. The following question refers to the graph shown below.
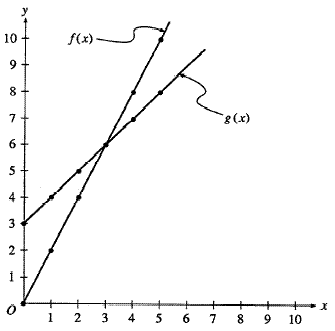
What is the value of g(1)?
1. 2
2. 4
3. 5
4. 6
5. 8
DOK Level: 2
Answer: 2
Source: Taken from NAEP
http://www.glencoe.com/sec/math/studytools/cgi-bin/msgQuiz.php4?isbn=0-02-825326-4&chapter=5&lesson=4&headerFile=6 a website with multiple choice questions relating to these benchmarks.
Differentiation
- Function machine
Have students use a function machine to investigate the relationship between input and output. - Students should develop a graphic organizer that includes examples and non-examples of linear function.
- Students should practice looking for patterns and extending sequences before transferring the sequences into function notation.
- Linear functions
This website includes an algebra lesson with explanations and examples on linear functions.
- Students could develop a Frayer Model for the different vocabulary words related to these benchmarks.
- Function machines
ELL students benefit from visual aids when learning. Have them work with function machines to understand the concept of input/output.
- Help students sort out the many definitions of the word "function." Intentionally discuss the definition and description of how the word is used in this mathematical context.
- Students could examine and simplify composite functions and composite function notation, such as f(g(x)).
- Students could examine other types of functions and compare/contrast them to linear functions, such as exponential, quadratic and cubic functions.
- Students can look at piecewise functions.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) | Teachers are: (descriptive list) |
going back to what they know about linear relationships to help them understand linear function notation. | scaffolding student understanding by connecting to what they already know about linear and non-linear relationships. |
using function notation to represent situations. | using real situations to model the idea of functions. |
comparing arithmetic and geometric sequences and writing appropriate functions to match the sequences. | using what they know about function machines from previous grades. |
examining what happens to the output (y value) when the input (x value) changes a specific amount. | giving students opportunities to compare different linear functions in function notation. |
looking at functions graphically to determine if the given function is linear or non-linear. | defining a function using tables, graphs and equations. |
Parent Resources
- Identify a function
This website helps students learn how to identify a function by analyzing the domain and range and using the vertical line test.
