6.4.1A Sample Space
Determine the sample space (set of possible outcomes) for a given experiment and determine which members of the sample space are related to certain events. Sample space may be determined by the use of tree diagrams, tables or pictorial representations.
For example: A 6 x 6 table with entries such as (1,1), (1,2), (1,3), ..., (6,6) can be used to represent the sample space for the experiment of simultaneously rolling two number cubes.
Overview
Students begin with an intuitive sense of probability. The formal understanding of probability starts with determining the set of all possible outcomes of an experiment, or sample space. Describing this sample space in a visual representation (tree diagram, table, or picture) guides student thinking towards the relationship between an event and the entire sample space. The ratio between the size of the event and the size of the sample space becomes the foundation of probability at this level. Students use fractions, decimals, and percents to describe probability as a measure of certainty ranging from 0 to 1 inclusive. Students conduct experiments for events where the probability is known, to compare the experimental results (relative frequency) with expected probabilities. Other experiments are conducted in situations where no probabilities are known. The resulting experimental probabilities are then used to make predictions of what will occur in future experiments.
All Standard Benchmarks
6.4.1.1 Determine the sample space (set of possible outcomes) for a given experiment and determine which members of the sample space are related to certain events. Sample space may be determined by the use of tree diagrams, tables or pictorial representations.
6.4.1.2 Determine the probability of an event using the ratio between the size of the event and the size of the sample space; represent probabilities as percents, fractions and decimals between 0 and 1 inclusive. Understand that probabilities measure likelihood.
6.4.1.3 Perform experiments for situations in which the probabilities are known, compare the resulting relative frequencies with the known probabilities; know that there may be differences.
6.4.1.4 Calculate experimental probabilities from experiments; represent them as percents, fractions and decimals between 0 and 1 inclusive. Use experimental probabilities to make predictions when actual probabilities are unknown.
6.4.1.1 Determine the sample space (set of possible outcomes) for a given experiment and determine which members of the sample space are related to certain events. Sample space may be determined by the use of tree diagrams, tables or pictorial representations.
What students should know and be able to do [at a mastery level] related to these benchmarks.
Determine the set of all possible outcomes (sample space) for an experiment;
- Represent the set of possible outcomes using a variety of strategies, such as tree diagrams, organized lists, tables, and pictures;
- Use tree diagrams, tables, and pictures to determine the size of the sample space (number of possible outcomes);
- Use representations of a sample space to determine which members are related to certain events.
Work from previous grades that supports this new learning includes:
- Collect, display and interpret data using tables.
NCTM Standards
Understand and apply basic concepts of probability
○ Use proportionality and a basic understanding of probability to make and test conjectures about the results of experiments and simulations;
○ Compute probabilities for simple compound events, using such methods as organized lists, tree diagrams, and area models.
○ Recognize reasoning and proof as fundamental aspects of mathematics.
○ Make and investigate mathematical conjectures.
- Build new mathematical knowledge through problem solving.
- Create and use representations to organize, record, and communicate mathematical ideas.
- Use the language of mathematics to express mathematical ideas precisely.
- Recognize and apply mathematics in contexts outside of mathematics.
Common Core State Standards (CCSS)
7SP (Statistics and Probability) Investigate chance processes and develop, use, and evaluate probability models.
7.SP.5 Understand that the probability of a chance event is a number between 0 and 1 that expresses the likelihood of the event occurring. Larger numbers indicate greater likelihood. A probability near 0 indicates an unlikely event, a probability around 1/2 indicates an event that is neither unlikely nor likely, and a probability near 1 indicates a likely event.
7.SP.6 Approximate the probability of a chance event by collecting data on the chance process that produces it and observing its long-run relative frequency, and predict the approximate relative frequency given the probability. For example, when rolling a number cube 600 times, predict that a 3 or 6 would be rolled roughly 200 times, but probably not exactly 200 times.
7.SP.7 Develop a probability model and use it to find probabilities of events. Compare probabilities from a model to observed frequencies; if the agreement is not good, explain possible sources of the discrepancy.
7.SP.8 Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.
- 7.SP.8b. Represent sample spaces for compound events using methods such as organized lists, tables and tree diagrams. For an event described in everyday language (e.g., "rolling double sixes"), identify the outcomes in the sample space which compose the event.
Misconceptions
Student Misconceptions and Common Errors
- Students may incorrectly determine the size of sample space from tree diagrams. For example, students may infer from this tree diagram that an experiment with three coin tosses has 14 possible outcomes rather than 8;
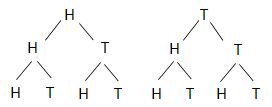
- In experiments involving combinations, students have trouble knowing when order matters and when it does not.
Vignette
In the Classroom
The following vignette shows students using a variety of strategies to determine sample space for an experiment that involves rolling two dice.
Mr. Xiong: I'm interested in knowing what strategies you used to determine the set of all possible outcomes for an experiment that involves rolling two dice. Who's willing to share?
Student: I am. I figured out all the possible outcomes by drawing a picture of the dice. Here's my picture.

First I drew all the possibilities that could happen if I got a one on the first roll. You can see them in the first row. Then I drew all the possibilities for rolling a two first. That's the second row. Then I did three, and so on. I found 36 different possibilities.
Mr. Xiong: Very nice, and well organized. Drawing a picture is one strategy that can be used to determine sample space, or the set of all possible outcomes. What other strategies can be used?
Student: I used a tree diagram.

The top row shows what I might get on the first roll, and the bottom row shows what I might get on the second roll.
Mr. Xiong: The picture strategy clearly shows 36 different outcomes. How can the tree diagram be used to identify those 36 outcomes?
Student: Well, you need to start at the trunk of the tree and follow all the branches. If you get a one on the first roll, you could get a one, two, three, four, five, or six on the second roll. That's six different possible outcomes for getting a one on the first roll. Doing the same thing for getting a two on the first roll will give you six more possible outcomes. If you continue doing that, you'll end up with 36 different possible outcomes just like the picture shows.
Mr. Xiong: So the tree diagram is just another way to show the sample space.
Student: I found the 36 different possible outcomes by making a list of ordered pairs.
Mr. Xiong: Tell me more about your strategy.
Student: I used the first number in the ordered pair to represent the first roll, and the second number in the ordered pair to represent the second roll. Here's a list of my ordered pairs.
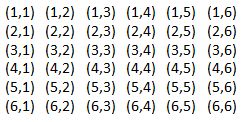
Student: Hey, that looks just like my picture!
Student: I got the same exact results by making a table!
Mr. Xiong: Please show us how you set up your table.
Student: I started by putting the possible results of the first roll down one side and the results of the second roll across the top. Then I filled in the table. The first number in each ordered pair shows the results of the first roll, and the second number shows the results of the second roll. My table looks like this.
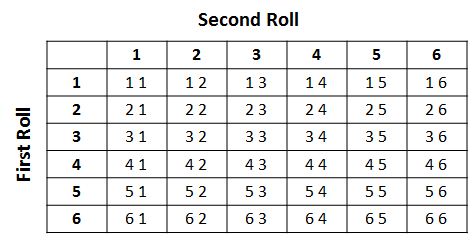
Mr. Xiong: Wow! I'm impressed! We already have four different strategies to determine the set of all possible outcomes for rolling two dice. I want you to take a few minutes now to use each of these four strategies, drawing a picture, making a tree diagram, listing ordered pairs, and making a table, to determine sample space in an experiment involving a coin toss and rolling a die.
Resources
- Students who incorrectly determine the size of sample space from tree diagrams will benefit from using other representations, such as organized lists or tables, to determine size of sample space.
- It is important to pose questions that require students to consider whether order matters. For example, in "Pick three colors from a box of crayons," the combination (red, yellow, blue) is considered the same outcome as (red, blue, yellow). However, in "Place three colored blocks in a stack," those two orderings would be considered different outcomes. It is important that students can make these distinctions in order to correctly determine the size of sample space.
- Increased understanding of sample space stems from multiple opportunities to determine and discuss possible outcomes and predict and test using simple experiments.
- Students benefit from multiple experiences with a variety of manipulatives, such as spinners, number cubes, coins, cards, and colored tiles.
- Connect new vocabulary to students' prior knowledge and experiences. For example, students may think of a birthday party as an "event" or special happening. A probability "event" can also be thought of as a special happening; e.g., drawing a red Jack from a deck of cards. Students may understand "outcome" by thinking of it as what "comes out" from one trial of an experiment.
- Students need support in creating and using representations to organize, record, and communicate their thinking. The use of multiple strategies to represent possible outcomes, such as tree diagrams, organized lists, tables, grids, and pictures will increase the likelihood of learning.
- Misaddressed, a challenge where a chart or tree diagram could be used to determine probability identifying whether checks have been placed in the correct envelopes.
Additional Instructional Resources
Exploring Probability - Explore It (Object Interactive), an interactive resource that allows students to explore outcomes resulting from tossing a coin, rolling a die, and using a spinner.
between 0 and 1 inclusive: all numbers from 0 to 1, including 0 and 1
combinations: groups
Example: A nickel, a dime, and a penny are a combination of coins.
event: collection of outcomes of a probability experiment. The outcomes in an event are a subset of the sample space, to which a probability can be assigned.
Example: One event when rolling a die is getting a 5 or 6.
The probability of this event is $\frac{2}{6}$ or $\frac{1}{3}$.
outcome: result of one trial of an experiment
Example: The outcome for one trial of an experiment that involves a die and a coin may be 6H.
probability: a number from 0 to 1 inclusive that indicates the likelihood of an event happening. If all outcomes in the sample space are equally likely (most often the case at this grade level), probability is determined by the ratio of the size of the event (number of possible outcomes in which the event occurs) to the size of the sample space (number of all possible outcomes). A common exception to the "equally likely" rule is a spinner, where there may be two or more outcomes that aren't equally likely.
Example: The probability of getting an even nunber when rolling the die is $\frac{3}{6}$.
This probability can also be written as $\frac{1}{2}$, 0.5 or 50%.
Random: not predictable with respect to individual outcomes
Example: Flipping a coin is a random process because the outcome of an individual flip cannot be predicted.
sample space; set of all possible outcomes of an experiment
Example: The sample space for tossing two coins is {HH, TT, HT, and TH}.
tree diagram: a graphic organizer used to list all possibilities of a sequence of actions
Example: Tree diagram for the sequence of two coin tosses:
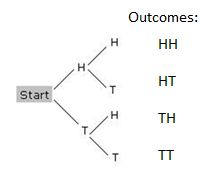
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- How were multiple approaches encouraged and modeled to solve problems?
- How were multiple representations of sample space encouraged and modeled?
- In what ways did students' existing knowledge of representing and displaying data build?
- Reflect on how teacher responses kept the focus on thinking and reasoning rather than only on getting the right answer.
Additional Materials
Details about these materials can be found in the References section.
Chapter 9, Probability, pp. 135-137.
(Click on "Uncertainty")
NCTM Principles and Standards for School Mathematics
Grades 6-8 Data Analysis and Probability, Understand and Apply, pp. 253-255.
NCTM A Research Companion to Principles and Standards for School Mathematics
Chapter 14, Research on Students' Understanding of Probability, pp. 216-224.
Keeley, P., & Rose, C. (2006). Mathematics curriculum topic study. Thousand Oaks, CA: Corwin Press.
Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
National Council of Teachers of Mathematics. (2010). Developing essential understanding of ratios, proportions & proportional reasoning Grades 6-8. Reston, VA: National Council of Teachers of Mathematics, Inc.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
Project 2061 Atlas of Science Literacy Volume 1. (2001). USA: American Association for the Advancement of Science.
Project 2061, Atlas of Science Literacy Volume 2. (2007). USA: American Association for the Advancement of Science.
Assessment
(DOK Level 1) (MCAS 2009 Mathematics released test item, Massachusetts Department of Elementary and Secondary Education, p. 181).
1. The tree diagram below shows all of the outfits Jay can choose to wear today. An outfit has one color of shirt, one color of pants and one color of shoes.
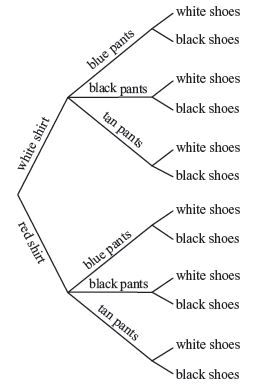
What is the total number of possible outcomes with a white shirt?
a. 9 b. 6 c. 3 d. 1
Answer: b
2. A baseball team has 4 pitchers and 3 catchers. How many pitcher-catcher combinations does the team have?
Answer: 12
(DOK Level 2)
3. List all the possible two-digit numbers that can be made using each of the digits 1, 2, 3 and 4 exactly once.
Answer: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43
(DOK Level 2) (MCAS 2008 Mathematics released test item, Massachusetts Department of Elementary and Secondary Education)
4. Ellen is ordering a new mountain bike. She must choose 1 option from each column in the table shown below.
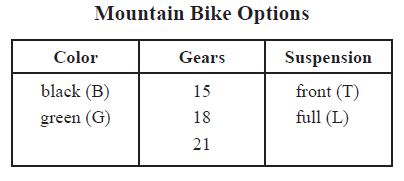
a. Show all possible ways Ellen can order her new mountain bike. You may use a tree diagram or an organized list.
Sample Answer:
(B, 15, T) (B, 15, L) (B, 18, T) (B, 18, L) (B, 21, T), (B, 21, L)
(G, 15, T) (G, 15, T) (G, 18, T) (G, 18, L) (G, 21, T) (G, 21, L)
b. What is the total number of ways Ellen can order a bike with a front suspension? Show or explain how you got your answer.
Sample Answer:
There are 6 ways to order a bike with front suspension. I counted how many of the total ways of ordering a bike included the front suspension.
(DOK Level 3) (SBA 2007 Mathematics released test item, Alaska Department of Education and Early Development, p. 9).
5. A player will spin each pointer one time while playing a game.
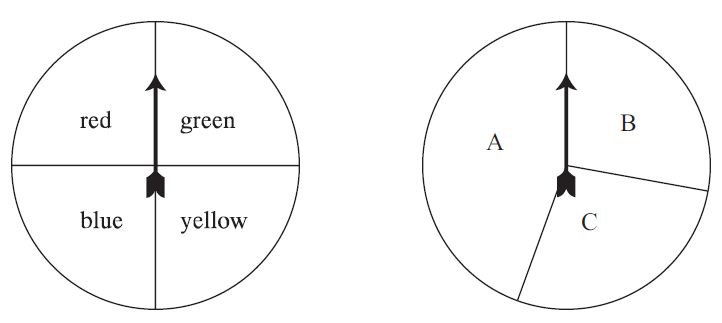
a. List all possible outcomes of one color and one letter.
Answer:
(Red, A), (Red, B), (Red, C), (Blue, A), (Blue, B) (Blue, C), (Yellow, A), (Yellow,B), (Yellow, C), (Green, A), (Green, B), (Green, C)
b. Explain why all of the possible outcomes are not equally likely.
Sample Answer:
The sections of the spinner on the right are not of equal size. The "A" section is larger than the "B" and "C" sections, so the outcomes are not equally likely.
(DOK 4)
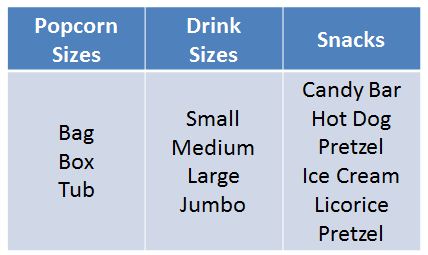
6. Use the chart below to create a menu for a movie theatre that results in 72 possible combinations of popcorn, drink, and snack.
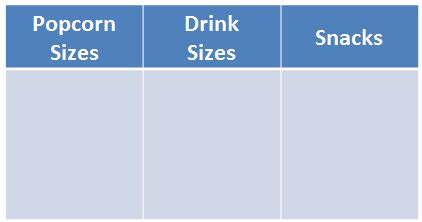
Sample Answer:
Differentiation
- Provide support for vocabulary development, such as use of graphic organizers and resource sheets;
- Use manipulatives such as spinners, number cubes, coins, and colored tiles to determine sample space;
- Use templates for data collection and teach strategies for recording and organizing data;
- Use scaffolding strategies to help students eventually develop their own tree diagrams, tables, and organized lists.
- Vocabulary words with multiple meanings, such as "heads," "tails," "tree" (diagram), "die," and (sample) "space" are problematic.
- Label pictures of pennies, nickels, dimes, and quarters with "heads" and "tails."
- Post and label examples of tree diagrams, including pictures of trees.
- The word "die" (singular) is problematic for all students. Post and label pictures of "die" (singular) and "dice" (multiple).
- "Sample space" is a new word for all students. Post pictures of experiments, with the set of all possible outcomes labeled as "sample space."
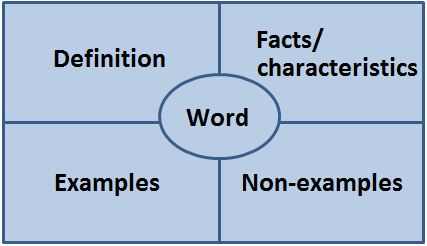
- Use graphic organizers such as the Frayer model shown below, for vocabulary development.
- Ask students to design an experiment with compound events that results in a certain number of outcomes.
Example: Molly designed an experiment involving a coin, a spinner, and a die. A tree diagram showing possible outcomes has 48 branches. What might Molly's experiment be?
Sample answer:
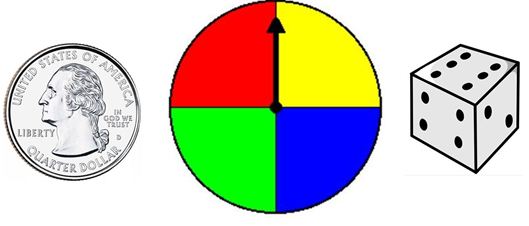
Molly's experiment included a coin toss, the spinner shown above, and a roll of the die. (2 x 4 x 6 = 48)
Parents/Admin
Students are: (descriptive list) | Teachers are: (descriptive list) |
using manipulatives, such as spinners, dice, coins, cards, and color tiles to determine the set of all possible outcomes. | modeling the use of a variety of manipulatives to determine the set of all possible outcomes. |
representing the set of all possible outcomes using a variety of strategies, such as tree diagrams, organized lists, tables, grids, and pictures. | modeling various strategies to represent the set of all possible outcomes. |
discussing various strategies for determining and representing all possible outcomes. | facilitating student conversations and posing questions that move students from concrete to visual to abstract representations. |
engaging in activities where they are asked to make conjectures about the size of sample space before determining its actual size. | asking students to make and test conjectures about the size of sample space for simple probability experiments. |
Exploring Probability - Explore It (Object Interactive), an interactive resource that allows students to explore outcomes resulting from tossing a coin, rolling a die, and using a spinner.
