6.2.2 Properties & Equivalent Expressions
Apply the associative, commutative and distributive properties and order of operations to generate equivalent expressions and to solve problems involving positive rational numbers.
For example: $\frac{32}{15}\times \frac{5}{6}=\frac{32\times 5}{15\times 6}=\frac{2\times 16\times 5}{3\times 5\times 3\times 2}=\frac{16}{9}\times \frac{2}{2}\times \frac{5}{5}=\frac{16}{9}$.
Another example: Use the distributive law to write: $\frac{1}{2}+\frac{1}{3}\left ( \frac{9}{2}-\frac{15}{8} \right )=\frac{1}{2}+\frac{1}{3}\times \frac{9}{2}-\frac{1}{3}\times \frac{15}{8}=\frac{1}{2}+\frac{3}{2}-\frac{5}{8}=2-\frac{5}{8}=1\frac{3}{8}$.
Overview
Standard 6.2.2 Essential Understandings
Students at this level begin to develop the ability to generalize numerical relationships and express mathematical ideas concisely using expressions and equations (e.g., three more than a number as x + 3, doubling as 2n, commutativity as a + b = b + a). Concrete models and pictorial representations of algebraic expressions are used to develop understanding that the commutative, associative, and distributive properties and order of operations apply in the same way that they did for numeric expressions. Students use these properties and the order of operations to generate equivalent expressions and evaluate expressions that involve positive rational numbers.
All Standard Benchmarks
6.2.2.1 Apply the associative, commutative and distributive properties and order of operations to generate equivalent expressions and to solve problems involving positive rational numbers.
Benchmark Group A
6.2.2.1 Apply the associative, commutative and distributive properties and order of operations to generate equivalent expressions and to solve problems involving positive rational numbers.
What students should know and be able to do [at a mastery level] related to this benchmark:
- Understand that algebraic expressions behave in the same way as numerical expressions;
- Apply the order of operations to generate equivalent numeric expressions involving rational numbers;
Examples: $12.6-(5.1+4.2)=12.6-9.3=3.3$; - Apply commutative, associative, and distributive properties to generate equivalent expressions;
Examples: $9 \times 52 = 9 \times (50 + 2) = (9 \times 50) + (9 \times 2) = 450 + 18 = 468$;
$12x + 2x = 2x + 12x = 14x$;
$5x \cdot 3 = 3(5x) = 15x$;
$(x + 2) \cdot 5 = 5(x + 2 ) = 5x + 10$; - Identify commutative, associative, and distributive properties used to generate equivalent numeric and algebraic expressions;
Examples: $3 \cdot (x+5) = (x+5) \cdot 3$; Commutative Property of Multiplication; - Evaluate algebraic expressions when given positive rational numbers as values for variables.
Work from previous grades that supports this new learning includes:
Apply the commutative, associative and distributive properties and order of operations to generate equivalent numerical expressions and to solve problems involving whole numbers;
- Determine whether an equation or inequality is true or false for a given value of the variable;
- Represent real-world situations using equations and inequalities involving variables. Create real-world situations corresponding to equations and inequalities;
- Evaluate expressions and solve equations involving variables when values are given for the variables.
NCTM Standards
Understand meanings of operations and how they relate to one another
- Understand the meaning and effects of arithmetic operations with fractions, decimals, and percents.
- Use the associate and commutative properties of addition and multiplication and the distributive property of multiplication over addition to simplify computations with integers, fractions, and decimals.
Common Core State Standards (CCSS)
6 EE (Expressions and Equations) Apply and extend previous understandings of arithmetic to algebraic expressions.
- 6.EE.3 Apply the properties of operations to generate equivalent expressions. For example, apply the distributive property to the expression 3(2 + x) to produce the equivalent expression 6 + 3x; apply the distributive property to the expression 24x + 18y to produce the equivalent expression 6(4x + 3y); apply properties of operations to y + y + y to produce the equivalent expression 3y.
Misconceptions
Student Misconceptions and Common Errors
- Students incorrectly apply the order of operations;
- Students may think that 3 x 5 is equivalent to 3 x 3 + 2, not recognizing the need for parentheses;
- Students misinterpret exponents (e.g., 42 as 4 x 2);
- Students may be confused by the differences between the commutative and associative properties and will incorrectly identify them;
- Since $2+\frac{1}{2}=2\frac{1}{2}$, students misinterpret 2x as 2 + x;
- Students do not recognize that x + x can be simplified to 2x;
- Students may misinterpret x + x + x as x3, rather than 3x;
- Students do not recognize that $x \cdot 5$ and $5x$ are equivalent expressions, resulting in the inability to generate the equivalent expression $8x$ for $x \cdot 5 + 3x$;
- When given x = 3, students incorrectly interpret 5x as 53.
Vignette
In the Classroom
In this vignette, students use associative, commutative, and distributive properties to generate equivalent algebraic expressions for the area of a rectangle.
Teacher: Today's task is to generate as many expressions as you can to represent the area of this rectangle.
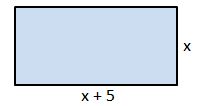
Teacher: To help us think about this, let's start by using algebra tiles to represent this rectangle.
Student1: I already drew a picture to show what that might look like.
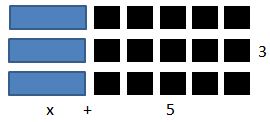
Teacher: What algebraic expression would you use to represent the area?
Student1: The picture shows x + x + x + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1.
Teacher: It certainly does. Is there another way to write that expression that may be a little simpler?
Student1: Sure. You could add all the (x)s together and add all the (1)s together. Then you'd get 3x + 15.
Teacher: So what you did was grouped the "like" terms. You put together all the (x)s in one group and all the (1)s in another group. We often use parentheses in mathematics to show groups, so you could write your work like this: (x + x + x) + (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1) = 3x + 15.
Student2: I know an easier way to do the problem.
Teacher: What would that be?
Student2: Well, I remember that the fastest way to find the area of a rectangle is to multiply the length by the width. That's why I wrote the area as x + 5 x 3.
Student3: I agree that the area of a rectangle can be found by multiplying the length by the width, but I think there's something wrong with your expression.
Teacher: Tell me more.
Student3: The algebra tiles show that there are 3 (x)s and 15 units. When you use the order of operations to simplify x + 5 x 3, you get x + 15. Somehow you lost two (x)s, but I don't know how.
Teacher: According to the order of operations, multiplication does come before addition so your observation is correct. How did the two (x)s get lost?
Student3: It's because you only multiplied the 5 by 3, and didn't multiply the x by 3.
Teacher: Oh, you're saying that 3 only got distributed over the 5 but not the x. How can we rewrite the expression to make it accurate and show that the 3 needs to get distributed, or multiplied by both 5 and the x?
Student3: You need to put parentheses around the x + 5.
Teacher: Show me what you mean.
Student3: Like this. (x + 5) x 3. That means that both the x and the 5 get multiplied by 3.
Teacher: Time out. I'm having a little trouble making sense of what you wrote, because you've used an x to represent the variable and an x to indicate multiplication. Is there another way to write the expression that may be a little less confusing.
Student3: I see what you mean. I suppose I could write the expression as (x + 5)٠3, since sometimes a dot is used to represent multiplication.
Student1: Why do you have to write any symbol at all?
Teacher: What are you suggesting?
Student1: That we write it like this: (x + 5)3.
Teacher: It is true that in algebra, when we write quantities right next to each other without any symbol in between, multiplication is implied. For example, 6y means 6 times whatever value the variable y has.
Student3: I understand that you're supposed to multiply when there's no symbol, but that expression looks confusing to me.
Teacher: What part is confusing you?
Student3: Writing the 3 at the end of the expression instead of the beginning.
Teacher: How do you suggest we write the expression?
Student3: I'd write 3(x + 5).
Teacher: Why is that less confusing to you?
Student3: Because we usually write the numbers first.
Teacher: Give me an example.
Student3: Like we usually write 3x, not x3.
Teacher: You do have a point. It is our practice in algebra to write the number that's being multiplied before the variable. But are those two expressions equivalent? Is 3x equivalent to x3?
Student3: I think so. If you substitute a number in for x, like 2, you get 6 for both expressions. In the first expression you multiply 3 times 2, and in the second expression you multiply 2 times three. You get the same thing. It's just that you multiply in a different order.
Teacher: Exactly. In mathematics we have a property that says that when you multiply, the order of the factors does not matter. You'll get the same result. It's the commutative property. Let's go back to our rectangle problem now. How are the expressions (x + 5)3 and 3(x + 5) different?
Student3: The only difference is the order that the factors are written down.
Teacher: Are the two expressions equivalent?
Student3: They must be.
Teacher: And how do you know?
Student3: Because of the commutative property.
Teacher: Yes, but remember - the commutative property only works for multiplication and addition. Subtraction and division are not commutative. If you change the order of the numbers when performing those operations you'll get different answers. Now I'm curious. Earlier we wrote the area of the rectangle as 3x + 15. How do we know that 3x + 15 and 3(x + 5) are equivalent?
Student1: Oh, that's another property. I think it's called the distributive property. You use that property to get rid of the parenthesis and simplify 3(x + 5).
Teacher: How does the distributive property work?
Student1: First you multiply 3 by x, which is 3x. Then you add 3 times 5, or 15. The answer is 3x + 15.
Teacher: The distributive property gets its name because it "distributes" the factor outside the parentheses over the terms within the parentheses. I know that properties are somewhat like laws; they always work. But why does the distributive property work?
Student1: I think it's sort of like using partial products.
Teacher: That's an interesting thought. The distributive property lets you "distribute," or multiply a number over each addend of a sum and then add the products. Let me give you an example of the distributive property using numbers.
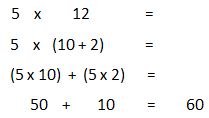
In this example the 5 is "distributed" to both the 10 and the 2. That means that 5 is multiplied by both 10 and 2, resulting in the partial products 50 (5 x 10) and 10 (5 x 2). When I add 50 and 10 together I get 60, which is the same result I get for 5 x 12 using any strategy. In our rectangle product, our partial products are 3x and 15. However, we're not able to combine them like we did with 50 and 10 because they're not "like" terms. But back to our original task of generating equivalent expressions for the area of the rectangle. So far we have:
x + x + x + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1
(x + x + x) + (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1)
3x + 15
(x + 5)3
3(x + 5)
We've also talked about how the commutative and distributive properties can be used to generate equivalent expressions. But I haven't heard anyone talk about the associative property. What is that property and how might it be used to generate an equivalent expression for the area of our rectangle?
Student1: The associative property is about grouping. It says that we can change the grouping of what's being added or multiplied without changing the results.
Teacher: Yes, and we often use parentheses to show those groups. Remember, this property does not apply to subtraction or division, just like the commutative property. So how can we use the associative property to find more equivalent expressions for the area of our rectangle?
Student1: I have an idea. I'm going to use the associative property to change the grouping of what's being added. Here's my thinking:
(x + x + x) + (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1) =
([x + x] + x) + ([1 + 1 + 1 + 1] + [1 + 1 + 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1]) =
2x + x + 4 + 11
That means that 2x + x + 4 + 11 is another expression for the area of the rectangle.
Teacher: Let's go back to our picture to verify that. I see 2 (y)s, another x, 4 ones, and 11 ones. The picture supports your idea. Now I'd like you to work with your partners to generate 3 more equivalent expressions for the area of the rectangle. Please identify which properties justify your thinking.
Resources
Teacher Notes
- The mnemonic Please Excuse My Dear Aunt Sally is helpful for students who cannot remember the order of operations (Parentheses, Exponents, Multiply, Divide, Add, Subtract). Remind students that calculations are always done left to right, and that groups must follow the rules working from innermost to outer.
- Students will benefit from a discussion of what the word equivalent means. For example, a dozen and 12 items, or $1.00 and 4 quarters are equivalent because they have the same value. In mathematics, we have equivalent fractions ($\frac{1}{2}$ and $\frac{2}{4}$) and equivalent measures (1 foot and 12 inches). Equivalent expressions, (12 + 7 and 7 + 12 or x + x + 2 and 2x + 2) also have the same value.
- Students who believe that 3 x 5 is equivalent to 3 x 3 + 2 need additional opportunities to see how parentheses are necessary to represent 5 as 3 + 2 and change the typical order of moving left to right when performing computations to maintain equivalence. They will benefit from activities where they are asked to insert parentheses into expressions to generate a given number. For example, how can parentheses be inserted into the expression 5 + 3 x 4 - 2 to make it equivalent to 30? Equivalent to 11? Equivalent to 15?
- Students' previous experiences with exponents has most likely been connected to place value using base 10; e.g. 102 = 10 x 10 = 100; 103 = 10 x 10 x 10 = 1000; 104 = 10 x 10 x 10 x 10 =10,000. Use this connection to help students see the base as a repeated factor, with the exponent telling how many times the base is repeated.
- The key words to remember are order for the Commutative Property and grouping for the Associate Property. Remind students that the Associative Property moves the parentheses but does not change the position of the numbers. The Commutative Property changes the positions of the numbers;
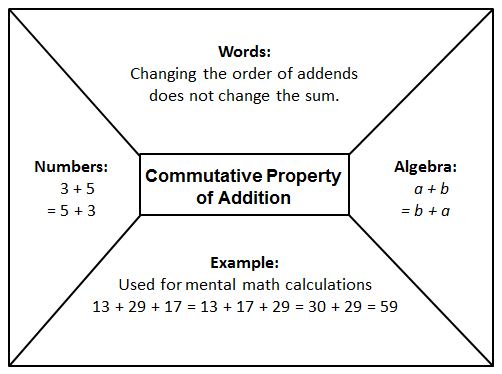
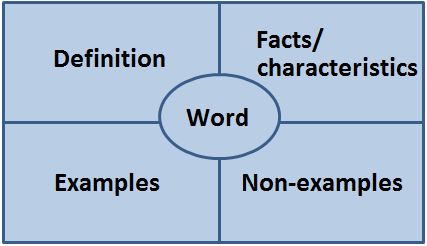
- Provide graphic organizers, such as those shown below, to help students understand the properties and how they are used to simplify numeric and algebraic expressions;
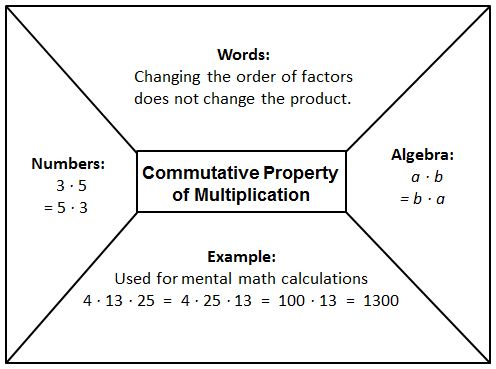
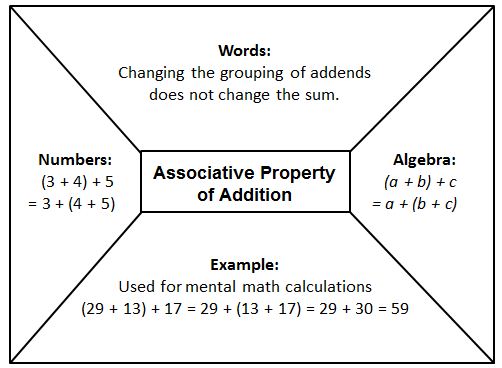
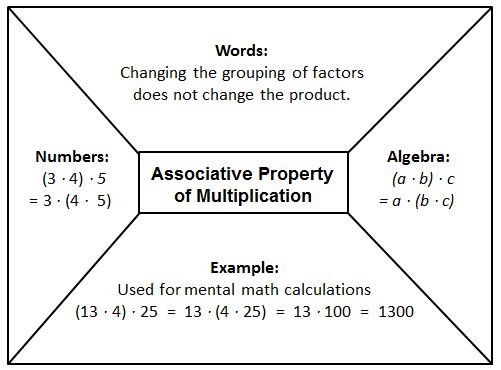
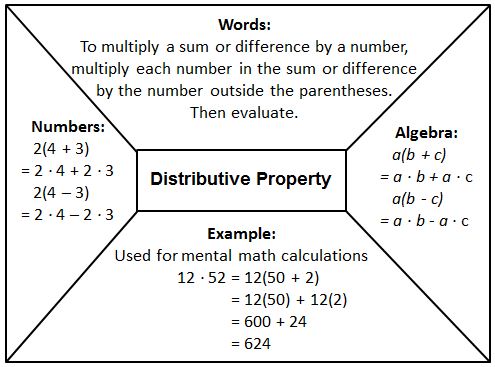
- Be sure to give students plenty of opportunity to use concrete materials and pictorial representations of algebraic expressions before moving to the symbolic. This will help students see that 2 + x is not equivalent to 2x , although $2+\frac{1}{2}=2\frac{1}{2}$.
- Without extensive concrete and semi-concrete experiences, it is also difficult for students to understand that x + x = 2x. Because the coefficient 1 is implied, students will benefit from the teacher writing the coefficient 1 whenever it is implied to make it explicit. Writing 1x + 1x + 1x may help students visualize three distinct quantities that can be added together and represented as 3x.
- The use of concrete models and pictorial representations will also help students who have the misconception that x + x + x can be expressed by the expression x3 rather than 3x. Remind students that in exponential notation, the base is a repeated factor, and does not indicate repeated addition.
- Students struggle to understand that x5 and 5x are equivalent expressions, because it conflicts with their previous experiences with numbers (53 and 35 are not equivalent). This provides an opportunity to show that the properties actually do act the same way with numbers and algebraic expressions. For example, 50 + 3 = 3 + 50 and 50 $\cdot$ 3 = 3 $\cdot$ 50 demonstrate the commutative property of addition and multiplication. In the algebraic expression x5, the multiplication is implied. Therefore, x5 means x $\cdot$ 5. According to the commutative property, x $\cdot$ 5 is equivalent to 5 $\cdot$ x, which is usually written as 5x. Therefore, x5 + 3x can be rewritten as 5x + 3x = 8x. In the number 53, the addition 50 + 3 is implied. According to the commutative property 53 = 50 + 3 = 3 + 50, not 35.
- Students that interpret 5x as 53 for x = 3 need to be reminded that in algebraic expressions when two quantities are written next to each other without any symbol, multiplication is implied. These students may benefit from discussion about how x is not usually used to represent multiplication in algebraic expressions to avoid confusion with the variable x, and that a dot is often used when a multiplication symbol is needed to prevent confusion.
Instructional Resources
Distributing and Factoring Using Area (NCTM Illuminations)
Additional Instructional Resources
This interactive website includes print activities with 5 different levels of difficulty.
This website is a game for two users where each player tries to connect four game pieces in a row before his or her opponent. Players can also choose game difficulty.
New Vocabulary
base (of an exponent): the number used as the factor in exponential notation baseexponent
Example: In 64 = 6 x 6 x 6 x 6, 6 is the base used as a factor 4 times.
exponent: in exponential notation (baseexponent ), the exponent is the number that tells how many times the base is used as a factor
Example: In 8 x 8 x 8 = 83, the exponent is 3 with base 8.
evaluate: to find the value. To evaluate algebraic expressions, particular numbers are substituted for variables before calculating.
Example: To evaluate 7x for x = 5, x is replaced with 5, resulting in 35
order of operations: the rules describing what sequence to use in evaluating expressions. All calculations are done left to right, in the following order:
- Parentheses and other grouping symbols; work from the innermost set using rules 2-4;
- Exponents
- Multiply or divide in the order the operations occur.
- Add or subtract in the order the operations occur.
Example: ${5}^{2}+(3\times 4-2)\div 5 = {5}^{2}+(12-2)\div 5$
$\; ={5}^{2}+\; \; \; \; 10\; \; \; \; \div 5$
$\; =25+\; \; \; \; 10\; \; \; \; \div 5$
$\; =25+\; \; \; \; \; \; \; \; \; \; 2$
$\; =27$
rational number: any number that can be expressed in the form $\frac{a}{b}$, where a and b are integers and b ≠0. A rational number can always be represented by either a terminating or a repeating decimal. Examples: $\frac{2}{3}$; 4 (which can be expressed as $\frac{4}{1}$); 2.25 (which can be expressed as $\frac{225}{100}$.)
simplify (an expression): to rewrite by removing parentheses and by combining like terms. Examples: 3x + 4 + 2 + 2x can be simplified as 5x + 6 and 3(2y + 4) - y can be simplified as 5y + 12
simplify (a fraction): to express in simplest form, or lowest terms. The numerator and denominator of proper fractions in simplest form have no common factor other than 1. Improper fractions and mixed numbers are in simplest form when the fraction part is proper and in simplest form. Examples: The numerator and denominator of $\frac{4}{8}$ share the common factor 4, so must be rewritten as $\frac{1}{2}$ to be in simplest form; $\frac{19}{3}$ written in simplest form is $6\frac{1}{3}$.
variable: a quantity that changes or that can have different values; a letter if often used to represent a variable quantity. Example: In the expression 5n, n is a variable because it can have different values.
Reflection - Critical questions regarding the teaching and learning of this benchmark:
How can concrete models and pictorial representations be used to move students to abstract representations?
- What activities will help students gain the understanding that algebraic representations work in the same way as numerical expressions?
- What evidence shows that students can apply and identify properties used to generate equivalent expressions?
- What evidence shows that students can apply the order of operations to generate equivalent expressions?
- What student misconceptions need to be addressed?
Materials - suggested articles and books
● Welder, R.M., Improving Algebra Preparation: Implications from Research on Student Misconceptions and Difficulties. Web. 01 May 2011.
● This article from NCTM's Principles and Standards for School Mathematics discusses the importance of using informal explorations with physical models, data, graphs, and other mathematical representations rather than facility with formal algebraic manipulation at the middle school level.
Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
Focus in Grade 6 Teaching with Curriculum Focal Points. (2010). Reston, VA: National Council of Teachers of Mathematics, Inc.
Developing Essential Understanding of Ratios, Proportions & Proportional Reasoning Grades 6-8. (2010). Reston, VA: National Council of Teachers of Mathematics, Inc.
Principles and Standards for School Mathematics. (2000). Reston, VA: National Council of Teachers of Mathematics, Inc.
Assessment
(DOK Level 1)
- Evaluate $\frac{2}{3}x+\frac{1}{2}$ for $x=\frac{3}{4}$.
Answer: 1
(DOK Level 1)
- Tell which property is illustrated by each statement.
a) $2.1 \cdot (m + 3) = (m + 3) \cdot 2.1$
b) $2.1 \cdot (m \cdot 3) = (2.1 \cdot m ) \cdot 3$
c) $2.1 \cdot (m + 3) = 2.1 \cdot m + 2.1 \cdot 3$
Answers:
a) commutative property of addition
b) associative property of multiplication
c) distributive property
(DOK Level 2)
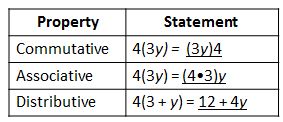
- Use the indicated property to complete each statement.
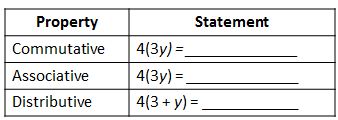
Answer:
(DOK Level 2)
- Simplify: 5m + 12 + 3(m + 2)
Answer: 5m + 12 + 3(m + 2) = 5m + 12 + 3m + 6 = 8m + 18
(DOK Level 3)
- Draw models for 2y + 4 and 2(y + 4). Explain how they are different.
Sample Answer:
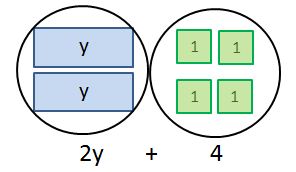
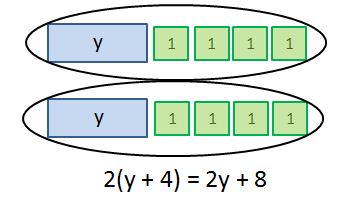
The model for 2y + 4 shows 2 (y)s and 4 ones. The model for 2(y + 4) shows two groups of y and 4 ones, which is the same as 2 (y)s and 8 ones.
(DOK Level 4)
- Sam says that 5m + 12 + 3(m + 2) is equivalent to 8m + 18. Prove Sam's statement by using the commutative, associative, and distributive properties. Identify each property used.
Sample answer:
5m + 12 + 3(m + 2) = 5m + 12 + 3m + 6 (Distributive Property)
= 5m + 3m + 12 + 6 (Commutative Property of Addition)
= (5m + 3m) + (12 + 6) (Associative Property of Addition)
= 8m + 18
Differentiation
Struggling Students
- Always provide algebra tiles or other manipulatives for students to make concrete representations of algebraic expressions.
- Provide graphic organizers, such as those shown below, to help students understand the properties and how they are used to simplify numeric and algebraic expressions.





This website is an interactive game where students practice order of operations and fluency with whole number facts.
This website provides students with practice identifying four properties that involve addition: commutative, associative, additive identity, and distributive.
This website provides students with practice identifying four properties that involve multiplication: commutative, associative, multiplicative identity, and distributive.
- Numbers always behave in the same predictable way. Help students understand that the sets of rules that describe how numbers behave are referred to as Properties in mathematics. How the numbers are behaving can help identify which property is being used. Make students aware that the word property has multiple meanings, such as land or possessions.
- The root word of Commutative Property is commute, which means to move around. Students may have heard others talk about how long it takes them to commute from home to work, or move around from home to work. Help students connect the Commutative Property to the idea that they're moving around, or changing the order of the numbers being added or multiplied.
- The root word of Associative Property is associate, which means to put things together. For example, students may associate dogs with barking. In mathematics we often use parentheses to put things together. Help students connect the Associative Property to the idea that they're using parentheses to put together groups of numbers that are being added or multiplied;
- The root word of Distributive Property is distribute, which means to spread about among several. Help students connect the Distributive Property of Multiplication over Addition or Subtraction to the idea that you're spreading out the multiplying over the quantities being added or subtracted;
- Use graphic organizers such as the Frayer model shown below, for vocabulary development.
In this unit, students create a shape sorter and consider all possibilities that will return its shape to its original position. To learn about the commutative and associate properties, they investigate the results when two of these moves are performed consecutively.
This website uses a game format for students to practice fluency and estimation skills for mental calculations involving whole numbers.
This website uses a game format for students to practice fluency for mental calculations involving negative integers.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) Teachers are: (descriptive list) using the commutative, associative, and distributive properties for mental math calculations with whole numbers asking students to explain their thinking when calculating mentally with whole numbers, and helping them see how the properties are being used using concrete and pictorial representations to model algebraic expressions scaffolding learning to move students from concrete and semi-concrete to abstract representations of algebraic expressions applying the order of operations and properties to generate equivalent numeric and algebraic expressions connecting students' experiences with order of operations and properties involving numeric expressions to experiences with algebraic expressions evaluating algebraic expressions by replacing variables with positive rational numbers using algebraic expressions from real-life, such as $\pi {r}^{2}$ and lwh, as a source of rich problems for students to evaluate using positive rational numbers using mathematical language in verbal and written communication requiring students to explain their reasoning and justify their solutions solving problems involving positive rational numbers by applying the order of operations and commutative, associative, and distributive properties posing questions that require students to apply the order of operations and various properties in order to solve
Parent Resources
● Commutative, Associative, and Distributive Laws
This website provides an explanation of the properties, and includes practice questions and an activity.
This website is an interactive game where students practice order of operations and fluency with whole number facts.
This website provides students with practice identifying four properties that involve addition: commutative, associative, additive identity, and distributive.
● Properties of Multiplication
This website provides students with practice identifying four properties that involve addition: commutative, associative, multiplicative identity, and distributive.
● Order of Operations I
This website uses a game format for students to practice fluency and estimation skills for mental calculations involving whole numbers.
