1.3.1 Shapes
Describe the characteristics of basic shapes. Use basic shapes to compose and decompose other objects in various contexts.
Describe characteristics of two- and three-dimensional objects, such as triangles, squares, rectangles, circles, rectangular prisms, cylinders, cones and spheres.
For example: Triangles have three sides and cubes have eight vertices (corners).
Compose (combine) and decompose (take apart) two- and three-dimensional figures such as triangles, squares, rectangles, circles, rectangular prisms and cylinders.
For example: Decompose a regular hexagon into 6 equilateral triangles; build prisms by stacking layers of cubes; compose an ice cream cone by combining a cone and half of a sphere.
Another example: Use a drawing program to find shapes that can be made with a rectangle and a triangle.
Overview
Standard 1.3.1 Essential Understandings
First grade students describe the characteristics of two- and three-dimensional shapes including triangles, squares, rectangles, circles, rectangular prisms and cylinders. These characteristics include the number of sides and vertices (corners). They put shapes together and take shapes apart in order to make new shapes.
All Standard Benchmarks - with codes
1.3.1.1 Describe characteristics of two- and three-dimensional objects, such as triangles, squares, rectangles, circles, rectangular prisms, cylinders, cones and spheres.
1.3.1.2 Compose (combine) and decompose (take apart) two- and three-dimensional figures such as triangles, squares, rectangles, circles, rectangular prisms and cylinders.
Benchmark Group A
1.3.1.1 Describe characteristics of two- and three-dimensional objects, such as triangles, squares, rectangles, circles, rectangular prisms, cylinders, cones and spheres.
1.3.1.2 Compose (combine) and decompose (take apart) two- and three-dimensional figures such as triangles, squares, rectangles, circles, rectangular prisms and cylinder
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Describe attributes of two-dimensional shapes (e.g., number of sides and corners).
- Describe the attributes of three-dimensional shapes.
- Identify two-dimensional shapes as faces of three-dimensional figures.
- Compose and decompose shapes using materials such as pattern blocks, geoblocks or tangram pieces.
Work from previous grades that supports this new learning includes:
- Recognizing basic two- and three-dimensional shapes such as squares, circles, triangles, rectangles, trapezoids, hexagons, cubes, cones, cylinders and spheres.
- Sorting objects using characteristics such as shape, size, color and thickness.
- Using basic shapes and spatial reasoning to model objects in the real-world.
NCTM Standards
Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships
PreK-2 Expectations
- recognize, name, build, draw, compare, and sort two- and three-dimensional shapes.
- describe attributes and parts of two- and three-dimensional shapes.
- investigate and predict the results of putting together and taking apart two- and three-dimensional shapes.
Common Core State Standards
Reason with shapes and their attributes.
1.G.1. Distinguish between defining attributes (e.g., triangles are closed and three-sided) versus non-defining attributes (e.g., color, orientation, overall size); build and draw shapes to possess defining attributes.
1.G.2. Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, half-circles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composite shape.
1.G.3. Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of. Describe the whole as two of, or four of the shares. Understand for these examples that decomposing into more equal shares creates smaller shares.
Misconceptions
Students may think . . .
- the shape changes as orientation changes.
- an equilateral triangle is the only kind of triangle.
Vignette
On the table in the front of the classroom is a set of geoblocks and other three-dimensional objects. The objects include a cereal box, a tissue box, book, soup can, building blocks and a set of geoblocks out on the table.

Mrs. VB picks up the large cube and distributes a smaller cube to each student.
Mrs. VB: What can you tell me about this shape?
Student: It's wood.
Student: It looks like a box; a really small box.
Student: It has points.
Mrs. VB: Can you show us?
Student indicates a "point."

Mrs. VB: Can you think of another word we could use instead of points?
Student: Corners.
Mrs. VB: Yes, this is a corner. Mathematicians use another word for corner. They call a corner a "vertex."
Mrs. VB writes on a chart.
corner -- vertex
Mrs. VB: Can you tell me what a mathematician calls a corner?
Students: Vertex
Mrs. VB.: Point to a corner on your cube.
Mrs. VB: If there is more than one corner we say corners. If there is more than one vertex mathematicians say vertices.
Mrs. VB. adds to the chart.
corner -- vertex
corners -- vertices more than one vertex
Mrs. VB. draws attention to the cube.
Mrs. VB: How can we count the vertices on my shape?
Students: Touch them and then count.
Mrs. VB: Count the vertices as I point.
Mrs. VB. begins by touching a corner and the students begin counting. Mrs. VB. knows she is going to touch each corner/vertex more than once as she continually turns the shape for all to see.
Students: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14...
Student: You are pointing to the corners over and over. We counted too many corners.
Most students agree.
Mrs. VB: How can we keep track of the vertices we count?
Student: We could mark them with a pencil like we do when we count pictures. It is easy to tell the ones we have counted when we mark them.
Mrs. VB: Unfortunately, we can't make any marks on the shapes with pencils or crayons.
Student: If you don't turn the shape we can count the corners at the top and then we can count the corners on the bottom.
Mrs. VB: Would you show us?
Student comes up, takes the cube and starts counting the vertices pointing to each one on the top and then counts each one on the bottom. Other students join the counting.
Mrs. VB.: Now count the vertices on your cube.
Mrs. VB: How many did you count?
Student: 8, 4 on the top and 4 on the bottom.
Mrs. VB: The shape has 8 vertices. We might say the shape has 8 corners.
Mrs. VB. holds up the cube.
Mrs. VB: What else can you tell me about this shape?
Student: It has sides.
Mrs. VB: Show us where you see sides.
Student indicates "side" on cube.

Mrs. VB: Can you think of another word that mathematicians would use instead of side?
Student: I remember! In Kindergarten my teacher told me a side was called a face. I thought that was funny because there are no eyes or nose or mouth!
Mrs. VB: That's right. Mathematicians call this a face. The word face has more than one meaning.
Mrs. VB adds to the chart.
corner -- vertex
corners -- vertices (more than one vertex)
side -- face
Mrs. VB: How many faces does a cube have?
Students count the faces on their cubes. Many students over counted as they kept turning the cube. Mrs. VB selects one student that she knows has counted correctly to demonstrate how he counted the faces.
Student: (Coming to the front and taking the cube, begins counting aloud.) 1, 2, 3, 4...stopping...thinking she is done. Oh, I forgot the top and bottom! 5, 6. Six in all!
Mrs VB: Good. Nice job correcting your thinking. What do you notice about the face?
Student: I know, I know, it's a square!
Mrs. VB: Do all the faces have the same shape? (turns the cube so students can see all faces.)
Students: Yes!
Student: Is this a special part? (points to edge.)

Student: Is it an end because it is the end of a side? Or I mean it is the end of a face?
Mrs. VB: You are right. It is at the end of this face and this face (pointing to two adjacent faces). Mathematicians call it an edge.
Mrs. VB adds to the chart.
corner -- vertex
corners -- vertices (more than one vertex)
side -- face
end -- edge
Mrs. VB: How many edges do you think a cube has? Talk to your partner about how you might count the edges.
Students immediately begin counting edges. They are unable to keep track of the edges as they are counting because they rotate the shape to see each face. This results in over or under counting.
At this point, Mrs. VB. realizes it would have been easier to have used a different rectangular prism as the basis for this lesson. A rectangular prism having different size faces might have made the counting of edges easier.
Mrs. VB.: How many edges did you count?
Students: 10, 16, 20, 8, 12 Mrs. VB. records these on the board.
Mrs. VB. has decided to stop the lesson at this point. Tomorrow the discussion of faces, vertices and edges will continue with a different rectangular prism. The students will come back to the task of counting of edges on a cube after they have worked with another rectangular prism.
Resources
Teacher Notes
- Students may need support in further development of previously studied concepts and skills.
- Geometric experiences (not developmental stages) are the greatest factor in advancing students geometric knowledge. Exploration allows children to talk about, explore and engage with content at the next level while increasing experiences at their current level. These explorations provide students with the best chance of advancing geometric thought.
- The van Hiele Levels of Geometric Thought, adapted from: Van de Walle, J. (2006), and Van de Walle, J., & Lovin, L. (2006).
The van Hiele Levels of Geometric Thought is a hierarchy describing the way that students learn to reason about shapes and other geometric ideas. There are five levels in the hierarchy that are deemed to be sequential. Students need to move through each prior level before moving on to the next. Student thinking about particular concepts will likely be at different levels at any given time. The levels describe how we think and what types of geometric ideas we think about, rather than how much knowledge we have. Movement through the levels depends on the types and amount of experiences students have with geometry. Instruction that takes place at a level higher than the students' functional level will be ineffective. Many adults remain at level 1 even though they have had a geometry course in high school. With appropriate experiences, however, students can reach level 2 in elementary school.
Level 0 - Visualization
The objects of thought at level 0 are shapes and what they "look like."
Students may be able to talk about the properties of the shapes, but the properties are not thought about explicitly. They characterize individual shapes based on appearance. "It is a square because it looks like a square." At this level, students think shapes "change" or have different properties when rotated or rearranged.
The products of thought at level 0 are classes or groupings of shapes that seem to be alike.
Level 1 - Analysis
The objects of thought at level 1 are classes of shapes rather than individual shapes.
Students are able to think of properties (number of sides, angles, parallel sides, etc.) of a shape rather than focusing on the appearance of a shape. A student operating at this level might list all the properties the student knows about a shape, but not discern which properties are necessary and which are sufficient to identify the shape. "It is a square because it has square corners and the sides are the same." Though students see properties of shapes, they cannot make generalizations about how different shapes relate to one another. Students at this level will not see the relationship of a square to a rectangle.
The products of thought at level 1 are the properties of shapes.
Level 2 - Informal Deduction or Abstraction
The objects of thought at level 2 are the properties of shapes.
Students develop relationships between and among properties. Shapes can be classified using minimal characteristics; e.g., "Rectangles are parallelograms with a right angle." Students at level 2 will be able to follow an informal deductive argument about shapes and their properties. While many adults remain at level 0 or level 1, with appropriate experiences, most students could reach level 2 by the end the elementary grades.
The products of thought at level 2 are relationships among properties of geometric objects.
Level 3 - Deduction
The objects of thought at level 3 are relationships among properties of geometric objects.
Students work with abstract statements about geometric properties and make conclusions based on logic. This is the level of a traditional high school geometry course.
The products of thought at level 3 are deductive axiomatic systems for geometry.
Level 4 - Rigor
The objects of thought at level 4 are deductive axiomatic systems for geometry.
Students operating at this level focus on axiomatic systems, not just deductions within the system. This is usually at a level of a college geometry course.
The products of thought at level 4 are comparisons and contrasts among different axiomatic systems of geometry.
Note: In some literature the van Hiele Levels of Geometric Thought are labeled 1-5 rather than 0-4.
For further information on the van Hiele Levels of Geometric Thought see this page.
- Students draw two-dimensional shapes because they are flat. They build three-dimensional shapes because they have depth.
- Students should see a variety of triangles, rectangles, and hexagons. Triangles that are not equilateral or isosceles need to be included.
- Students should see both examples and non-examples of shapes. Non-examples help students eliminate unimportant features and focus on relevant ones.
- Dynamic Paper
Need a set of pattern blocks where all shapes have one-inch sides? You can create all these things and more with the Dynamic Paper tool. Place the images you want, then export it as a PDF or as a JPEG image for use in other applications. Source.
Questions
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no".
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if . . . ?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to ...?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work? Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part ...
(Adapted from They're Counting on Us, California Mathematics Council, 1995)
NCTM Illuminations
- I've seen that Shape Before
Students learn the names of solid geometric shapes and explore their properties. At various centers, they use physical models of simple solid shapes, including cubes, cones, spheres, rectangular prisms, and triangular prisms. Source.
Students compare and sort rectangles and special rectangles called squares learning to distinguish between the two using their attributes. They will use manipulatives to form squares and rectangles. They will also identify and take pictures of squares and rectangles around school and make a class book.
- Investigating Shapes (Triangles)
Recognizing and understanding the properties of triangles and their positions in space are foundational to young students' knowledge of geometry. In these lessons, students identify characteristics of triangles, manipulate electronic geoboards to construct triangles, and name the triangles' relative locations. In addition, through music and observation, students identify triangles in their environment. These lessons are especially appropriate for students in prekindergarten and kindergarten.
These lessons comprise a series of learning experiences. For students to fully understand the concepts presented here, it is recommended that these lessons be included in a more fully developed Standards-based unit on geometry rather than used as stand-alone lessons.
Additional Instructional Activities
- Visualization
Drawing and sketching shapes is an important part of developing spatial sense. A shape is displayed on an overhead projector for two to three seconds. Students draw the shape when the projector is turned off. Drawing while the projector is off requires students to remember details about the shape they saw. The original figure is again briefly displayed, and children make a second attempt at drawing it. Giving the students a chance to explain what they saw and how they drew the shape is important. Note: If students draw the shape as they see it the first time they are copying the shape not visualizing the shape. The intent of this activity is to give students a chance to develop mental images.

- Paper Folding
Children can fold and then cut paper shapes to make new shapes.
- Yarn Shapes
Using a piece of yarn, students can form simple two-dimensional shapes. Several children can work to form a shape using a longer piece of yarn.
Findell, C., Small, M., Cavanagh, M., Dacey, L., Greenes, C., & Scheffield, L. (2001). Navigating through geometry in prekindergarten-grade 2. Reston, VA: National Council of Teachers of Mathematics.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Richardson, K. (1999). Understanding geometry. Bellingham, WA: Lummi Bay Publishing.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J., & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
New Vocabulary
"Vocabulary literally is the key tool for thinking."
Ruby Payne
rectangular prisms: the base of the prism is a rectangle
right cylinder: cylinders with bases aligned one directly above the other
vertex: point where the surfaces meet--corner
face: flat surface of the three-dimensional shape
edge: where two surfaces join (intersect)
Mathematics vocabulary words describe mathematical relationships and concepts and cannot be understood by simply practicing definitions. Students need to have experiences communicating ideas using these words to explain, support, and justify their thinking.
Learning vocabulary in the mathematics classroom is contingent upon the following:
Integration: Connecting new vocabulary to prior knowledge and previously learned vocabulary. The brain seeks connections and ways to make meaning which occurs when accessing prior knowledge.
Repetition: Using the word or concept many times during the learning process and connecting the word or concept with its meaning. The role of the teacher is to provide experiences that will guarantee connections are made between mathematical concepts, relationships, and corresponding vocabulary words.
Meaningful Multiple and varied opportunities to use the words in context. These
Use: opportunities occur when students explain their thinking, ask clarifying questions, write about mathematics, and think aloud when solving problems. Teachers should be constantly probing student thinking in order to determine if students are connecting mathematics concepts and relationships with appropriate mathematics vocabulary.
Strategies for vocabulary development
Students do not learn vocabulary words by memorizing and practicing definitions. The following strategies keep vocabulary visible and accessible during instruction.
Mathematics Word Bank: Each unit of study should have word banks visible during instruction. Words and corresponding definitions are added to the word bank as the need arises. Students refer to word banks when communicating mathematical ideas which leads to greater understanding and application of words in context.
Labeled pictures and charts: Diagrams that are labeled provide opportunities for students to anchor their thinking as they develop conceptual understanding and increase opportunities for student learning.
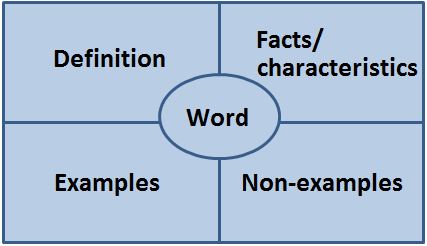
Frayer Model: The Frayer Model connects words, definitions, examples and non-examples.
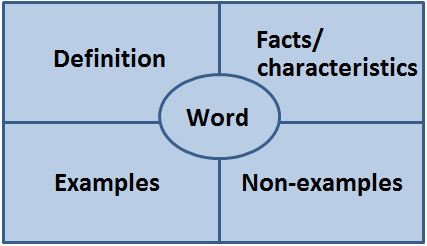
Example/Non-example Charts: This graphic organizer allows students to reason about mathematical relationships as they develop conceptual understanding of mathematics vocabulary words. Teachers should use these during the instructional process to engage student in thinking about the meaning of words.

Vocabulary Strips: Vocabulary strips give students a way to organize critical information about mathematics vocabulary words.
|
word |
definition |
illustration |
Encouraging students to verbalize thinking by drawing, talking, and writing increases opportunities to use the mathematics vocabulary words in context.
Additional Resources for Vocabulary Development
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks:
What are the key ideas related to describing characteristics of basic two- and three-dimensional objects at the first grade level? How do student misconceptions interfere with mastery of these ideas?
What experiences do students need in order to describe characteristics of two- and three-dimensional shapes successfully?
Examine student work related to a task describing characteristics of two- and three-dimensional shapes. What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
What are the key ideas related to composing and decomposing two- and three-dimensional figures at the first grade level? How do student misconceptions interfere with mastery of these ideas?
What experiences do students need in order to compose and decompose two- and three-dimensional figures successfully?
Examine student work related to a task involving composing and decomposing two- and three-dimensional figures. What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
How can teachers assess student learning related to these benchmarks?
How are these benchmarks related to other benchmarks at the first grade level?
Professional Learning Community Resources
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K.. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Chapin, S. and Johnson, A. (2006). Math matters, understanding the math you teach, grades K-8. (2nd ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Fuson, K., Clements, D., & Beckmann, S. (2009). Focus in grade1: Teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, Arthur. (2006). Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Sammons, L. (2011). Building mathematical comprehension using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Bender, W. (2009). Differentiating math instruction-Strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Burns, M. (Ed.). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Chapin, S. and Johnson, A. (2006). Math matters, understanding the math you teach, grades k-8. (2nd ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Dacey, L., & Salemi, R. (2007). Math for all: Differentiating instruction k-2. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Fuson, K., Clements, D., & Beckmann, S. (2009). Focus in grade1: Teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, A. (2006). Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom-A guide for teachers k-8. Portsmouth, NH: Heinemann.
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Richardson, K. (1999). Understanding geometry. Bellingham, WA: Lummi Bay Publishing.
Sammons, L. (2011). Building mathematical comprehension-Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J., Charles, R., Clements, D., Duckett, P., Fennell, F., ..., & Zbiek, R. M. (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: A quest for coherence. Reston, VA: NCTM.
Seeley, C. (2009). Faster isn't smarter-Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., & Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
Assessment
- Use pattern blocks to fill this shape. Raise your hand to show your teacher when you are done.
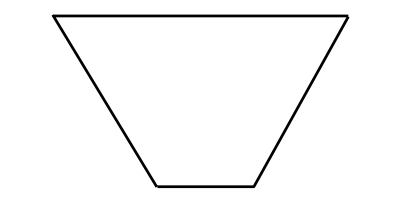
Solution: Student correctly fills the space with blocks.
Benchmark: 1.3.1.2
- Use pattern blocks to fill this shape. Raise your hand to show your teacher when you are done.
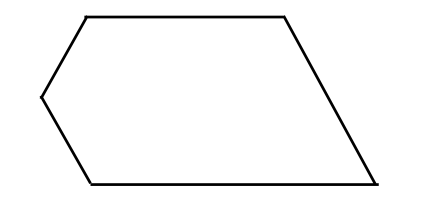
Solution: Student correctly fills the space with blocks.
Benchmark: 1.3.1.2
- Use pattern blocks to fill this shape. Raise your hand to show your teacher when you are done.
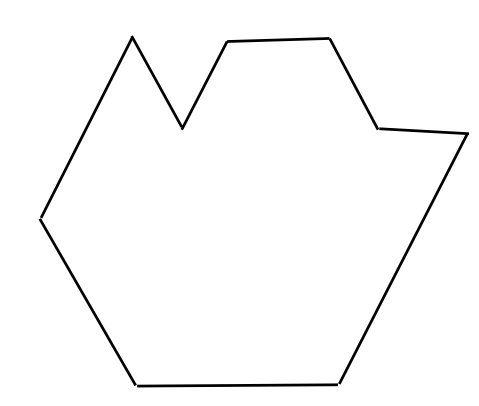
Solution: Student correctly fills the space with blocks.
Benchmark: 1.3.1.2
- Use a yellow crayon to circle the cones.
Use a red crayon to circle the cylinders.
Use a blue crayon to circle the rectangular prism. 
Solution: Student uses the correct color to circle the correct shape.
Benchmark: 1.3.1.1
- Given a rectangular prism,
1. Count the faces. How many faces are there?
2. Count the vertices. How many vertices are there?
3. Count the edges. How many edges are there?
Solution: 1. Six
2. Eight
3. Twelve
Benchmark: 1.3.1.1
Differentiation
Students need tactile experiences with two- and three-dimensional shapes as they learn to identify, match and then describe these shapes. Being able to move shapes as they try to match shapes is critical as they recognize the attributes so they can compare and classify shapes.
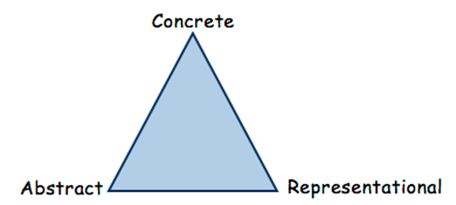
Concrete - Representational - Abstract Instructional Approach
The Concrete-Representational-Abstract Instructional Approach (CRA) is a research-based instructional strategy that has proven effective in enhancing the mathematics performance of students who struggle with mathematics.
The CRA approach is based on three stages during the learning process:
Concrete - Representational - Abstract
The Concrete Stage is the doing stage. The concrete stage is the most critical in terms of developing conceptual understanding of mathematical skills and concepts. At this stage, teachers use manipulatives to model mathematical concepts. The physical act of touching and moving manipulatives enables students to experience the mathematical concept at a concrete level. Research shows that students who use concrete materials develop more precise and comprehensive mental representations, understand and apply mathematical concepts, and are more motivated and on-task. Manipulatives must be selected based upon connections to the mathematical concept and the students' developmental level.
The Representational Stage is the drawing stage. Mathematical concepts are represented using pictures or drawings of the manipulatives previously used at the Concrete Stage. Students move to this level after they have successfully used concrete materials to demonstrate conceptual understanding and solve problems. They are moving from a concrete level of understanding toward an abstract level of understanding when drawing or using pictures to represent their thinking. Students continue exploring the mathematical concept at this level while teachers are asking questions to elicit student thinking and understanding.
The Abstract Stage is the symbolic stage. Teachers model mathematical concepts using numbers and mathematical symbols. Operation symbols are used to represent addition, subtraction, multiplication and division. Some students may not make a clean transfer to this level. They will work with some symbols and some pictures as they build abstract understanding. Moving to the abstract level too quickly causes many student errors. Practice at the abstract level will not lead to increased understanding unless students have a foundation based upon concrete and pictorial representations.
Additional Resources
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades k-2. Sausalito, CA: Math Solutions.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
- Connecting vocabulary to the attributes of a shape can be challenging. English Language Learners need opportunities to use these words repeatedly. Labeled representations of shapes help students solidify their understanding of the language.
- Word banks need to be part of the student learning environment in every mathematics unit of study.
- Use vocabulary graphic organizers such as the Frayer model (see below) to emphasize vocabulary words count, first, second, third, etc.
- Sentence Frames
Math sentence frames provide support that English Language Learners need in order to fully participate in math discussions. Sentence frames provide appropriate sentence structure models, increase the likelihood of responses using content vocabulary, help students to conceptualize words and build confidence in English Language Learners.
Sample sentence frames related to these benchmarks:
|
This is a _____________ because it has ________________. |
|
_________________ have ______ number of sides. |
|
______________ is not a _______________ because ______________. |
|
I can make a ___________ using ________________. (square, 2 triangles) |
- When assessing the math skills of an ELL student it is important to determine if the student has difficulty with the math concept or with the language used to describe the concept and conceptual understanding.
Additional ELL Resources
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
- Using 3-D shapes in individual paper bags, students put their hand inside the bag to touch the shape. They describe the shape, identify the shape and check the identity of the shape by removing the shape from the bag.
Additional Resources
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades k-2.Sausalito, CA: Math Solutions.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Parents/Admin
|
Students are ... |
Teachers are ... |
|
using mathematical language to describe shapes. |
asking open-ended questions about objects; e.g., What can you tell me about this shape? |
|
creating shapes by drawing, making models (straws, geoboards, clay), and using technology. |
providing opportunities for students to explore, to see and feel, to build and take apart, and to make observations. |
|
describing characteristics of two- and three-dimensional shapes (triangles, squares, cylinders etc). |
asking questions, "What similarities do you notice with these shapes? Do you think all squares will have those characteristics?" Questioning students will help them write conjectures about shapes. |
|
using pattern blocks and other materials to compose and decompose shapes. |
asking, "What shapes can you use to make a square? Rectangle? How will you know if it is a square? What shapes did you make when you folded the paper in half?" |
Additional Resources
For Mathematics Coaches
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach: Grades k-8, 2nd edition. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
For Administrators
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for school administrators. Reston, VA: National Council of Teachers of Mathematics.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Mathematics handbooks to be used as home references:
Cavanagh, M. (2004). Math to Know: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Helping your child learn mathematics
Provides activities for children in preschool through grade 5
What should I look for in the mathematics program in my child's school? A Guide for Parents developed by SciMathMN
Help Your Children Make Sense of Math
Ask the right questions
In helping children learn, one goal is to assist children in becoming critical and independent thinkers. You can help by asking questions that guide, without telling them what to do.
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if . . . ?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to ...?
Can you make a prediction?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work?
Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part...
Adapted from They're counting on us, California Mathematics Council, 1995
