7.1.1B Representing & Comparing Rational Numbers
Locate positive and negative rational numbers on a number line, understand the concept of opposites, and plot pairs of positive and negative rational numbers on a coordinate grid.
Compare positive and negative rational numbers expressed in various forms using the symbols < , > , = , ≤ , ≥ .
For example: -$\frac{1}{2}$< -0.36
Recognize and generate equivalent representations of positive and negative rational numbers, including equivalent fractions.
For example: $-\frac{40}{12}=-\frac{120}{36}=-\frac{10}{3}=-3.\bar{3}$.
Overview
Standard 7.1.1 Essential Understandings
Students have had prior experience with reading, writing and representing positive rational numbers as fractions, decimals, percents and ratios. They are fluent in writing positive integers as products of factors. They have developed a sense for the relative size of integers and can compare and order positive rational numbers. Students have been using positive rational numbers in a variety of ways: to label, measure, locate, compare and quantify. They are able to plot these values on a number line and also on a coordinate grid. Students will extend their understandings to all rational numbers, including negative values. Progression from just representation of value to comparison of values, both in the positive and now the negative, is strengthened in this standard. This standard extends the representation of equivalent representations of positive rational numbers to negative values. Students have also had prior experience plotting points in quadrant 1 on the coordinate grid. This standard extends the coordinate plane to all four quadrants.
In addition, students will deepen their understanding of the definition and meaning of a rational number. Students who master identifying examples of rational numbers in 7th grade will be prepared for the introduction to irrational numbers in 8th grade.
All Standard Benchmarks
7.1.1.1 Know that every rational number can be written as the ratio of two integers or as a terminating or repeating decimal. Recognize that π is not rational, but that it can be approximated by rational numbers such as 22/7 and 3.14.
7.1.1.2 Understand that division of two integers will always result in a rational number. Use this information to interpret the decimal result of a division problem when using a calculator.
7.1.1.3 Locate positive and negative rational numbers on the number line, understand the concept of opposites, and plot pairs of positive and negative rational numbers on a coordinate grid.
7.1.1.4 Compare positive and negative rational numbers expressed in various forms using the symbols <, >, ≤, ≥.
7.1.1.5 Recognize and generate equivalent representations of positive and negative rational numbers, including equivalent fractions.
Benchmark Group B - Representing and Comparing Rational Numbers
7.1.1 Fraction & Decimals: Representations and Relationships
7.1.1.3 Locate positive and negative rational numbers on the number line, understand the concept of opposites, and plot pairs of positive and negative rational numbers on a coordinate grid.
7.1.1.4 Compare positive and negative rational numbers expressed in various forms using the symbols <, >, ≤, ≥.
7.1.1.5 Recognize and generate equivalent representations of positive and negative rational numbers, including equivalent fractions.
What students should know and be able to do [at a mastery level] ] related to these benchmarks
- Locate any rational number on a number line as well as compare and order positive and negative numbers with or without the use of a number line;
- Plot coordinate points in all four quadrants of the coordinate grid;
- Translate all rational numbers, both positive and negative, between decimal and fractional form as well as equivalent fractional representations;
- Compare all positive rational numbers using <, >, ≤, ≥ and =;
- Order positive and negative numbers in any form;
- Generate equivalent fractions and go between them fluently;
- Generate equivalent decimal representations for fractional values and vice versa;
- Order fractions, decimals and integers, including positive and negative values.
Work from previous grades that supports this new learning includes:
- Understand equivalence of, and translations between, positive rational numbers in fraction and decimal form;
- Have experience with the fraction bar symbol for division;
- Use a number line to locate, order, and compare positive rational numbers;
- Be able to use <, =, and > symbols;
- Be able to use the first quadrant of the coordinate grid as well as have experience with using the x-coordinate and y-coordinate relationship;
- Locate positive rational numbers on a number line and plot pairs of positive rationals on a coordinate grid
- Understand and apply arithmetic operations with positive rational numbers;
- Use a number line to develop equivalence and operations of positive fractions and decimals.
NCTM Standards
Understand numbers, ways of representing numbers, relationships among numbers, and number systems.
- Compare and order fractions, decimals, and percents efficiently and find their approximate locations on a number line;
- Develop meaning for integers and represent and compare quantities with them.
Common Core State Standards (CCSS)
6.NS (The Number System) Apply and extend previous understandings of numbers to the system of rational numbers.
- 6.NS.5. Understand that positive and negative numbers are used together to describe quantities having opposite directions or values (e.g., temperature above/below zero, elevation above/below sea level, credits/debits, positive/negative electric charge); use positive and negative numbers to represent quantities in real-world contexts, explaining the meaning of 0 in each situation.
- 6.NS.6. Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
6.NS.6.a. Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., -(-3) = 3, and that 0 is its own opposite.
6.NS.6.b. Understand signs of numbers in ordered pairs as indicating locations in quadrants of the coordinate plane; recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
6.NS.6.c. Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
- 6.NS.7. Understand ordering and absolute value of rational numbers.
6.NS.7.a. Interpret statements of inequality as statements about the relative position of two numbers on a number line diagram. For example, interpret -3 > -7 as a statement that -3 is located to the right of -7 on a number line oriented from left to right.
6.NS.7.b. Write, interpret, and explain statements of order for rational numbers in real-world contexts. For example, write -3 degrees C > -7 degrees C to express the fact that -3 degrees C is warmer than -7 degrees C.
7NS (The Number System) Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers.
- 7 NS.2. Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
7.NS.2.d. Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats
8NS (The Number System) Know that there are numbers that are not rational, and approximate them by rational numbers.
- 8.NS.1. Know that numbers are not rational are called irrational. Understand informally that every number has a decimal expansion; rational numbers have decimal expansions that terminate in 0s or eventually repeat, and conversely.
Misconceptions
Student Misconceptions and Common Errors
- When comparing fractions, students may focus only on the size of the denominator. For example, students may mistakenly think $ \frac{4}{9}$ is larger than $ \frac{4}{5}$ because 9 is larger than 5.
- Students sometimes confuse the <, >, ≤, and ≥ symbols.
- Students might think that all improper fractions need to be written as mixed numbers. For example, they might think that 3.3 is the same as 10/3 and that they must use the repeating bar or use ⅓.
- Students think a larger digit always is the larger number, but with negatives that is not the case; the farther to the left it is, the smaller it is. For example, -6 > -9 because -6 is closer to zero on the left side, therefore it is greater.
- Students misnumber the quadrants, starting in the upper right and going clockwise.
- Students sometimes are not aware what ≤ and ≥ are. They sometimes think that 5 ≤ 10 is not true because 5 is not equal to 10.
- Students sometimes have trouble when plotting points that are on an axis. For example, for (0, 4) or (-2, 0), they realize the points should be on an axis but they sometimes place it on the wrong axis.
Vignette
In the Classroom
This vignette describes a notecard order activity, in which the students choose notecards, each marked with a different number. The students are then asked to put themselves in order based on their numbers. When the teacher prepares cards for the students, different types of numbers are used, including integers, fractions, decimals, negative values, etc.
Teacher: OK, class, I need each of you to pick a notecard. On it you will find a number, maybe an integer, maybe a decimal, maybe a fraction. It could also be positive or negative. Your task is to get yourselves in order in the room - the front of the room is the largest value, and the back of the room is the lowest value. You need to do this task without talking. Good luck.
As the teacher walks around the room, she notices right away that the positive values are all gathered at the front of the room. After about a minute, she stops the group.
Teacher: OK, we're starting to get organized. Let's try to figure out the order we need to be in. Think of equivalences among your values, or benchmarks your value is close to. You may now talk to your classmates, but you cannot tell anyone else where their values go, but you can help them figure out equivalent values in another form. For example, if my value was 0.5, what is an equivalent fraction?
Student: 1/2?
Teacher: Yes. Exactly. Now continue working together to get yourselves in the correct order. When you think you are in the right order, check with both people on either side of you. When you think the entire class is correct, let me know.
The students continue to work to get in order. One student is really struggling with the value of -1/3, because he sees another person with -0.3 and can't decide on which side of that person he needs to be standing.
Teacher: OK, Mike, what part of your value of -1/3 are you stuck with, the negative part or the fractional part?
Student: Both, actually. I know I need to be on the side of 0 that is closer to the back of the room, but I'm confused on which side I am of -0.3. I don't know if I'm bigger or smaller that it.
Teacher: You are right that you need to be closer to the back of the room. OK, how about this: Do you know a fractional equivalence to 0.3?
Student: Um, I think it is 30%. But I do not know what fraction that is.
Teacher: Well, we know that percent means "out of 100," so we could rewrite 30% as 30/100. Right?
Student: Yes. I guess we can.
Teacher: OK. Let's simplify that. It is the same as...
Student: 3/10?
Teacher: Yes. We're getting closer to what we need. Now we need to compare ⅓ to 3/10. How about if we graph those two values, looking at the numerator as the x-coordinate and the denominator as the y-coordinate. So if we look at those graphs, what do you see?
Student: That the line of ⅓ is steeper than the line of 3/10.
Teacher: So what does that mean?
Student: That ⅓ is greater than 3/10.
Teacher: Right. Now, if we are on the negative side of 0, then where do you need to be? Closer to zero are farther from zero?
Student: Well, if ⅓ is greater than 3/10, then that means that -1/3 has a greater distance from 0 than 3/10, so I guess I need to be on the left of 3/10?
Teacher: What do you mean by left?
Student: Well, closer to the back of the room.
Teacher: Yes, you are correct.
The teacher looks at the rest of the class, and determines that they have indeed put themselves in the right order.
Also reference the following link for a vignette on the coordinate grid:
http://www.shodor.org/interactivate/discussions/IntroductionToTheCoo/
Resources
Teacher Notes
- A quick review of comparing/ordering/plotting of all forms of positive rational numbers might be beneficial before starting to include negative rational numbers into the mix for the first time.
- Help students understand that the smaller the number, the closer the number is to zero; therefore; if it is a negative number, it is actually greater than a negative number that is farther from zero.
- The understanding that -27 is less than -12 requires building mental images and physical/representational models that allow students to visualize these new comparisons and relationships.
- If numbers are negative, the one with the higher absolute value is smaller because it is farther away from zero in the negative direction.
- Have students work on graphing in all four quadrants and the numbering of them, starting in the upper right (where both x and y values are positive) and moving in counterclockwise form (I, II, III, IV).
- Students need help to remember which inequality is which. You can offer tips, such as alligator mouths ("the alligator eats the bigger number"), or < looks more like an L so it is less than. This website offers tips on this topic.
- Be deliberate in the teaching of ≤ and ≥ . Students need to realize that these are less than or equal to, so it could be either. The expression a ≤ b means that either a<b or a=b. Enforce the difference between < and >.
- Seventh grade is the first year when students work with negative rational numbers. Give students plenty of practice with plotting negative numbers (all representations) on a number line, comparing negative numbers and plotting ordered pairs that include negative coordinates.
Line 'Em Up
This website provides a self discovery approach to understand the process of plotting points on a coordinate plane, using a program for a TI graphing calculator.
Finding Your Way Around
Students explore two-dimensional space via an activity in which they navigate the coordinate plane. This NCTM Publication-Based Lesson Plan is adapted from the article: Schloemer, C.G. (September 1994). Tips for Teaching Cartesian Graphing: Linking Concepts and Procedures. InTeaching Children Mathematics, 1(1), 20-23.
Understanding Rational Numbers and Proportions
In this lesson, students use real-world models to develop an understanding of fractions, decimals, unit rates, proportions and problem solving. The three activities in this investigation center on situations involving rational numbers and proportions that students encounter at a bakery. These activities involve several important concepts of rational numbers and proportions, including partitioning a unit into equal parts, the quotient interpretation of fractions, the area model of fractions, determining fractional parts of a unit not cut into equal-sized pieces, equivalence, unit prices and multiplication of fractions.
Fraction game
This applet allows students to individually practice working with relationships among fractions and ways of combining fractions.
Additional Instructional Resources
To give students practice at using symbols in mathematical expressions, use index cards marked with rational numbers greater than or equal to zero. Students will draw two or more cards at random and compare numbers using =, < and >. \
Source: 2007 Mississippi Mathematics Framework Revised Strategies, p. 32.
Graph Mole game
This website offers an algebra game that teaches how to plot points on a Cartesian coordinate plane.
Plotting points and reading coordinates
This activity allows the user to plot points on the coordinate plane and to read the coordinates of a point plotted by the computer.
Guiding around the grid
On this website, students can guide Billy the Bug around the first quadrant of the coordinate grid to reach the given coordinate, and then "feed" him when he lands on the correct coordinate.
opposite: two numbers whose sum is 0. On a number line, opposites are the same distance from 0 but in different directions from 0. Opposites have the same absolute value. The number 0 is its own opposite.
Example: -3 and 3 are opposites.
origin: the point of intersection of the vertical and horizontal axes of a Cartesian plane. The coordinates of the origin are (0, 0).
x-coordinate: the first number of in ordered pair; the position of a point relative to the vertical axis.
y-coordinate: the second number in an ordered pair; the position of a point relative to the horizontal axis.
x-axis: the horizontal number line on the Cartesian coordinate plane.
y-axis: the vertical number line on the Cartesian coordinate plane.
quadrant: one of the four regions on a Coordinate plane formed by the intersection of the x-axis and the y-axis.
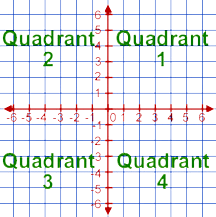
Points in Quadrant 1 have positive x and positive y coordinates.
Points in Quadrant 2 have negative x but positive y coordinates.
Points in Quadrant 3 have negative x and negative y coordinates.
Points in Quadrant 4 have positive x but negative y coordinates.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What do students already know about working with positive and negative numbers?
- What instructional strategies can be used to engage students with investigating relationships of equivalent positive or negative rational numbers?
- What different representations can be used to illustrate relationships of equivalent positive or negative rational numbers?
- What instructional strategies can be used to engage students with investigating comparing positive and/or negative rational numbers?
- What different representations can be used to illustrate comparing positive and/or negative rational numbers?
- What are the expected misconceptions students will have with comparing positive or negative rational numbers? What should be response be that will help them develop understanding?
- How do negative and positive numbers help in describing the situation?
- What will addition, subtraction, multiplication or division of positive and negative numbers tell about the problem?
- What model(s) for positive and negative numbers would help in showing the relationship in the problem situation?
- How can the instruction be scaffolded for students?
- Do the tasks that have been designed connect to underlying concepts or focus on memorization?
- How can it be determined whether students have reached this learning goal?
- How can be lesson be differentiated?
Materials
- Number line problem sets
- PowerPoint integer presentations This website has many integer PowerPoint presentations that are useful for teachers and good for parent reference.
- Ordered Simple Plot The ordered simple plotter allows the student to enter the coordinate pairs in the order of the drawing and it will plot the entered points thus revealing the accuracy of the coordinates and/or the interpretation of the recreator. Students are encouraged to use this tool to check their coordinates.
- Schielack, J., Charles, R., Clements, D., Duckett, P., Fennell, F.(Skip), Lewandowski, S., Trevino, E., and Zbiek, R.M. (2006). Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics: A Quest for Coherence. Reston, VA: National Council of Teachers of Mathematics.
- Linder-Scholer, W. (1998). SciMathMN: Minnesota K-12 Mathematics Frameworks. St. Paul, MN: SciMathMN.
- Lappan, G., Fey, J., Fitzgerald, W., Friel, S., and Philips, E. (2009). Accentuate the Negative, CMP2. Boston, Mass: Pearson.
- Introduction to negative numbers http://www.purplemath.com/modules/negative.htm
- Number types
Numbers are classified according to type. The first type of number is the first type you ever learned about: the counting, or "natural" numbers.
http://www.purplemath.com/modules/numtypes.htm
- Rational and irrational numbers http://www.themathpage.com/aPreCalc/rational-irrational-numbers.htm#rational1
- Coordinate plane and coordinates http://www.shodor.org/interactivate/discussions/IntroductionToTheCoo/
Assessment
Note: These exit slips can be used at the end of a class period as a quick assessment of student understanding of the material for the day. Give them to the students at the end of the period and collect them as they leave. Use the results to guide the next lesson.
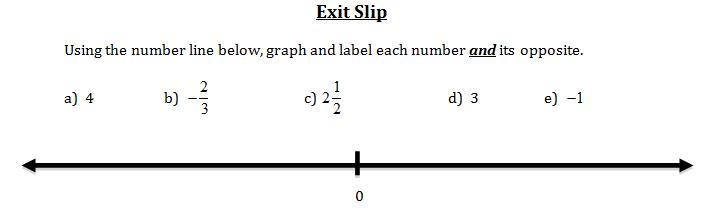
DOK Level: 2
Answer: Numbers in order should be: -4, -3, -$2\frac{1}{2}$, -1, -$\frac{2}{3}$, $\frac{2}{3}$, 1, $2\frac{1}{2}$, 3, 4.
Source: Minneapolis Public Schools Teacher created exit slip to assess benchmark 7.1.1.3
2.

DOK Level: 2
Answer: Numbers in order should be: -5, -3, -1, - ½ , 0, ½, 1, 3, 5.
Source: Minneapolis Public Schools Teacher created exit slip to assess benchmark 7.1.1.3
3. Which is equivalent to $5\frac{2}{15}$?
A. $5.1\overline{3}$
B. $5.\overline{1}$$\overline{3}$
C. 5.13
D. $5.\overline{3}$$$
DOK Level: 2
Answer: A
Source: Minnesota MCA Series III Mathematics' Item Sampler, Grade 7.
4.
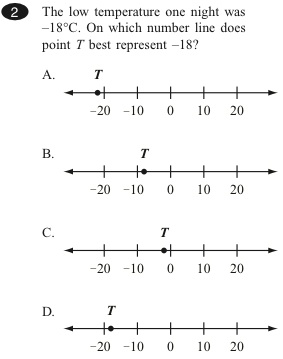
DOK Level: 2
Answer: D
Source: Massachusetts Comprehensive Assessment System Release of Spring 2009 Test Items
5.

DOK Level: 2
Answer: A
Source: Massachusetts Comprehensive Assessment System Release of Spring 2010 Test Items
6. Which lists the numbers in order from least to greatest?
A. 0.6, $\frac{7}{10}$, $\frac{2}{3}$, 64%
B. 0.6, 64%, $\frac{2}{3}$, $\frac{7}{10}$
C. $\frac{7}{10}$, $\frac{2}{3}$, 64%, 0.6
D. $\frac{2}{3}$, 64%, $\frac{7}{10}$, 0.6
DOK Level: 2
Answer: B
Source: Minnesota MCA Series III Mathematics' Item Sampler, Grade 7
7. True or False: A rational number is an integer.
DOK Level: 1
Answer: False. Some rational numbers are integers, but fractions are rational numbers but not integers.
Adapted from http://www.purplemath.com/modules/numtypes.htm
8. True or False: A number is either a rational or an irrational, but not both.
DOK Level: 1
Answer: True. In decimal form, a number is either non-terminating and non-repeating (so it's an irrational) or not (so it's a rational); there is no overlap between these two number types.
Adapted from: http://www.purplemath.com/modules/numtypes.htm
9. Use the graph below to identify the coordinates of the following points:
A _____________, D (_______________) G( __________________)
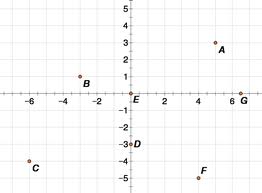
DOK Level: 1
Answers: A (5, 3); D (0, -3); G (6.5, 0)
10. Using the graph above, which point has the coordinates (-3, 1)?
A. Point A
B. Point B
C. Point D
D. Point F
DOK Level: 1
Answer: B
11. In which quadrant would the point (-3, 8) be?
A. Quadrant I
B. Quadrant II
C. Quadrant III
D. Quadrant IV
DOK Level: 1
Answer: B
Differentiation
- Students need to write all steps used in solving the problems. By writing their steps, it will help them remember what they are doing and guide them in the next problem.
- Encourage the use of the number line to make comparisons. Remind students that values increase as you move to the right. Include decimal and percent equivalency benchmark markings. For example, 1, 100% 0.5, ½, 50%.
- When struggling learners are comparing numbers, start by having them compare numbers that are of the same representation, such as all decimal numbers, until they have achieved mastery of each representation. Then introduce the task of comparing positive and negative rational numbers with mixed representation.
- Introduction to negative numbers This website has an introduction to negative numbers, including number line representation, comparing and then links to operations with positive and negative numbers. Reference this site with struggling learners to help them make the connection between negative numbers and what they already know about numbers.
- Students may confuse the math and non-math definitions of "opposite." Review examples of the non-math definition, such as "The two boys lived on opposite sides of the street," "the opposite bank of the river," or "fold the bottom right corner of the paper over to the opposite corner."
- Basic video on the quadrants and how they are numbered
- Graphing a coordinate and identifying its quadrant
- Use exponents within the numerical values, including negative exponents.
- Have students compare different sets of numbers that include rational and irrational values.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: (descriptive list) |
Teachers are: (descriptive list) |
|
using number lines (both vertically and horizontally) to locate, order and compare positive and negative rational numbers. |
engaging students with concrete and semi-concrete representations of rational numbers to develop student thinking. |
|
putting rational numbers (both positive and negative) in order from least to greatest, given a set of numbers. |
using real world terms to help students with ordering (money amounts, temperature, gains and losses in football), such as "How do you show that temperatures are below zero?" or "On a horizontal number line, where are the positive and negative numbers in relation to zero?" |
|
correctly using greater than/less than symbols in a numerical expressions. |
correcting students' miscalculations and placement of numbers by referencing the positive opposite of negative numbers. |
|
using number lines - both a single horizontal x axis as well as the x and y coordinate grid - to locate and compare positive and negative rational numbers. |
requiring students to match equivalent representations of positive and negative rational numbers. |
|
explaining how they are determining their solutions to the problems. |
asking students to compare all forms of rational numbers and representing those comparisons on a number line or with inequality symbols. |
|
understanding the concept of opposite with rational numbers by plotting a number and its opposite on a number line. |
having students plot coordinate pairs in all quadrants on the coordinate grid. |
|
|
suggesting students put rational numbers in the same "form" before comparing and ordering them. |
|
|
allowing students extensive practice with comparing negative rational numbers. |
Parent Resources:
- Ordering/comparing numbers
- Opposites
- Identify rational numbers
- Circle 0 activity
- General Coordinates Game
This activity allows the user to plot points on the coordinate plane and to read the coordinates of a point plotted by the computer.
This website has many integer PowerPoint presentations that are useful for teachers and good for parent reference.
