6.1.3C Problem Solving & Estimation
Solve real-world and mathematical problems requiring arithmetic with decimals, fractions and mixed numbers.
Estimate solutions to problems with whole numbers, fractions and decimals and use the estimates to assess the reasonableness of results in the context of the problem.
For example: The sum $\frac{1}{3}$+0.25 can be estimated to be between $\frac{1}{2}$ and 1, and this estimate can be used to check the result of a more detailed calculation.
Overview
Standard 6.1.3 Essential Understandings
Students at this level model multiplication and division of fractions and connect these models to procedures for multiplying and dividing fractions. Place-value patterns are used to multiply and divide finite decimals by powers of 10. The relationship between decimals and fractions, as well as the relationship between finite decimals (i.e., a finite decimal multiplied by an appropriate power of 10 is a whole number), is used to understand and explain the procedures for multiplying and dividing decimals. Common procedures are used to multiply and divide fractions and decimals efficiently and accurately. Problem solving with positive rational numbers is extended to include arithmetic with decimals, fractions, and mixed numbers. Students build on understanding that percents are ratios per 100 to solve problems in various contexts that require finding percent of a number or what percent one number is of another.
All Standard Benchmarks
6.1.3.1 Multiply and divide decimals and fractions using efficient and generalizable procedures, including standard algorithms.
6.1.3.2 Use the meanings of fractions, multiplication, division and the inverse relationship between multiplication and division to make sense of procedures for multiplying and dividing fractions.
6.1.3.3 Calculate the percent of a number and determine what percent one number is of another number to solve problems in various contexts.
6.1.3.4 Solve real-world and mathematical problems requiring arithmetic with decimals, fractions and mixed numbers.
6.1.3.5 Estimate solutions to problems with whole numbers, fractions and decimals and use the estimates to assess the reasonableness of results in the context of the problem.
Benchmark Group C
6.1.3.4 Solve real-world and mathematical problems requiring arithmetic with decimals, fractions and mixed numbers.
6.1.3.5 Estimate solutions to problems with whole numbers, fractions and decimals and use the estimates to assess the reasonableness of results in the context of the problem.
What students should know and be able to do [at a mastery level] related to these benchmarks
- Students will be able to choose the correct operation to solve real-world problems involving arithmetic of decimals, fractions, and mixed numbers;
- Students will be able to solve real-world and mathematical problems involving computation of positive rational numbers;
- Students will be able to convert among fractions, decimals, and percents, and decide which form to use in a given situation;
- Students will be able to decide how to interpret the answer based on the context. For example, should the answer be written as a decimal, a fraction, or a whole number with a remainder? Is the remainder the answer to the problem? Does the remainder affect the answer to the question? Should the remainder be disregarded when answering the question?
- Students will be able to determine reasonable answers to real-world and mathematical problems.
Work from previous grades that supports this new learning includes:
- Solve real-world and mathematical problems requiring addition, subtraction, multiplication and division of multi-digit whole numbers. Use various strategies, including inverse relationships between operations, the use of technology, and the context of the problem to assess the reasonableness of results;
- Recognize and generate equivalent decimals, fractions, mixed numbers, and improper fractions in various contexts;
- Solve real-world and mathematical problems requiring addition and subtraction of decimals, fractions, and mixed numbers, including those involving measurement, geometry and data;
- Consider the context in which a problem is situated to select the most useful form of the quotient for the solution and use the context to interpret the quotient appropriately;
- Estimate solutions to arithmetic problems in order to assess the reasonableness of results;
- Apply the commutative, associative and distributive properties and order of operations to generate equivalent numerical expressions to solve problems involving whole numbers;
- Represent real-world situations using equations and inequalities involving variables. Create real-world situations corresponding to equations and inequalities.
NCTM Standards:
Work flexibly with fractions, mixed numbers, and decimals to solve problems
- Build on prior knowledge from previous grade levels and everyday life;
- Use of decimals and fractions includes measurements and comparisons;
- Ensure solid understanding of context when deciding among differing representations for equivalency and moving flexibly between them;
Understand and use the associative, commutative, and distributive properties to simplify computations with integers, fractions, and decimals
- Use mathematical properties to simplify many computations involving fractions and decimals;
- Use common procedures to multiply and divide fractions and decimals efficiently and accurately;
Develop and analyze algorithms for computing with fractions, decimals, and integers and develop fluency in their use
- Develop own methods of computation and sharing results with class;
- Explain why methods chosen and subsequent solutions are reasonable;
- Compare and evaluate personal method with traditional algorithms;
Understand and use the inverse relationship of multiplication and division to simplify and solve problems
- Be mindful of the decision of when to multiply or divide when working with fractions, mixed numbers, or decimals;
- Increase understanding of division as being repeated subtraction rather than just a rote procedure of invert and multiply;
- Select appropriate methods and tools for computing with fractions and decimals from among mental computation, estimation, calculators or computers, and paper and pencil, depending on the situation, and apply the selected methods.
Learn when an exact answer or an estimate is needed;
Identify which computational method should be chosen;
Evaluate reasonableness of solution;
Increase mental computation and estimation.
Common Core State Standards (CCSS):
5BTB (Number And Operations In Base Ten) Perform operations with multi-digit whole numbers and with decimals to hundredths.
5NTB.7 Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
5NF (Number And Operations--Fractions) Use equivalent fractions as a strategy to add and subtract fractions.
5NF.2 Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers.
5NF.4 Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
5NF.6 Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
5NF.7 Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions.1
5NF.7.c Solve real world problems involving division of unit fractions by non-zero whole numbers and division of whole numbers by unit fractions, e.g., by using visual fraction models and equations to represent the problem.
6NS (Number System) Apply and extend previous understandings of multiplication and division to divide fractions by fractions.
6NS.1 Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem.
6NS.3 Fluently multiply and divide multi-digit decimals using the standard algorithm for each operation.
6RP (Ratios And Proportional Relationships) Understand ratio concepts and use ratio reasoning to solve problems.
6RP3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
6RP3.c Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.
7NS (Number System) Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers.
7NS.3 Solve real-world and mathematical problems involving the four operations with rational numbers.
Misconceptions
Student Misconceptions and Common Errors
- Students struggle to understand mathematical relationships in real-world problems and represent them with mathematical expressions;
- Students choose incorrect operations when solving problems;
- Students focus on getting answers and do not assess them for reasonableness.
Vignette
In the Classroom
In this vignette, students draw on their experiences with decimals and fractions to solve a problem involving volume.
Teacher: I plan to build a sandbox in the shape of a rectangular prism for my children. The base will be square, measuring 3 meters on each side. If I dump 4.5 cubic meters of sand into the sandbox and level it so that it has a uniform depth, how deep will the sand be?
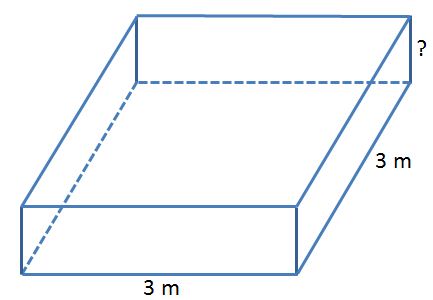
Student: I have no idea what a cubic meter is.
Teacher: What clues can you get from the words "cubic meter?"
Student: "Cube" and "meter." Maybe a cubic meter is a cube that measures 1 meter on each side.
Teacher: Yes, a cubic meter is a cube that is 1 meter long, 1 meter wide and 1 meter high. (Teacher uses hands to show approximate size.)
Student: A cubic meter of sand is a lot! I think we did a similar problem last year. It had something to do with volume.
Teacher: Why do you say that?
Student: Well, I remember stacking cubes to find the volume of a rectangular prism.
Teacher: Yes, volume is the amount needed to fill a three-dimensional space. What did you do?
Student: First we built a layer of cubes in the shape of the rectangle at the bottom. Then we continued to add layers until the rectangular prism was the right height. The total number of cubes needed to build the rectangular prism was its volume.
Teacher: How did you find the total number of cubes?
Student: At first, we counted the cubes one by one. But then we found a faster way. Since every layer had the same number of cubes, it was faster to multiply the number of cubes in each layer by the number of layers.
Teacher: Interesting. It would be helpful if you showed the class an example of this strategy. How would you use it to find the volume of a rectangular prism that measures 3 units wide, 2 units long and 4 units high?
Student: First I would find the number of cubes in the bottom layer. Its base is a rectangle that measures 3 x 2, so I would need 6 cubes for the bottom layer. The height of the rectangular prism is 4 units, which means it has 4 layers. Every layer has the same number of cubes. 6 x 4 = 24, so 24 cubes are needed to build this rectangular prism. Its volume is 24 cubic units.
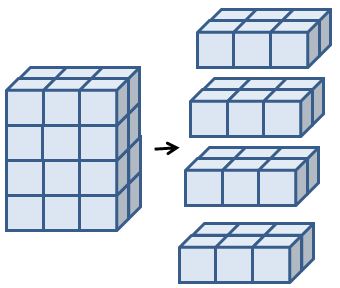
Teacher: Nice explanation! You found the number of cubes in the bottom layer by multiplying the rectangle's length by its width. When we multiply a rectangle's length by its width, what are we actually determining?
Student: Its area!
Teacher: Exactly. The area of any rectangle, or number of square units needed to cover it, can be found by multiplying its length by its width. For this rectangular prism, the area is 3 • 2 or 6 square units. The area of the rectangular base, 6 square units in this case, tells us that 6 cubes are needed to build the bottom layer. Next you multiplied the number of cubes in each layer by the number of layers, or height of the prism. 6 • 4 = 24, so the volume of this rectangular prism is 24 cubic units. Perhaps you've seen the formula V = B • h, where V represents volume, B represents base area, and h represents height. This formula is another way to write down the strategy we just used to find the volume of the rectangular prism. B, the base area, tells us the number of cubes in the bottom layer; h, the height, tells us the number of layers. By multiplying them together, we find the total number of cubes, or volume. But let's get back to the sandbox problem. Our task is to find out how deep the sand will be if we dump in 4.5 m3 of sand and level the sand to a uniform depth. What are some things we know about the volume of the sandbox?
Student: I think every layer will have 9 cubes.
Teacher: How do you know that?
Student: Because the base is a square that measures 3 meters on each side and 3 ![]() 3 = 9. Since 9 squares are needed to cover the base, then every layer will have 9 cubes.
3 = 9. Since 9 squares are needed to cover the base, then every layer will have 9 cubes.
Teacher: Good reasoning. What else do you know?
Student: Well, if there are 9 cubes in every layer, then 9 • h = 4.5. We should be able find the number of layers, or depth (h), by dividing 4.5 by 9.
Teacher: How will you find that quotient?
Student: Well, I have to find the number of 9s in 4.5, or 4.5 ÷ 9, and I see that 4.5 is a decimal. I know that when I multiplied by decimals, I thought about how 4.5 is 45 divided by 10. So maybe I can divide 45 by 9 and then divide the quotient by 10. Let me try and see if it makes sense: 45 ÷ 9 = 5, so 4.5 ÷ 9 = 0.5.
Teacher: Good. Now how can you decide if your answer makes sense?
Student: Well, I know that 4.5 is less than 9, so if I divide 4.5 into 9 groups, there must be fewer than 1 in a group. And 0.5 is less than 1, so that is reasonable.
Teacher: Your answer is reasonable, but I'm not convinced that you have a good sense of whether your answer is correct. Let's see if we can think of another way to solve the sandbox problem. We have to find 4.5 divided by 9. Let's use what we know about division and fractions. Think of the whole-number division problem 45 ÷ 9. How would you write that as a fraction?
Student: $\frac{45}{9}$
Teacher: That's right. You can right any division problem as a fraction with the dividend in the numerator and the divisor in the denominator. So we can write 4.5 ÷ 9 as $\frac{4.5}{9}$. We can write any type of number as the numerator and denominator of a fraction - whole numbers, decimals, or even other fractions. Once we have written the quotient as a fraction, we can treat the number like any other fraction. For example, we can create an equivalent fraction by multiplying by some fraction form of 1, which is the same as multiplying the numerator and denominator by the same number. Is there a fraction form of 1 that would you multiply $\frac{4.5}{9}$ by to make it easier to find a quotient?
Student: I might multiply by $\frac{10}{10}$. That will make 4.5 a whole number, and then the problem is just like a whole-number division problem.
Teacher: That is a good choice. So multiply by $\frac{10}{10}$ to find an equivalent fraction that does not have a decimal in it.
Student: $\frac{4.5}{9}\times \frac{10}{10}=\frac{4.5\times 10}{9\times 10}=\frac{45}{90}$.
Teacher: So the quotient of 4.5 ÷ 9 is the same as the quotient of 45 ÷ 90.
Student: Wait. I see the answer now. I know that 45 is half of 90, so $\frac{45}{90}=\frac{1}{2}$. But I also know that $\frac{1}{2}$ = 0.5, so 4.5 ÷ 9 = 0.5. That's the same answer I got before!
Teacher: What would you have done if the problem had been 4.6 ÷ 8?
Student: $\frac{4.6}{8}\times \frac{10}{10}=\frac{4.6\times 10}{8\times 10}=\frac{46}{80}$. I know that 2 is a common factor of the numerator and denominator, so the fraction can be simplified: $\frac{46\div 2}{80\div 2}=\frac{23}{40}$.
Teacher: The original sandbox problem gave the volume in decimal form, so we should probably also express the depth in decimal form. How can you find the decimal for $\frac{23}{40}$?
Student: Divide 23 by 40.
Teacher: Yes. Go ahead and divide. Then I want to see how you worked the problem from the very beginning.
Student: Here's my work.
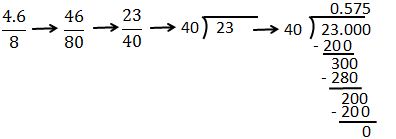
Teacher: Your thinking is clearly communicated. Nicely done! How do you know that 0.575 is a reasonable answer?
Student: The answer should be a little more than $\frac{1}{2}$, because $\frac{20}{40}$ is $\frac{1}{2}$, and we have $\frac{23}{40}$. The decimal for $\frac{1}{2}$ is 0.5, or 0.500, and 0.575 is a little more than that.
Teacher: Good reasoning and well said!
Resources
Teacher Notes
Students who struggle to understand relationships in real-world problems will benefit from using a visual approach to show the relationships. The Singapore Bar Model is one example of a visual approach. It utilizes four models to show relationships.
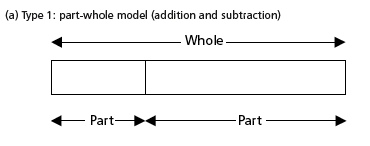
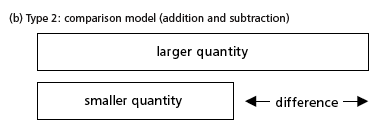
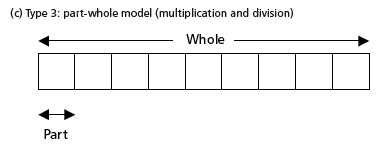

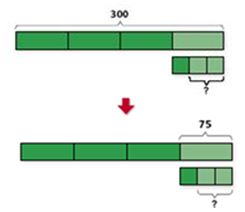
- Utilizing a visual approach to model relationships, such as the Singapore Bar Model, will also support students in selecting the correct operation to solve problems as it makes explicit which relationships involve addition and subtraction and which relationships involve multiplication and division. Below are examples of how a bar model can be used to enable students to grasp concepts visually.
Example: Martha made 300 cookies. She sold $\frac{3}{4}$ of them and gave $\frac{1}{3}$ of the remainder to her neighbor. How many cookies did she have left?
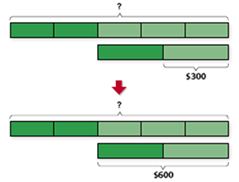
Example: Mr. Anderson gave $\frac{2}{5}$ of his money to his wife and spent $\frac{1}{2}$ the remainder. If he had $300 left, how much money did he have at first?
- Students will benefit from linking the language of the problem to its visual representation. Note the following example from Singapore Math. Example: There are 20% more girls than boys in an art club. If there are 45 boys in the art club, how many girls are there?
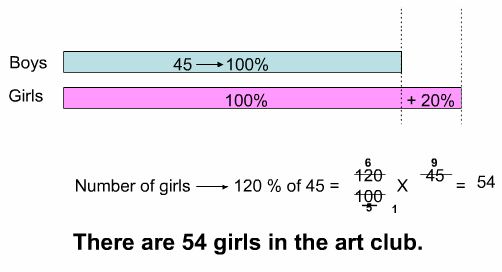
- As students work on real-world problems, their focus tends to be more on getting answers than on using problem-solving skills and strategies. As teachers, it is essential to encourage the problem-solving process. One example of the problem-solving process comes from Dr. George Polya's book How to solve it (1945).
Understand the Problem (Recognize what is asked for),
Devise a plan (Responding to what is asked for),
Carry out the plan (Developing the result of the response), and
Look back. (Checking... what does the result tell me?).
- One key component of any problem-solving process involves assessing results for reasonableness. By modeling and making explicit the steps of the process, checking the results for reasonableness will soon become routine.
- By providing related clusters of problems, teachers can help students distinguish between contexts and solution approaches. The cluster of problems below can be used to emphasize similar contexts, but different operations. Encourage students to think about whether their answers should be greater than or less than the numbers in the problem. For example, in problem 3, students should think that they are dividing 12 by a number less than 1, so they know the answer should be greater than 12. In problem 4, students could think that they are pouring 12 servings, but each serving is less than 1 liter, so the total amount of juice is less than 12 liters.

- This cluster of problems can be used to emphasize similar contexts and same operation, but different numbers. These problems give teachers the opportunity to guide students to look for relationships in the problem by encouraging them to compare the solution with the numbers in the problem and explain why the relationship exists. After many experiences with problem pairs like these, students should be able to explain that dividing a number (the dividend) by a number less than 1 (the divisor), the quotient is greater than the number that was divided (the dividend). Also, when dividing a number (the dividend) by a number greater than 1 (the divisor), the quotient is less than the number that was divided (the dividend). As they progress through their mathematics education, they will discover that these ideas are true only when the numbers are all positive.

- This cluster of problems can be used to emphasize that you can choose to use decimals or fractions to solve a problem. Teachers can ask students to consider whether they would use decimals or fractions to solve the problems. Students should realize that in the first problem, $\frac{1}{4}$ can be written as 0.25 and 1.8 can be written as $1\frac{8}{10}$. In the second problem, students should realize that four tenths can be written as 0.4 or $\frac{4}{10}$ = $\frac{2}{5}$.

In this lesson, use an airport theme to investigate numbers and solve problems.
In this lesson, students organize and plan a luncheon for the entire class.
In this lesson, students work with decimals, fractions, and percentages in the context of baseball statistics.
In these two lessons, students participate in activities in which they develop number sense in and around the shopping mall. The first lesson is appropriate for grades 3-5, while the second lesson is appropriate for grades 6-8. Both grade-level activities deal with size and space, estimation, measurement, and applications involving percent.
Additional Instructional Resources
This website provides problems at four levels of difficulty.
reciprocal: the multiplicative inverse of a number; in other words, a reciprocal is a number that you multiply by so the resulting product equals 1. Example: The reciprocal of $\frac{3}{5}$ is $\frac{5}{3}$ because $\frac{3}{5}$ x $\frac{5}{3}$ = 1.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What problems can be clustered to emphasize similar contexts and different operations?
- What problems can be clustered to emphasize similar contexts, same operations, and different numbers?
- What problems can be used to emphasize that you can choose decimals or fractions to solve a problem?
- What evidence shows that students use a problem-solving plan?
- What evidence shows that students routinely use estimation to check their answers and refine their computational skills?
Materials
This website explains the use of model drawing to help students comprehend and convert problem situations into relevant mathematical expressions to solve them.
- Singapore Math: Simple or Complex
This article discusses the bar model approach to help students think symbolically and solve hard problems.
- NCTM A Research Companion to Principles and Standards for School Mathematics (Details about this resource can be found in the References section.)
Chapter 18, Impact of Reform on Representations, pp. 263-264.
Kaput, J. (1989). Linking representations in the symbol system of algebra. In C. Kieran & S.Wagner (Eds.), A research agenda for the learning and teaching of algebra. Hillsdale, NJ: Lawrence Erlbaum.
Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
South Carolina State Department of Education. Math Curriculum Standards. N.p., n.d. Web. 1 Apr. 2011. Retrieved from http://ed.sc.gov/agency/Standards-and-Learning/Academic-Standards/old/c….
Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
National Council of Teachers of Mathematics. (2010). Focus in grade 6 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics, Inc.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
New Jersey Mathematics Curriculum Framework. The official web site for the state of New Jersey. N.p., Web. 1 Apr. 2011. Retrieved from http://www.state.nj.us/education/frameworks/math/.
Assessment
(DOK Level 2)
1. Gina has $48. She spent $\frac{1}{4}$ of the money on a CD, and $\frac{3}{8}$ on a sweatshirt. How many dollars did she spend?
Answer: $30
(DOK Level 2)
2. Bailey feeds dogs for the Humane Society. Each dog gets $\frac{1}{4}$ pound of food per day. How many dogs can Bailey feed with $5\frac{2}{3}$ pounds of food?
a) 23 dogs b) 22 dogs c) 21 dogs d) 20 dogs

Answer: b.
Differentiation
This website provides a visual approach to problem-solving. Bar models are used to represent relationships and unknowns, helping students visualize the problems more clearly. Problems are available for multiple grade levels and varying levels of difficulty.
In these two lessons, students participate in activities in which they develop number sense in and around the shopping mall. The first lesson is appropriate for grades 3-5, while the second lesson is appropriate for grades 6-8. Both grade-level activities deal with size and space, estimation, measurement, and applications involving percent.
- Provide a multiplication chart to assist students who are struggling with basic multiplication facts, while encouraging them to master the facts.
This website provides a visual approach to problem-solving. Bar models are used to represent relationships and unknowns, helping students visualize the problems more clearly. Problems are available for multiple grade levels and varying levels of difficulty.
- Students will benefit from linking the language of the problem to its visual representation. Note the following example from Singapore Math. Example: There are 20% more girls than boys in an art club. If there are 45 boys in the art club, how many girls are there?
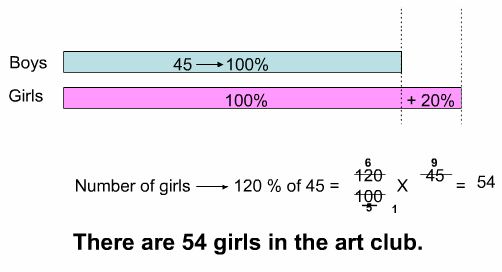
- Use graphic organizers such as the Frayer model shown below, for vocabulary development.
This website provides enriched opportunities for problem solving.
In this lesson, students use fractions and customary measurements to alter recipes to serve large numbers of people. Operations with decimals are used to determine profit from a catering job.
In this lesson, students compute with decimals to solve problems encountered by people involved in law enforcement careers.
The sum of the numbers 4 and $1\frac{1}{3}$ is the same as the product of 4 and $1\frac{1}{3}$;
that is to say 4 + $\frac{4}{3}$ = 4 × $\frac{4}{3}$. What other numbers have the sum equal to the product and can this be so for any whole numbers? What relationship must exist between the numbers?
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: (descriptive list) |
Teachers are: (descriptive list) |
|
using a process to solve problems; e.g., understand, plan, solve, check. |
modeling and making explicit each step of the problem-solving process. |
|
drawing visual representations of situations to discover relationships |
using visual representations to scaffold to abstract representations. |
|
choosing correct operations to solve problems. |
posing clusters of problems with similar contexts that require different operations. |
|
predicting whether their answers will be greater or less than the numbers in the problems. |
posing clusters of problems with similar contexts, same operation, and different numbers. |
|
solving a variety of problems that require arithmetic of fractions and decimals. |
posing clusters of real-world problems for students to choose the use of decimals or fractions. |
|
assessing answers for reasonableness. |
requiring students to look back and ask if their solution makes sense in the context of the problem. |
|
applying a variety of problem-solving strategies previously used with whole numbers to fractions and decimals. |
using students' previous problem-solving experiences as a foundation to build upon for experiences with fractions and decimals. |
|
making inferences, justifying conclusions, and sharing their thinking with others as they solve real-world problems. |
assisting students in making problem solving connections between previously learned concepts and current solutions. |
Parent Resources
- Singapore Math Problems
This website provides a visual approach to problem-solving. Bar models are used to represent relationships and unknowns, helping students visualize the problems more clearly. Problems are available for multiple grade levels and varying levels of difficulty.
