Cluster One: Planning & Assessment (Interpreting, Responding)

 

 

Introduction 

In order to clarify pathways to implementation of the mathematics teaching practices outlined in Principles to Actions (NCTM, 2014), the National Council of Teachers of Mathematics (NCTM) created the Taking Action series, in which they provide tools to aid teachers in further development and reflection around these 8 instructional practices. NCTM also organized these practices into a Mathematics Teaching Framework (2019) to help mathematics educators discern the connections between these practices within a classroom setting. Establishing goals to focus learning creates a foundation for all decisions regarding planning and implementation of mathematics instruction. Selecting problem solving tasks that align to these goals can help students develop a conceptual understanding from which fluency can be developed (Berry, 2019).

Merging Models

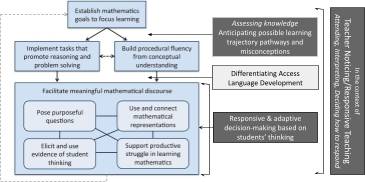
The models of planning and assessment presented here overlap and differ in significant ways.  Blending the two together strengthens the planning and assessment process. Figure One addresses anticipating students’ thinking teachers need to bring to the planning process (Empson & Jacobs, 2021, p.667/652, Hiebert, et al., 1997, Simon, 1995). Such anticipation, including planning for misconceptions, influences one’s ability to decide how to respond in the midst of instruction. Adding this disposition to the Mathematics Teaching Framework establishes an approach to teaching that empowers students in developing the critical thinking skills, voice, and depth of conceptual and procedural knowledge needed for forward momentum in learning further mathematical ideas.  This merged model is the focus around which the materials in all four clusters are centered.

---

Figure One: System of Instruction - Adapted from Hiebert, et al, 1997

---

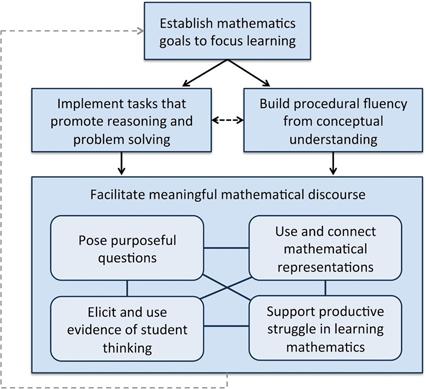
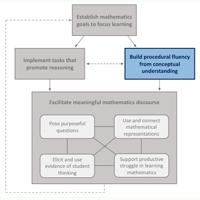
Figure Two: Mathematics Teaching Framework - NCTM, Taking Action Series, 2017

---

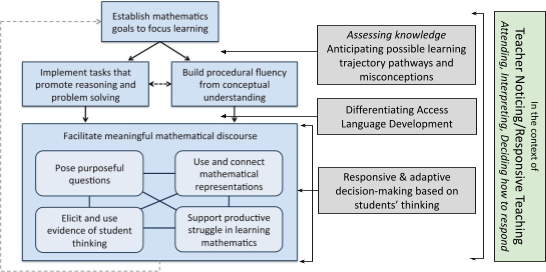
Figure Three: A System of Practice. Created by merging the System of Instruction model (Hiebert, et al. 1997), the Mathematics Teaching Framework (NCTM, Taking Action Series, 2017), and Teacher Noticing Skills/Responsive Teaching  research (Jacobs, et al., 2010, Richards & Robertson, 2016)

---

Defining Assessment

Assessment is often confused with the instruments used to collect data; a unit test, an exit slip. Those are instruments to collect assessment data. Assessment is an act of interpretation and the subsequent decision making and feedback resulting from that interpretation. Assessment is built on the information gathered before, during, and after the instructional task(s) are undertaken by the learners. It is the knowledge that the teacher has of the students’ level of developmental understanding of the mathematical concepts based on progressions of strategies, the level of efficiency and fluency by which the strategies were enacted, and the level of precision and accuracy of the work. This involves interpreting students’ thinking and using that information to decide how to plan, adjust, adapt, elicit, differentiate, scaffold, etc. The data is collected prior to students engaging with the task (prior knowledge inventory), while the students are working (formative assessment), and after a unit is completed (summative assessment). The assessment data is the feedback needed to inform instruction in-the-moment, to be used to launch the next day’s lesson, to differentiate a lesson to allow access points for all students, and to provide data for additional support to further learning. It is also the feedback provided to students so that they can monitor their own progress and decide next steps.  Instruction and formative assessment in particular are so intertwined that they are at times indistinguishable (Levi & Ambrose, 2018). Having an organized framework by which to interpret students’ thinking and resulting artifacts is key to grounding instructional decision making. Only then does the data become useful. 

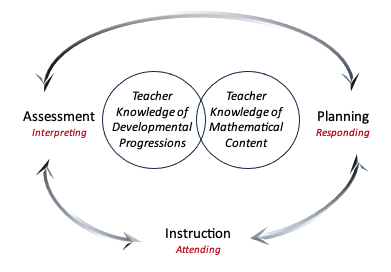
Figure Four: The Assessment/Planning Cycle

Asset/Strength-based Planning & Assessment - Conditions for Accessing Formative Assessment Data 

An asset-based perspective and approach to teaching and learning is anchored on what students are doing rather than what students can’t do. Students bring their prior knowledge and cultural identities to the classroom. These are assets, strengths, not deficits. They know something. Students who are multilingual have ways of expressing mathematical ideas that translate differently into English. Understanding these and allowing students to access these ways of expression are assets, not deficits. Accessing student thinking in the midst of instruction as well as in how the learning artifacts collected from a lesson are reviewed later frames the kind and richness of assessment data. The deficit model tends to assess correctness, fluency, and what students lack in understanding. An asset/strength based assessment views students on what they do understand even if only partially understood. Knowing what they do know, allows the teacher to be more strategic in interpreting the student’s understanding and in deciding how to respond. 

Learning is relational. The more students feel teachers and support staff around them actually like them and genuinely listen to them, the more they will learn (Battey, Neal & Hunsdon, 2018).  This setting of the emotional tone in the classroom along with how teachers frame students’ mathematical abilities are conditions that allow students to express their thinking. Key in getting students emotionally and intellectually ready to risk sharing their thinking is in how student contributions are acknowledged and how language and culture are accepted and addressed. Leahy et al. (2011) identified five key strategies in their assessment-for-learning model. These strategies worked across content areas and grade levels. 

 ‘Activating students as owners of their own learning’ and ‘activating students as instructional resources for one another’ overlap distinctly with the relational-based working environments of Battey et al. (2018) and Levi and Ambrose (2018) note as the conditions for accessing quality formative assessment centered on student thinking. Knowing one is capable of thinking mathematically allows the realization that one can be in charge of one’s learning. Related, but addressed under Cluster Two: Instruction, are asset-based pedagogies. These combined practices address equity and access issues for all students from all backgrounds are able to grow mathematically. 

Cultural Awareness

Minnesota is the current, future, and ancestral home of the Dakota and Anishinaabe/Ojibwe people. It is the current and future home of immigrants from around the world, many of whom are the descendents of indigenous populations of Central and South America. Incorporating the cultural perspectives of students influences how students learn and achieve. Incorporating Dakota and Anishinaabe/Ojibwe perspectives is law in Minnesota. We must all do the hard work of coming to levels of understanding of how this influences planning, assessment, and instruction. 

• Minnesota Native American Essential Understandings For Educators
• A Guide to Reliable Native American-Related Teaching Resources
• UnderstandNativeMN.org

The Planning Process

There are common threads among the work of those who have followed Simon’s (1995) original articulation of ‘hypothetical learning trajectories.’ What comes first is to establish clear mathematical goals to focus learning. Backwards curriculum design principles (Wiggins & McTighe, 1998; Bowen, 2017) discuss that once the mathematical goals have been identified, three stages of planning follow. They include the identification of desired results, the determination of acceptable evidence, and only then comes the planning of the learning tasks and instruction. Others start with the same premise; mathematical goals first, followed by identifying what understanding looks and sounds like (assessment identifiers). Hiebert, et al. (1997) then describes identifying the potential learning pathways/trajectories – including any possible misconceptions – that students might take while engaging with the targeted mathematics. Once instruction begins, and students engage in the learning, adaptations potentially need to be made to the lesson plan. “Tasks are selected purposefully, but the sequence can be revised” (p. 34). This is a core element of responsive teaching.

Establish Mathematics Goals to Focus Learning (Page 16, Principles to Action, NCTM, 2014)

What are teachers doing?

• Establishing clear goals that articulate the mathematics that students are learning as a result of instruction in a lesson, over a series of lessons, or throughout a unit.
• Identifying how the goals fit within a mathematics learning progression.
• Discussing and referring to the mathematical purpose and goal of a lesson during instruction to ensure that students understand how the current work contributes to their learning.
• Using the mathematics goals to guide lesson planning and reflection and to make in-the-moment decisions during instruction.

What are students doing?

• Engaging in discussions of the mathematical purpose and goals related to their current work in the mathematics classroom (e.g., What are we learning? Why are we learning it?)
• Using the learning goals to stay focused on their progress in improving their understanding of mathematics content and proficiency in using mathematical practices.
• Connecting their current work with the mathematics that they studied previously and seeing where the mathematics is going.
• Assessing and monitoring their own understanding and progress toward the mathematics learning goals. (NCTM, 2014, p. 16)

Access additional standards and related documents

---

 
The Assessment Process

As previously presented, assessment is the act of interpretation and the subsequent decision making and feedback resulting from the interpretation of where one’s students are at in the process of learning the mathematical concepts at hand. Determining what constitutes evidence of conceptual understanding of the selected mathematical goals and objectives is central to the assessment process. This is done before tasks are selected. Instructional tasks are shaped around how the evidence might best reveal student understanding. Monitoring and assessing the emerging procedural fluency is integrated into the process. Determining if the student's understanding of the mathematics is at the initial and often messy stage, or at intermediate or refining stages influences the type of assessment data one is looking for/implementing and therefore which tasks are best suited for drawing out student thinking. 

Once a lesson has started, assessing in the moment (attending and interpreting) and deciding how to respond through adjustments to the lesson, questions asked, the sequence of shared student work, etc. are all how assessment and instruction are intertwined. From the student artifacts – physical, drawn, written, gestured, and verbalized – the interpretation of students’ progress shapes the planning for the next day’s lesson. The assessment process is iterative: planning, in-the-moment adjustments, interpretation of artifacts, planning… This is another core element of responsive teaching. 

---

To Elicit and Use Evidence of Student Thinking (Page 56, Principles to Action, NCTM, 2014)

Notice the placement of assessment in the Mathematics Teaching Framework. This captures the legitimate in-the-moment assessment (attending & interpreting) that occurs in the midst of a lesson. The placement of assessment in the merged model above is situated within the planning process as well as in-the-moment assessment. Assessment, meaning the interpretation of data, permeates the whole planning-learning cycle. 

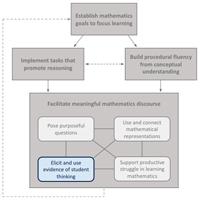
What are teachers doing?

• Identifying what counts as evidence of student progress toward mathematics learning goals.
• Eliciting and gathering evidence of student understanding at strategic points during instruction.
• Interpreting student thinking to assess mathematical understanding, reasoning, and methods.
• Making in-the-moment decisions on how to respond to students with questions and prompts that probe, scaffold, and extend.
• Reflecting on evidence of student learning to inform the planning of next instructional steps.

What are students doing?

• Revealing their mathematical understanding, reasoning, and methods in written work, physical artifacts, non-verbal gestures, and classroom discourse.
• Reflecting on mistakes and misconceptions to improve their mathematical understanding.
• Asking questions, responding to, and giving suggestions to support the learning of their classmates.
• Assessing and monitoring their own progress toward mathematics learning goals and identifying areas in which they need to improve.

Access additional MDE assessment documents and related developmental learning frameworks 

 

---

Implement Tasks that Promote Reasoning and Problem Solving (Page 24, Principles to Action, NCTM, 2014)

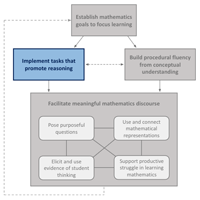
What are teachers doing?

• Motivating students’ learning of mathematics through opportunities for exploring and solving problems that build on and extend their current mathematical understanding.
• Selecting tasks that provide multiple entry points through the use of varied tools and representations.
• Posing tasks on a regular basis that require a high level of cognitive demand.
• Supporting students in exploring tasks without taking over student thinking.
• Encouraging students to use varied approaches and strategies to make sense of and solve tasks.
  

What are students doing?

• Persevering in exploring and reasoning through tasks.
• Taking responsibility for making sense of tasks by drawing on and making connections with their prior understanding and ideas.
• Using tools and representations as needed to support their thinking and problem solving.
• Accepting and expecting that their classmates will use a variety of solution approaches and that they will discuss and justify their strategies to one another. (NCTM, 2014, p. 24)

Access additional explanations and resources on task selection

 

---

Build Procedural Fluency from Conceptual Understanding (Page 47-48, Principles to Action, NCTM, 2014)

What are teachers doing?

• Providing students with opportunities to use their own reasoning strategies and methods for solving problems.
• Asking students to discuss and explain why the procedures that they are using work to solve particular problems.
• Connecting student-generated strategies and methods to more efficient procedures as appropriate.
• Using visual models to support students’ understanding of general methods.
• Providing students with opportunities for distributed practice of procedures.
  

What are students doing?

• Making sure that they understand and can explain the mathematical basis for the procedures that they are using.
• Demonstrating flexible use of strategies and methods while reflecting on which procedures seem to work best for specific types of problems.
• Determining whether specific approaches generalize to a broad class of problems.
• Striving to use procedures appropriately and efficiently. (NCTM, 2014, pp. 47-48)

Access additional resources related to conceptual understanding and procedural fluency

 

---

Resources

• Colorado Department of Education Sample Curriculum - High Impact Instructional Strategies
• All Students, All Standards (ASAS) Institute on Instructional Shifts
• Achieve the Core - High Impact Instructional Strategies in Mathematics

 

---

Return to the Mathematical Practices Overview Page

---

References

Battey, D., Neal, R.A., and Hunsdon, J. (2018). Strategies for caring mathematical interactions. Teaching Children Mathematics. 24(7), 432-440.

Carpenter, T.P. (1989). Teaching as problem solving, In R.I. Charles & E.A. Silver, Eds., The Teaching and Assessing of Mathematical Problem Solving. pp. 187-202. National Council of Teachers of Mathematics: Reston, VA.

Hiebert, J., Carpenter, T.P., Fennema, E., Fuson, K. C., Wearne, D., Murray, H. Olivier, A., and Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. pp. 29-41. Heinemann Press: Portsmouth, NH.

Huinker, D. (2018). Principles to actions: Moving to a framework for teaching mathematics. Teaching Children Mathematics, 25(3), 133-136.

Huinker, DeAnn, and Victoria Bil. (2017). Taking Action: Implementing effective mathematics teaching practices in kindergarten– grades 5. Taking Action Series. National Council of Teachers of Mathematics.

Jacobs, V.R. and Empson, S.B. (2021). Profiles of teachers’ expertise in professional noticing of children’s mathematical thinking. In Olanoff, D., Johnson, K., & Spitzer, S. Proceedings of the forty-third annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Philadelphia, PA.

Jacobs, V.R., Lamb, L.L.C., Phillipps, R.A. (2010) Professional Noticing of Children’s Mathematical Thinking. Journal for Research in Mathematics Education. 41(2), 169–202.

Leahy, S., Lyon, C., Thompson, M., and Wiliam, D. (2011). Classroom Assessment: Minute-by-minute, Day-by-day. ASC. Retrieved from: https://pdo.ascd.org/LMSCourses/PD11OC101M/media/FA_M03_Reading_02_Classroom-Assessment.pdf 

Levi, L. and Ambrose, R. (2018). Cognitively guided instruction and formative assessment. In A Fresh Look at Formative Assessment in Mathematics Teaching, E.L. Silver and V.L. Mills, Eds. pp 41-60. NCTM: Reston, VA. 

National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. National Council of Teachers of Mathematics.

National Council of Teachers of Mathematics (2017). Taking action: Implementing Effective Mathematics Teaching Practices. https://www.nctm.org/store/takingaction/ NCTM: Reston, VA.

Richards, J. and Richardson, A.D., (2015). A Review of the Research on Responsive Teaching. In A. D. Robertson, R. E. Scherr, and D. Hammer (Eds.) Science and Mathematics Responsive Teaching in Science and Mathematics (pp.36-55), Routledge, London.

Smith, M. S., & Stein, M. K. (2011). 5 practices for orchestrating productive mathematics discussions. National Council of Teachers of Mathematics and Corwin Press.