9.4.3A Counting Procedures
Select and apply counting procedures, such as the multiplication and addition principles and tree diagrams, to determine the size of a sample space (the number of possible outcomes) and to calculate probabilities.
For example: If one girl and one boy are picked at random from a class with 20 girls and 15 boys, there are 20 × 15 = 300 different possibilities, so the probability that a particular girl is chosen together with a particular boy is $\frac{1}{300}$.
Overview
Standard 9.4.3 Essential Understandings
Life is a school of probability. - Walter Bagehot
Students have calculated probabilities to solve real world problems in the form of experimental probabilities, probability as a fraction of sample space or area, and used random number generators to conduct simulations. This standard builds on this knowledge in that students learn counting strategies and more advanced probability concepts such as intersections, unions, complements, and conditional probability. Students work on "formalizing probability procedures and language, creating and interpreting probability distributions to solve real world problems, implementing simulation techniques, and presenting cohesive arguments in oral and written form." (Minnesota Math Frameworks, 1997, Randomness and Uncertainty, P. 19.) Students investigate probability problems with technology through simulations. Virtually all jobs require decision-making capabilities under uncertain conditions. Technology enables large amounts of data to be analyzed, but it is humans who must make sense of the data.
All Standard Benchmarks
9.4.3.1 Select and apply counting procedures, such as the multiplication and addition principles and tree diagrams, to determine the size of a sample space (the number of possible outcomes) and to calculate probabilities.
For example: If one girl and one boy are picked at random from a class with 20 girls and 15 boys, there are 20 × 15 = 300 different possibilities, so the probability that a particular girl is chosen together with a particular boy is 1/300.
9.4.3.2 Calculate experimental probabilities by performing simulations or experiments involving a probability model and using relative frequencies of outcomes.
9.4.3.3 Understand that the Law of Large Numbers expresses a relationship between the probabilities in a probability model and the experimental probabilities found by performing simulations or experiments involving the model.
9.4.3.4 Use random numbers generated by a calculator or a spreadsheet, or taken from a table, to perform probability simulations and to introduce fairness into decision making.
For example: If a group of students needs to fairly select one of its members to lead a discussion, they can use a random number to determine the selection.
9.4.3.5 Apply probability concepts such as intersections, unions and complements of events, and conditional probability and independence, to calculate probabilities and solve problems.
For example: The probability of tossing at least one head when flipping a fair coin three times can be calculated by looking at the complement of this event (flipping three tails in a row).
9.4.3.6 Describe the concepts of intersections, unions and complements using Venn diagrams. Understand the relationships between these concepts and the words AND, OR, NOT, as used in computerized searches and spreadsheets.
9.4.3.7 Understand and use simple probability formulas involving intersections, unions and complements of events.
For example: If the probability of an event is p, then the probability of the complement of an event is 1 - p; the probability of the intersection of two independent events is the product of their probabilities. Another example: The probability of the union of two events equals the sum of the probabilities of the two individual events minus the probability of the intersection of the events.
9.4.3.8 Apply probability concepts to real-world situations to make informed decisions.
For example: Explain why a hockey coach might decide near the end of the game to pull the goalie to add another forward position player if the team is behind. Another example: Consider the role that probabilities play in health care decisions, such as deciding between having eye surgery and wearing glasses.
9.4.3.9 Use the relationship between conditional probabilities and relative frequencies in contingency tables.
For example: A table that displays percentages relating gender (male or female) and handedness (right-handed or left-handed) can be used to determine the conditional probability of being left-handed, given that the gender is male.
Benchmark Group A
Benchmark 9.4.3.1 Select and apply counting procedures, such as the multiplication and addition principles and tree diagrams, to determine the size of a sample space (the number of possible outcomes) and to calculate probabilities.
What students should know and be able to do [at a mastery level] related to this benchmark:
Students should be able to use counting techniques (e.g. tree diagrams, multiplication principle, and addition principle) and multiple representations to solve probability problems.
Work from previous grades that supports this new learning includes:
- Students should be familiar with using the 0-1 scale as a measure of probability.
- Students have begun to develop counting techniques and the ability to list outcomes through a variety of strategies including tree diagrams, graphs, tables, and charts.
- Students have experience with relative frequency and theoretical probability.
NCTM Standards
Data Analysis and Probability Standards
3. develop and evaluate inferences and predictions that are based on data
- understand how sample statistics reflect the values of population parameters and use sampling distributions as the basis for informal inference
4. understand and apply basic concepts of probability
- understand the concepts of sample space and probability distribution and construct sample spaces and distributions in simple cases
- use simulations to construct empirical probability distributions
- compute and interpret the expected value of random variables in simple cases
- understand the concepts of conditional probability and independent events
- understand how to compute the probability of a compound event.
Common Core State Standards (CCSS)
S-IC: Making Inferences and Justifying Conclusions
Understand and evaluate random processes underlying statistical experiments
2. Decide if a specified model is consistent with results from a given data-generating process, e.g., using simulation. For example, a model says a spinning coin falls heads up with probability 0.5. Would a result of 5 tails in a row cause you to question the model?
S-CP: Conditional Probability and the rules of Probability
Understand independence and conditional probability and use them to interpret data
1. Describe events as subsets of a sample space (the set of outcomes) using characteristics (or categories) of the outcomes, or as unions, intersections, or complements of other events ("or," "and," "not").
2. Understand that two events A and B are independent if the probability of A and B occurring together is the product of their probabilities, and use this characterization to determine if they are independent.
3. Understand the conditional probability of A given B as P(A and B)/P(B), and interpret independence of A and B as saying that the conditional probability of A given B is the same as the probability of A, and the conditional probability of B given A is the same as the probability of B.
4. Construct and interpret two-way frequency tables of data when two categories are associated with each object being classified. Use the two-way table as a sample space to decide if events are independent and to approximate conditional probabilities. For example, collect data from a random sample of students in your school on their favorite subject among math, science, and English. Estimate the probability that a randomly selected student from your school will favor science given that the student is in tenth grade. Do the same for other subjects and compare the results.
5. Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. For example, compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer
Use the rules of probability to compute probabilities of compound events in a uniform probability model
6. Find the conditional probability of A given B as the fraction of B's outcomes that also belong to A, and interpret the answer in terms of the model.
7. Apply the Addition Rule, P(A or B) = P(A) + P(B) - P(A and B), and interpret the answer in terms of the model.
8. (+) Apply the general Multiplication Rule in a uniform probability model, P(A and B) = P(A)P(B|A) = P(B)P(A|B), and interpret the answer in terms of the model.
9. (+) Use permutations and combinations to compute probabilities of compound events and solve problems.
S-MD: Using Probability to make decisions
Calculate expected values and use them to solve problems
1. (+) Define a random variable for a quantity of interest by assigning a numerical value to each event in a sample space; graph the corresponding probability distribution using the same graphical displays as for data distributions.
2. (+) Calculate the expected value of a random variable; interpret it as the mean of the probability distribution.
3. (+) Develop a probability distribution for a random variable defined for a sample space in which theoretical probabilities can be calculated; find the expected value. For example, find the theoretical probability distribution for the number of correct answers obtained by guessing on all five questions of a multiple-choice test where each question has four choices, and find the expected grade under various grading schemes.
4. (+) Develop a probability distribution for a random variable defined for a sample space in which probabilities are assigned empirically; find the expected value. For example, find a current data distribution on the number of TV sets per household in the United States, and calculate the expected number of sets per household. How many TV sets would you expect to find in 100 randomly selected households?
Use probability to evaluate outcomes of decisions
5. (+) Weigh the possible outcomes of a decision by assigning probabilities to payoff values and finding expected values.
a. Find the expected payoff for a game of chance. For example, find the expected winnings from a state lottery ticket or a game at a fast- food restaurant.
b. Evaluate and compare strategies on the basis of expected values. For example, compare a high-deductible versus a low-deductible automobile insurance policy using various, but reasonable, chances of having a minor or a major accident.
6. (+) Use probabilities to make fair decisions (e.g., drawing by lots, using a random number generator).
7. (+) Analyze decisions and strategies using probability concepts (e.g., product testing, medical testing, pulling a hockey goalie at the end of a game).
S-ID: Interpreting Categorical and Quantitative data
Summarize, represent, and interpret data on two categorical and quantitative variables
5. Summarize categorical data for two categories in two-way frequency tables. Interpret relative frequencies in the context of the data (including joint, marginal, and conditional relative frequencies). Recognize possible associations and trends in the data.
Misconceptions
Student Misconceptions and Common Errors
- Students' intuitions about probability are often incorrect. Students need to be given experiences where they make predictions or estimate probabilities.
- Students often confuse combination and permutations. The fact that we give the students their locker "combination" when, in fact, it is a permutation (the order of the numbers matters) reinforces this misunderstanding.
- Students also often think that there is a "law of small numbers" that certain things are "due" to happen because they have not happened for some time.
- The incorrect use of the word "random." Students use the word to mean "unexpectedly" or "unlikely."
Vignette
In the Classroom
The purpose of this lesson is to have students investigate different counting methods and calculate probabilities. Previously students would have worked with problems similar to the example below to develop techniques for finding the total number of outcomes.
The high school mathematics team is going on a field trip. The choices for lunch are a turkey sandwich, a cheeseburger, or pizza. For dessert the choices are cookies or grapes. How many different meals are possible that consist of one lunch item and one dessert?
Teacher: Several years ago Wendy's started to offer combo choices for their meals. This gives the customer more options for what side they want with their sandwich instead of French fries. Many of the side choices are healthier menu items. Why do you think healthier items have been added to fast food menus?
Student: To attract more people to eat fast food.
Student: Too many people in the United States are overweight.
Student: It might have something to do with the amount of health problems that people are having.
Teacher: Those are some good ideas. It does seem that people are trying to be more health conscious. Some places of work and health insurance companies have been starting to reward people for exercising regularly. Also, in 2004 a documentary called Super-Size Me, in which a man tried to eat McDonalds for breakfast, lunch, and dinner for a month. He became extremely sick and had to stop before a month went by. This documentary also contributed to fast food companies offering healthier choices.
Teacher: We will take a look at combo choices that Wendy's offers to see how many different meals are possible and look at some different probabilities as well. Then we will explore the nutrition information for your favorite combo meal. Here are some choices for Wendy's combo meals that we will consider.
|
Sandwich |
Side |
Drink |
|
1/4 lb. Single |
French Fries |
Coke |
|
1/2 lb. Double |
Garden Side Salad |
Diet Coke |
|
Baconator Single |
Caesar Side Salad |
Sprite |
|
Baconator Double |
Chili |
Dr. Pepper |
|
Bacon Deluxe Single |
Sour Cream and Chives Baked Potato |
Fruit Punch |
|
Bacon Deluxe Double |
|
Root Beer |
|
Spicy Chicken Sandwich |
|
Iced Tea |
|
Homestyle Chicken Fillet |
|
Lemonade |
|
|
|
Water |
Teacher: In your groups talk through the questions on the sheet.
1. How many different combo meals are possible?
2. What is the probability that someone who selected a meal at random would order a homestyle chicken fillet, a Caesar side salad, and a water?
3. If a person selected a combo meal at random what is the probability it would include a bacon deluxe double sandwich?
4. If a person selected a combo meal at random what is the probability it would include a water and a Caesar side salad?
(Students work in groups).
Teacher: Let's hear from groups on how you answered these questions. We will look at number 1 first.
Student: My group started to make a tree diagram and then we realized that it would take a long time to list all of the outcomes so we did a little shorthand to make it easier. We just used S and a number for the different sandwiches. We used abbreviations for the sides; for example, FF was French fries. We knew that there would be 9 choices for drinks, so we just wrote 9 for the different outcomes that would go with each side. Since each side could have nine different drink options we knew that each sandwich had 45 different outcomes or possible combo meals. Then we added up the outcomes or combo meal options and got 360.
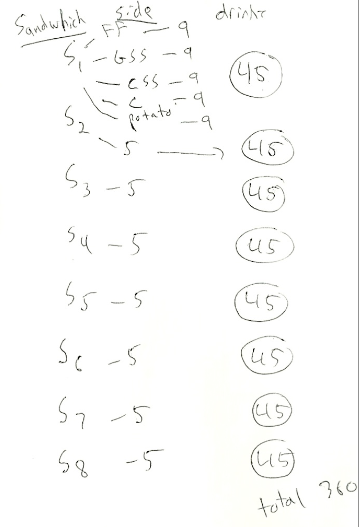
Teacher: Would your answer have been any different if you started with side options, then the drinks, and then the sandwiches at the end since there were 8 sandwich choices.
Student: I don't think so; the tree diagram would look different though.
Student: I can help answer that because our group did something different than a tree diagram. We just took 8 times 5 times 9 to get 360.
Teacher: How does what you did match what is shown in the tree diagram?
Student: Well, there are five sides and each side can be matched with one of the nine drinks, so in a way that is 9 times 5 then. I am not sure about where multiplying by 8 is in the tree diagram.
Student: I think I see it. There are eight 45s circled, so we could add up the 45s to get 360, or just do 8 times 45.
Teacher: So then would it matter what order we did the tree diagram, or multiplied by, to get the total number of outcomes?
Student: No, because if you multiply 8, 5, and 9 in any order it will still be 360.
Teacher: Then for question two, what is the probability that a person who selected a meal at random would order that specific combo meal.
Student: It would be 1 in 360 because the combo meal is one outcome out of a total of 360.
Teacher: Okay, what about question number 3?
Student: Each sandwich has 45 different combo meal possibilities, so chance would be 45 out of 360.
Student: I think it would be 1 out of 8 because there are 8 sandwiches.
Teacher: If we reduced 45 out of 360 what would we get?
Student: Oh, it would be 1 out of 8, or they are both 12.5%.
Teacher: Let's look at question number 4.
Student: It would be 8 out of 360 or about 2.2% of the time.
Teacher: How did you figure this out?
Student: If you have to have a water and Caesar side salad, then the only part you have to look at is the sandwiches since those are the only choices left. There are 8 sandwich choices so 8 different outcomes with a water and Caesar side salad.
Teacher: Good, to close class we will look at a couple of your favorite combo meals to see what the nutritional information is. Then everyone needs to answer the question on the exit slip before the end of class.
Wendy's Menu (Pick the combo meal that you want and then click on the red arrow that says nutrition info).
For an exit slip the students answer the following question before the end of class.
● In the example below, which restaurant's combo meals would have more possible outcomes?
Wendy's: 12 choices for sandwiches, 8 choices for sides, and 10 choices for drinks.
Panera: 10 choices for sandwiches, 4 choices for sides, and 15 choices for drinks.
Resources
Teacher Notes
- Teachers need to be clear on the differences between a decision and an outcome.
- Teachers need to use terminology correctly and correct students when they misuse terms.
- Teachers can point out common misuses of the terminology in print and media.
- Teachers may want to point out that computer-based number generators are "pseudo-random" and not truly random. That is they act random, but are not based on random phenomena.
- Teachers should work with science teachers and incorporate topics and problems that students are seeing in their science courses.
Lesson was adapted from "Activities: Explorations with Chance," Mathematics Teacher (April, 1992). In this lesson, students analyze the fairness of certain games by examining the probabilities of the outcomes. The explorations provide opportunities to predict results, play the games, and calculate probabilities. Students should have had prior experiences with simple probability investigations, including flipping coins, drawing items from a set, and making tree diagrams. They should understand that the probability of an event is the ratio of the number of successful outcomes to the number of possible outcomes.
Stick or Switch? Lesson was adapted from an article by J.M. Shaughnessy & T. Dick, Mathematics Teacher (April 1991). This lesson plan presents a classic game-show scenario. A student picks one of three doors in the hopes of winning the prize. The host, who knows the door behind which the prize is hidden, opens one of the two remaining doors. When no prize is revealed, the host asks if the student wishes to "stick or switch." Which choice gives you the best chance to win? The approach in this activity runs from guesses to experiments to computer simulations to theoretical models.
Web Links for Data Analysis and Probability
Additional Instructional Resources
- Journal of Statistics Education
This international journal is on the teaching and learning of statistics. - The Exploring Data-Math Forum
This site provides standards, data sets, lessons and websites at the K-4, 5-8, and 9-12 levels. - The Texas Instruments Classroom Activities Exchange
The site can be used to supplement lessons on the concepts in Gr. 9-12 Data Analysis and Probability.
addition principle: If two or more events have no common outcomes, than the total number of outcomes can be calculated by adding up the possible outcomes for each event.
multiplication principle: If you can do one task in "a" number of ways and a second task in "b" number of ways, then both tasks can be done in a x b number of ways.
sample space: In a probability model for a random process, a list of the individual outcomes that are to be considered.
tree diagram: A visual to show all possible outcomes of an event.
Professional Learning Communities
Reflection - Critical Questions regarding the teaching and learning of these benchmarks:
- How can you better plan your lessons in the future so students have experiences with making predictions or estimating probabilities with relevant real world situations?
- How well structured were the activities for students to explain their reasoning or intuitions and then confront or recognize any misconceptions that they had?
- How well can students explain where they will need knowledge of probability in their lives?
- Were students able to explain or demonstrate their knowledge in different representations (language, real world situations, pictorial, symbols, and manipulatives)? How can you facilitate students' translations between representations for more conceptual knowledge?
Materials - suggested articles and books
American Statistical Association. (2007). Publications for assessment and instruction in statistics education.
Haberman, M. (1991). The pedagogy of poverty versus good teaching. Phi Delta Kapan, December, 291-294.
Peck, R., Starnes, D., Kranendank, H., & Morita, J. (2009). Making sense of statistical studies: Teacher's module. Alexandria, VA: American Statistical Association.
This book consists of 15 hands-on investigations that provide students with valuable experience in designing and analyzing statistical studies. It is written for an upper middle-school or high-school audience. Each investigation includes a descriptive overview, prior knowledge that students need, learning objectives, teaching tips, references, possible extensions, and suggested answers.
This is the K-12 portion of the American Statistical Association (ASA) website. They have workshops and online resources for teachers, useful websites, student competitions, and a list of publications in statistics education.
Rosenstien, J., Caldwell, J., & Crown, W. (1996). New Jersey mathematics curriculum framework. Trenton, NJ: New Jersey State Department of Education.
SciMath Minnesota. (1997). Minnesota k-12 mathematics framework. St. Paul, MN: SciMath.
Yates, D. S., Starnes, D S., & Moore, D. S. (2005) Statistics through application. New York: W.H Freeman
Assessment
- (DOK level 2: Basic Reasoning) Tara plays a game using 2 bags of game pieces. One bag has 6 blue game pieces and 6 red game pieces. The other bag has ten game pieces numbered 1 through 10. On her turn, Tara must draw one game piece from each bag. What is the probability that she draws a red game piece and an even-numbered game piece?
A) ½ (B) ¼ ( C) 1/30 (D) 1/60 (Colorado Department of Education, 2001 CSAP grade 10 released items, p.14. Retrieved from: http://www.cde.state.co.us/cdeassess/documents/csap/2001/RE01ma10.pdf)
- (DOK level 2: Basic Reasoning) Julio's music appreciation class is studying examples of classical music used in films. Each student is randomly assigned to report on two of the selections listed in the table.

FCAT 2006 Mathematics released test, Florida Department of Education. Retrieved from: http://fcat.fldoe.org/pdf/releasepdf/06/FL06_Rel_G10M_TB_Cwf001.pdf p. 27).
- (DOK level 1: Recall) A fish tank at a pet store has 3 red fish, 6 blue fish, 7 yellow fish, and 4 orange fish. If one fish is chosen at random from the tank, what is the probability that the fish will be blue or yellow?
Maryland State Department of Education, 2009, Algebra/data analysis public release, p.34. Retrieved from: http://mdk12.org/assessments/high_school/look_like/2009/algebra/hsaAlgebra.pdf)
Differentiation
- Strategies: Real world problem solving, multiple entry points, vary teaching methods, group work, teach problem solving strategies.
- Challenges: motivation, slower processing, reading and writing ability, organization, and behavior issues and coping strategies.
English Language Learners
Teachers must be explicit in how they talk of vocabulary terms and use vocabulary in context. Teachers should use vocabulary terms often so that students will become familiar hearing them in context. Students should also be allowed to practice the use of vocabulary in small groups.
- Strategies: modeling vocabulary, using manipulatives, speaking slowly, using visuals, using a variety of assessments, assigning group work, verbalizing reasoning, understanding context or concept, making personal dictionaries.
- Challenges: Vocabulary and Reading ability, standardized tests, how to approach problem solving, and cultural differences.
Minnesota Council for the Gifted and Talented
- Strategies: Tiered objectives, open-ended problem solving, grouping (heterogeneous and homogeneous), curriculum compacting, and independent investigations.
- Challenges: Motivation, acceleration and attitude associated with this for students, maturity, isolation and social issues, and not wanting to be moved outside of age group.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are... |
Teachers are... |
|
conducting probability experiments. |
facilitating student learning by structuring activities for students to work in groups. |
|
creating hypotheses. |
leading discourse that allows students to communicate their ideas. |
|
investigating relevant real world problems. |
presenting engaging problems that allow student understanding to build on others' ideas. |
|
providing justification for their ideas. |
engaging students by using technology. |
|
refining their strategies and ideas. |
instructing to allow students to develop ideas and construct their knowledge. |
|
thinking critically about events and probabilities. |
|
"The best way to approach this content is with open-ended investigations that allow the students to arrive at their own conclusions through experimentation and discussion." (New Jersey Mathematics Curriculum Framework, 1996, p. 371)
Parent Resources
- Lohr, Steve. (2009). For Today's Graduate, Just one word: Statistics. New York Times. This is an article about the growing variety of jobs in statistics that are available due to the advancements in technology.
- National Library of Virtual Manipulatives. This website has a variety of applets and activities for students to explore patterns and investigate probability.
- High School Statistics Resources for Teachers, Parents, and Students.This website has summary information of other websites that can be helpful for further information, practice, and exploration for students.
- This website has collections of articles regarding statistics and probability. It contains numerous current events that relate to statistics.
