9.3.4B Coordinate Geometry, Circles & Transformations
Solve real-world and mathematical geometric problems using algebraic methods.
Use coordinate geometry to represent and analyze line segments and polygons, including determining lengths, midpoints and slopes of line segments.
Know the equation for the graph of a circle with radius r and center (h, k), (x - h)2 + (y - k)2 = r2, and justify this equation using the Pythagorean Theorem and properties of translations.
Use numeric, graphic and symbolic representations of transformations in two dimensions, such as reflections, translations, scale changes and rotations about the origin by multiples of 90˚, to solve problems involving figures on a coordinate grid.
For example: If the point (3,-2) is rotated 90˚ counterclockwise about the origin, it becomes the point (2,3).
Overview
Standard 9.3.4 Essential Understandings
Students focusing on geometry have typically already learned and used a significant amount of algebra in their mathematics course work. This might mean they have completed at least one separate course in algebra or have studied algebra as part of an integrated approach to mathematics. Either way, they must be able to recognize the close, integral relationship between algebra and geometry and be able to use this interconnectedness to solve mathematical problems. Activities in this standard will help students do this by showing them places in their course work and also in real life where geometry and algebra are used together in order to solve problems.
In this standard, students will connect algebra and geometry in a number of ways. They will calculate distances and angle measures using trigonometric ratios. They will look at slope of a line, midpoint of a segment and length of a segment using formulas derived from coordinate geometry. They will calculate geometric transformations through the use of the Cartesian plane. In addition, they will graph diameter and circumference of round objects, in order to see a visual interpretation of the number pi.
All Standard Benchmarks
9.3.4.1
Understand how the properties of similar right triangles allow the trigonometric ratios to be defined, and determine the sine, cosine and tangent of an acute angle in a right triangle.
9.3.4.2
Apply the trigonometric ratios sine, cosine and tangent to solve problems, such as determining lengths and areas in right triangles and in figures that can be decomposed into right triangles. Know how to use calculators, tables or other technology to evaluate trigonometric ratios.
9.3.4.3
Use calculators, tables or other technologies in connection with the trigonometric ratios to find angle measures in right triangles in various contexts.
9.3.4.4
Use coordinate geometry to represent and analyze line segments and polygons, including determining lengths, midpoints and slopes of line segments.
9.3.4.5
Know the equation for the graph of a circle with radius r and center (h, k), (x - h)2 + (y - k)2 = r2, and justify this equation using the Pythagorean Theorem and properties of translations.
9.3.4.6
Use numeric, graphic and symbolic representations of transformations in two dimensions, such as reflections, translations, scale changes and rotations about the origin by multiples of 90˚, to solve problems involving figures on a coordinate grid.
9.3.4.7
Use algebra to solve geometric problems unrelated to coordinate geometry, such as solving for an unknown length in a figure involving similar triangles, or using the Pythagorean Theorem to obtain a quadratic equation for a length in a geometric figure.
9.3.4 Benchmark Group B - Coordinate Geometry, Circles, and Transformations
9.3.4.4
Use coordinate geometry to represent and analyze line segments and polygons, including determining lengths, midpoints and slopes of line segments.
9.3.4.5
Know the equation for the graph of a circle with radius r and center (h, k), (x - h)2 + (y - k)2 = r2, and justify this equation using the Pythagorean Theorem and properties of translations.
9.3.4.6
Use numeric, graphic and symbolic representations of transformations in two dimensions, such as reflections, translations, scale changes and rotations about the origin by multiples of 90˚, to solve problems involving figures on a coordinate grid.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Calculate slope of a line or segment;
- Calculate the distance between two points on a coordinate plane;
- Calculate the midpoint of a segment, given the coordinates of the endpoints;
- List the center and radius of a circle, given its equation;
- Write the equation of a circle, given its center and radius (or diameter);
- Calculate the coordinates of a point after an isometry (reflection over an axis, rotation of a multiple of 90 degrees about the origin, translation).
Work from previous grades that supports this new learning includes:
- Be familiar with the Cartesian coordinate system;
- Have done prior work with transformations, especially isometries (reflections, rotations, translations, glide reflections);
- Have knowledge of circles and related terms (circumference, radius, diameter).
NCTM Standards
Geometry
Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships:
- Analyze properties and determine attributes of two- and three-dimensional objects;
- Use trigonometric relationships to determine lengths and angle measures.
Specifylocations and describe spatial relationships using coordinate geometry and other representational systems:
- Use Cartesian coordinates and other coordinate systems, such as navigational, polar, or spherical systems, to analyze geometric situations;
- Investigate conjectures and solve problems involving two- and three-dimensional objects represented with Cartesian coordinates.
Apply transformations and use symmetry to analyze mathematical situations:
- Understand and represent translations, reflections, rotations, and dilations of objects in the plane by using sketches, coordinates, vectors, function notation, and matrices;
- Use various representations to help understand the effects of simple transformations and their compositions.
Common Core State Standards (CCSS)
HS.G-SRT (Similarity, Right Triangles, & Trigonometry) Define trigonometric ratios and solve problems involving right triangles.
- HS.G-SRT.8. Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
HS.G-SRT (Similarity, Right Triangles, & Trigonometry) Apply trigonometry to general triangles.
- HS.G-SRT.9. Explain and use the relationship between the sine and cosine of complementary angles.
- HS.G-SRT.10. Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
HS.G-GPE (Expressing Geometric Properties with Equations) Translate between the geometric description and the equation for a conic section.
- HS.G-GPE.1. Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation.
HS.G-GPE (Expressing Geometric Properties with Equations) Use coordinates to prove simple geometric theorems algebraically.
- HS.G-GPE.4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, 2).
- HS.G-GPE.7. Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula.
HS.G-CO (Congruence) Experiment with transformations in the plane.
- HS.G-CO.2. Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch).
- HS.G-CO.3. Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself.
- HS.G-CO.4. Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.
- HS.G-CO.5. Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.
HS.A-CED (Creating Equations) Create equations that describe numbers or relationships.
- HS.A-CED.1. Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear and quadratic functions, and simple rational and exponential functions.
Misconceptions
Student Misconceptions and Common Errors
- Students sometimes confuse clockwise rotations with counterclockwise rotations.
- Students sometimes confuse a rotation of positive degree measure, which rotates a figure counterclockwise, with a rotation of negative degree measure, which rotates a figure clockwise.
- Students often mistake the formula for slope with the formula for midpoint and/or the Distance Formula.
Vignette
In the Classroom
Vignette.1
The following incorporates the use of an interactive geometry program. It might be a commercially-available software package, or a program available for free on the Internet, or another resource; most will suffice for this activity. The first part is an activity done in "Teacher demo" mode, with the teacher and students in the classroom, in a whole-group discussion format. The teacher is manipulating the geometry program.
The teacher puts a vertical segment on the board, like this:
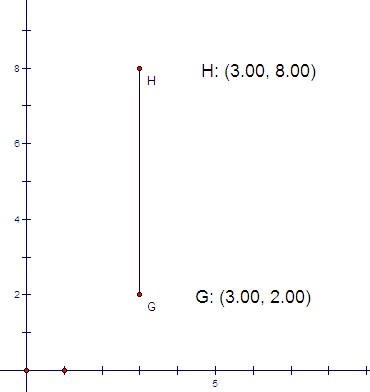
Teacher: What would you do to find the coordinates of the midpoint of this segment?
Student 1: Wouldn't it be just halfway between 2 and 8?
Teacher: What do you mean?
Student 1: We know that the two endpoints have the same x-coordinate, so we could just take the average of their y-coordinates.
Teacher: Then, what would be the coordinates of the midpoint?
Student 1: The midpoint would be at (3, 5).
Teacher: How about the coordinates of the midpoint of this segment?
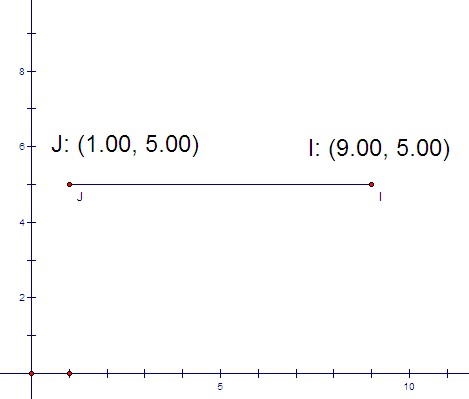
Student 2: Couldn't we just do the same thing, except with the x-coordinates instead this time?
Teacher: OK, if you do that, what would be the coordinates of the midpoint?
Student 2: (5, 5)
Teacher: Great. What if the segment is neither vertical nor horizontal, like this one?
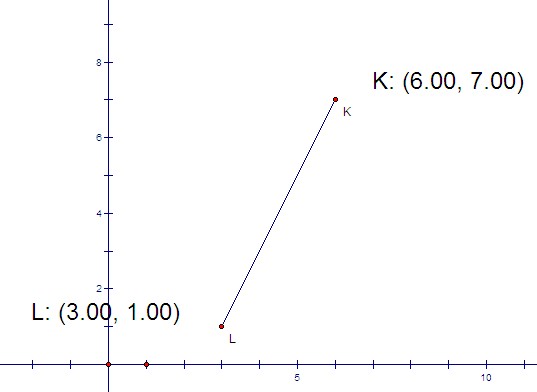
Student 3: Well, if we took the average of the y-coordinates the first time, and we took the average of the x-coordinates the second time, couldn't we just combine those, and take the average of both coordinates this time?
Teacher: Very good. If you do that, then what would you get for the coordinates of the midpoint of this segment?
Student 3: (4.5, 4)
Teacher: Could you generalize a formula to find the midpoint of a segment if you're given the coordinates of the endpoints?
Student 4: I could try.
Teacher: OK, if you have a point T(x1, y1) and a point E(x2, y2), then what would you do to get the coordinates of the midpoint?
Student 4: $\left (\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right )$
Teacher: Excellent. Let's look at a different aspect of this segment. What would you do if you wanted to find the length of segment LK above?
Student 5: If we had a right triangle, we could use the Pythagorean Theorem.
Teacher: In what way?
Student 5: Well, we could square the one leg, then square the other leg, and add those together, and take the square root, and that would give us the length.
Teacher: That would be great, if we had a right triangle, but we don't.
Student 5: We could make one, by dropping a vertical segment from K and a horizontal segment from L. The point where they meet, M, will be the vertex of the right angle, so we'll have a right triangle. It looks like this:
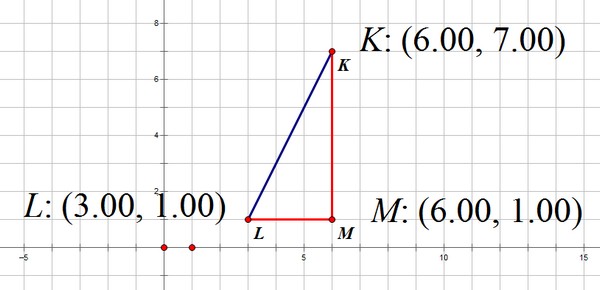
Teacher: How can you use that to calculate the length of segment KL?
Student 5: We know the length of the horizontal leg - that's 3 units. We know the length of the vertical leg - that's 6 units. If we square 3, we get 9, and if we square 6, we get 36. If we add 9 and 36, we get 45, so the length is $\sqrt{45}$ .
Teacher: Good job. Is there a way we can generalize a formula, similar to what you did for the midpoint of a segment? Again, let's say you have a point T(x1, y1) and a point E(x2, y2). What would you do to calculate the length of segment TE?
Student 5: I think it would look like this:
$\sqrt{\left ( x_{2}-x_{1} \right )^{2}+\left ( y_{2}-y_{1} \right )^{2}}$
Teacher: OK, now we've gone through two of the "Big Three" ideas in regard to segments. We've been able to generate formulas for the midpoint of a segment and the length of a segment, given the coordinates of the two endpoints. Now let's look at the third part - the slope of the line or, in this case, the segment.
Student 6: I think I remember that in algebra class, slope was described as the amount of slant or tilt of a line.
Student 7: My teacher said it was the rate of change of a line.
Student 8: Mine said it was "rise over run," whatever that means.
Student 9: I remember that if a line went up from left to right, it had positive slope, and if it went down from left to right, it had negative slope.
Student 6: Who's right?
Teacher: In a way, you all are right. We often describe slope as a way to show the rate of change of a line. Slope is the ratio of the vertical change of the line divided by the horizontal change of the line. Let's look at the example we used for the first two topics, and see if we can figure out the slope of that segment.
Student 7: You said that slope had to do with a line, and now we're trying to figure out the slope of a segment? Why?
Teacher: Good question. Remember that a segment is a part of a line. That line would continue forever on either side of the endpoints of the segment, so when we calculate the slope of the segment, we're also calculating the slope of the line that contains the segment.
Student 7: I understand.
Teacher: Great. Let's look at the segment we used earlier:
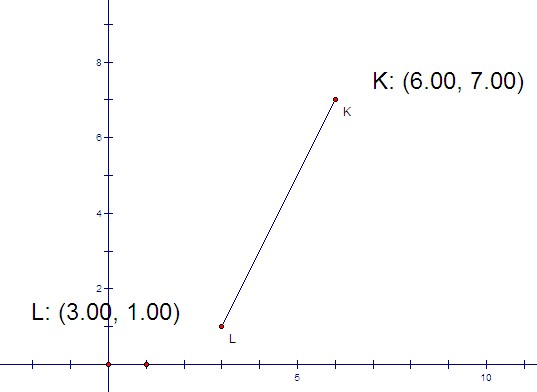
Teacher: How could you calculate the vertical change?
Student 9: You could figure out the distance between the y-coordinates. In this case, it's the difference between 7 and 1, or 6.
Teacher: Yes. How could you calculate the vertical change?
Student 9: You could figure out the distance between the x-coordinates. In this case, it's the difference between 6 and 3, or 3.
Teacher: Great. So, what would you do to find the ratio of the vertical change and the horizontal change?
Student 9: Just divide 6 by 3, and get a ratio of 2:1.
Teacher: What do you suppose that ratio means for this particular segment?
Student 8: That for every two units the segment changes vertically, it changes one unit horizontally.
Teacher: Excellent. Now, let's look at slope the same way we looked at the length of a segment and the midpoint of a segment. Again, let's say you have a point T(x1, y1) and a point E(x2, y2). What would you do to calculate the slope of segment TE?
Student 5: I think it would look like this:
$\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
Teacher: That looks great.
Vignette.2
The following activity assumes access to a computer lab, with a pair of students working on each computer. If no computer lab is available, then this activity is easily done in "demonstration" mode.
Interactive Geometry lab
In this lab, you will be working with circles and polygons. The purpose of the first part of this lab is to determine how the equation of a circle relates to some of the features of the circle. The purpose of the second part of the lab is to have you learn about rotations about the origin in a coordinate plane.
1. Use the circle tool to place a circle on your computer screen. For now, keep the circle in the upper-right part of the screen.
With the circle selected, in the menu bar, click "Measure" and measure the equation of the circle. You'll notice that in addition to the equation of the circle now on your screen, you have a coordinate grid. The circle's equation will be put on your screen in the format (x - h)2 + (y - k)2 = r2. We will explore the importance of "h," "k," and "r" as they relate to the circle.
2. Select the center of the circle and move that point. What do you notice about h, k and r?
3. Select just the circle itself, and move it around on your screen. What do you notice about h, k and r?
4. When you put the circle on your screen, you clicked on the center and dragged out to a point on the circle. Select just the point on the circle that was created when you did this, and move it around on your screen. What do you notice about h, k and r?
5. How do h, k and r seem to relate to the equation of the circle? Stop here and discuss this with your partner and one other pair of students. Write an answer in the space below.
6. Select the center of the circle. Under the "Measure" menu, measure the center's coordinates. Move the circle around on the screen. What do you notice about the equation of the circle and the coordinates of the center?
7. Select just the circle. Under the "Measure" menu, measure the circle's radius. Move the circle around on the screen. What do you notice about the equation of the circle and the radius?
8. Describe how h, k and r relate to the equation of the circle. Complete the following:
Given the equation of a circle, (x - h)2 + (y - k)2 = r2,
h is
k is
and r is
9. Put a new sketch on your screen. Draw a polygon and measure the coordinates of the vertices. Mark the origin (that is, the point (0, 0)) as the center of rotation, and select the entire polygon. Rotate the polygon 90 degrees. Notice that this rotation moves the figure counterclockwise. Select a vertex and move it around, noting the coordinates of the preimage and its corresponding image. What do you notice?
10. A certain point has coordinates (x, y), If that point is rotated 90 degrees about the origin, then the coordinates of the image are:
_____________________.
11. Use a new polygon and perform the same procedure as above, but rotate the polygon 180 degrees.
12. A certain point has coordinates (x, y), If that point is rotated 180 degrees about the origin, then the coordinates of the image are:
_____________________.
This particular transformation has the same effect as another transformation that you've studied. Which transformation is it? Describe it in detail.
__________________________________________________________________
__________________________________________________________________
13. Use a new polygon and perform the same procedure as above, but rotate the polygon 270 degrees.
14. A certain point has coordinates (x, y), If that point is rotated 270 degrees about the origin, then the coordinates of the image are:
____________________.
The following might be an example of student work on the lab:
Interactive Geometry lab
In this lab, you will be working with circles and polygons. The purpose of the first part of this lab is to determine how the equation of a circle relates to some of the features of the circle. The purpose of the second part of the lab is to have you learn about rotations about the origin in a coordinate plane.
1. Use the circle tool to place a circle on your computer screen. For now, keep the circle in the upper-right part of the screen.
With the circle selected, in the menu bar, click "Measure" and measure the equation of the circle. You'll notice that in addition to the equation of the circle now on your screen, you have a coordinate grid. The circle's equation will be put on your screen in the format (x - h)2 + (y - k)2 = r2. We will explore the importance of "h," "k," and "r" as they relate to the circle.
(The student's screen might look like the following:)
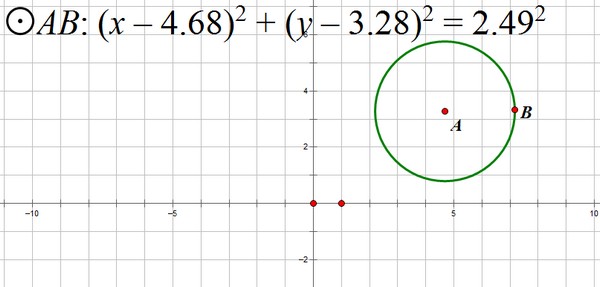
2. Select the center of the circle and move that point. What do you notice about h, k and r?
It looks like h, k and r all change as I move the center around the screen.
3. Select just the circle itself, and move it around on your screen. What do you notice about h, k and r?
It appears that h and k change as I move the circle, but r stays the same.
4. When you put the circle on your screen, you clicked on the center and dragged out to a point on the circle. Select just the point on the circle that was created when you did this, and move it around on your screen. What do you notice about h, k and r?
It appears that h and k stay the same as I move the point, but r changes.
5. How do h, k and r seem to relate to the equation of the circle? Stop here and discuss this with your partner and one other pair of students. Write an answer in the space below.
I think h and k have something to do with the center of the circle, and r has something to do with the radius.
6. Select the center of the circle. Under the "Measure" menu, measure the center's coordinates. Move the circle around on the screen. What do you notice about the equation of the circle and the coordinates of the center?
The coordinates of the center are in the equation.
7. Select just the circle. Under the "Measure" menu, measure the circle's radius. Move the circle around on the screen. What do you notice about the equation of the circle and the radius?
The radius is in the equation. (The student's screen might look like the following:)
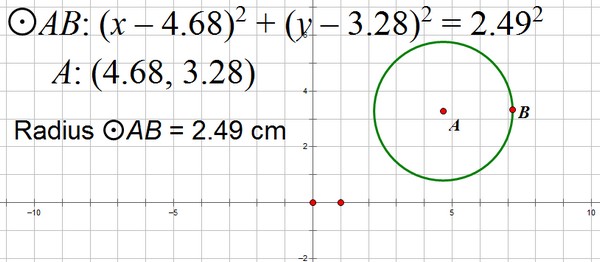
8. Describe how h, k and r relate to the equation of the circle. Complete the following:
Given the equation of a circle, (x - h)2 + (y - k)2 = r2,
h is the x-coordinate of the center of the circle
k is the y-coordinate of the center of the circle
and r is the radius of the circle.
9. Put a new sketch on your screen. Draw a polygon and measure the coordinates of the vertices. Mark the origin (that is, the point (0, 0)) as the center of rotation, and select the entire polygon. Rotate the polygon 90 degrees. Notice that this rotation moves the figure counterclockwise. Select a vertex and move it around, noting the coordinates of the preimage and its corresponding image. What do you notice?
They have the same numbers, but they're switched, and one of them is the opposite.
10. A certain point has coordinates (x, y), If that point is rotated 90 degrees about the origin, then the coordinates of the image are:
_______ (-y, x) ______________.
11. Use a new polygon and perform the same procedure as above, but rotate the polygon 180 degrees.
12. A certain point has coordinates (x, y), If that point is rotated 180 degrees about the origin, then the coordinates of the image are:
________ (-x, -y) _____________.
This particular transformation has the same effect as another transformation that you've studied. Which transformation is it? Describe it in detail.
It is the same as when we reflected the figure over the x-axis, and then reflected that image over the y-axis (or reflected over the y-axis first, and then reflected that image over the x-axis).
13. Use a new polygon and perform the same procedure as above, but rotate the polygon 270 degrees.
14. A certain point has coordinates (x, y), If that point is rotated 270 degrees about the origin, then the coordinates of the image are:
_________ (y, -x) ____________.
Resources
Teacher Notes
- Be aware of student misconceptions, especially in terms of mixing up the formulas for midpoint, slope and distance between two points.
- Be conscious that a mistake in the Vignette activities might be due to a conceptual issue with the mathematics, but if your students are in a computer lab situation, any mistakes could also be a problem working the particular software involved.
- Be sure to emphasize the idea that a rotation of positive degree measure is a counterclockwise rotation, and a rotation of negative degree measure is a clockwise rotation.
- Be mindful of student errors in applying formulas, especially the "big three" formulas for slope, midpoint and distance between points.
Growth Rate
Given growth charts for the heights of girls and boys, students will use slope to approximate rates of change in the height of boys and girls at different ages. Students will use these approximations to plot graphs of the rate of change of height vs. age for boys and girls.
Additional Instructional Resources
National Council of Teachers of Mathematics (NCTM). (2010). Focus in High School Mathematics: Reasoning and Sense Making in Geometry. Reston, VA: National Council of Teachers of Mathematics.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What other instructional strategies can be used to engage students' study of angles associated with parallel and perpendicular lines?
- How can manipulatives be used to help students visualize these abstract concepts?
- How can the instruction be scaffolded for students?
- What additional scaffolding is needed to provide ELL students?
- Do the tasks that have been designed connect to underlying concepts or focus on memorization?
- How can it be determined if students have reached this learning goal?
- How can the lesson be differentiated?
Assessment
1. Use a segment with endpoints M(1, 8) and K(4, 2). Calculate the following:
a. the coordinates of the midpoint of segment MK
b. the length of segment MK
c. the slope of segment MK
d. the coordinates of M' and K' if segment MK is rotated 90 degrees counterclockwise about the origin
e. the coordinates of M'' and K'' if the original segment MK is rotated 180 degrees counterclockwise about the origin
f. the coordinates of M''' and K''' if the original segment MK is rotated 270 degrees counterclockwise about the origin
g. the equation of the circle with center M and having K as a point on the circle
Answers:
1. DOK Level: 2
a. (2.5, 5)
b. $\sqrt{45}$
c. -2, or -2/1
d. M'(-8, 1) K'(-2, 4)
e. M''(-1, -8) K''(-4, -2)
f. M'''(8, -1) K'''(2, -4)
g. (x - 1)2 + (y - 8)2 = 45
Differentiation
- Break up the Vignette.2 activity into two sections, done on two days. The first day, do the part with the circles, and the second day, do the part with the rotations. Be sure to debrief about the lab each day.
- When splitting the class into pairs for the Vignette.2 lab work, be sure that an ELL student is paired with a non-ELL student. They should both be able to manipulate the keyboard/mouse; in this regard, they will both be able to clearly see the changes in the figures.
- Add other transformations to the Vignette.2 situation, such as a dilation or a glide reflection of a triangle or other polygon.
- Extend these ideas to three-dimensional space, developing the Midpoint Formula and Distance Formula for segments in three dimensions.
- Computer Animation - Transformations
In this lesson, students transform images through rotation, reflection, dilation and translation using matrix multiplication. After digitizing images by representing the images as matrices, they multiply image matrices by various transformation matrices, producing transformed images.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) | Teachers are: (descriptive list) |
working in pairs in a computer lab setting. | splitting the students into pairs for the computer lab Vignette activity. |
discussing the mathematics behind the lab work. | walking around the lab, observing and giving help where needed. |
making conjectures about the figures, and checking their conjectures. |
|
Parent Resources
- Sophia geometry lessons
This social learning community website includes lessons on multiple topics. Most of these lessons were developed by teachers and reviewed.
- Khan Academy geometry lessons
This website offers a library of videos and practice exercises on multiple topics.
- Teacher Tube, YouTube
These websites include multiple uploaded lessons on most school topics.
- Mathematics textbooks
Many textbook publishers have websites with additional resources and tutorials. Check your child's textbook for a weblink.
