9.2.4B Represent & Solve Systems of Linear Inequalities
Represent relationships in various contexts using systems of linear inequalities; solve them graphically. Indicate which parts of the boundary are included in and excluded from the solution set using solid and dotted lines.
Solve linear programming problems in two variables using graphical methods.
Represent relationships in various contexts using absolute value inequalities in two variables; solve them graphically.
For example: If a pipe is to be cut to a length of 5 meters accurate to within a tenth of its diameter, the relationship between the length x of the pipe and its diameter y satisfies the inequality | x - 5| ≤ 0.1y.
Overview
Standard 9.2.4 Essential Understandings
In this standard, students learn to model real-world mathematical situations using linear, quadratic, exponential and nth root functions. In order to do so, they need to understand the characteristics of each type of function: linear functions have a constant rate of change; quadratic functions have a linear rate of change (the rate of change of the rate of change, or the 2nd difference, is constant); and exponential functions have a rate of change that is proportional to the value of the function (the output is multiplied by a constant factor).
Students need to be able to choose from a variety of methods to solve these functions, whether symbolically or graphically. Once solutions are found, students need to be able to determine the reasonableness of an answer given the real-world context for the function - a particular solution may not be applicable in the original context.
Students need to understand the real number system, including the subsets of natural and whole numbers, integers, rational and irrational numbers, and that many of these numbers were invented to solve equations. They need to know how the real number system fits into the non-real complex number system, and how operations in the non-real complex number system correspond to those of the real number system. Students need to understand how a solution in the non-real complex number system is graphed, and what that solution means in terms of a given context for a quadratic equation.
Students need to be comfortable in using a graphing calculator or other graphing utilities to find solutions and describe characteristics of linear, quadratic and exponential functions. They should know how to use the table and graphing features to check solutions for these functions.
All Standard Benchmarks
9.2.4.1
Represent relationships in various contexts using quadratic equations and inequalities. Solve quadratic equations and inequalities by appropriate methods including factoring, completing the square, graphing and the quadratic formula. Find non-real complex roots when they exist. Recognize that a particular solution may not be applicable in the original context. Know how to use calculators, graphing utilities or other technology to solve quadratic equations and inequalities.
Example: A diver jumps from a 20 meter platform with an upward velocity of 3 meters per second. In finding the time at which the diver hits the surface of the water, the resulting quadratic equation has a positive and a negative solution. The negative solution should be discarded because of the context.
9.2.4.2
Represent relationships in various contexts using equations involving exponential functions; solve these equations graphically or numerically. Know how to use calculators, graphing utilities or other technology to solve these equations.
9.2.4.3
Recognize that to solve certain equations, number systems need to be extended from whole numbers to integers, from integers to rational numbers, from rational numbers to real numbers, and from real numbers to complex numbers. In particular, non-real complex numbers are needed to solve some quadratic equations with real coefficients.
9.2.4.4
Represent relationships in various contexts using systems of linear inequalities; solve them graphically. Indicate which parts of the boundary are included in and excluded from the solution set using solid and dotted lines.
9.2.4.5
Solve linear programming problems in two variables using graphical methods.
9.2.4.6
Represent relationships in various contexts using absolute value inequalities in two variables; solve them graphically.
Example: If a pipe is to be cut to a length of 5 meters, accurate to within a tenth of its diameter, the relationship between the length x of the pipe and its diameter y satisfies the inequality | x - 5| ≤ 0.1y.
9.2.4.7
Solve equations that contain radical expressions. Recognize that extraneous solutions may arise when using symbolic methods.
Example: The equation ![]() may be solved by squaring both sides to obtain x - 9 = 81x, which has the solution
may be solved by squaring both sides to obtain x - 9 = 81x, which has the solution ![]() . However, this is not a solution of the original equation, so it is an extraneous solution that should be discarded. The original equation has no solution in this case.
. However, this is not a solution of the original equation, so it is an extraneous solution that should be discarded. The original equation has no solution in this case.
Another example: Solve ![]() .
.
9.2.4.8
Assess the reasonableness of a solution in its given context and compare the solution to appropriate graphical or numerical estimates; interpret a solution in the original context.
9.2.4 Algebra Benchmark Group B Represent and Solve Systems of Linear Inequalities
9.2.4.4
Represent relationships in various contexts using systems of linear inequalities; solve them graphically. Indicate which parts of the boundary are included in and excluded from the solution set using solid and dotted lines.
9.2.4.5
Solve linear programming problems in two variables using graphical methods.
9.2.4.6
Represent relationships in various contexts using absolute value inequalities in two variables; solve them graphically.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Set up a system of linear equations or inequalities to represent given real-world contexts;
- Solve systems of linear inequalities by graphing, using the inequalities to determine whether the boundaries should be included in the solution set (solid lines to represent <, =, or >) or should not be included in the solution set (dotted lines to represent < or >);
- Solve linear programming problems with two variables using graphing to determine a feasible region and test intersection points using a constraint function;
- Model relationships involving absolute value functions and inequalities.
Work from previous grades that supports this new learning includes:
- Use linear functions to represent relationships with a constant rate of change;
- Identify graphical properties of linear functions including slopes and intercepts;
- Use linear inequalities to represent relationships in various contexts, and should be able to solve linear inequalities;
- Represent relationships in various contexts using systems of linear equations. They should be able to solve systems of linear equations in two variables symbolically, graphically and numerically;
- Understand that a system of linear equations may have no solution, one solution, or an infinite number of solutions. They should be able to relate the number of solutions to pairs of lines that are intersecting, parallel, or identical. They should be able to check whether a pair of numbers representing a point satisfies a system of two linear equations in two unknowns by substituting the numbers into both equations.
NCTM Standards
Understand patterns, relations, and functions:
- Generalize patterns using explicitly defined and recursively defined functions;
- Understand relations and functions and select, convert flexibly among, and use various representations for them;
- Analyze functions of one variable by investigating rates of change, intercepts, zeros, asymptotes, and local and global behavior;
- Understand and perform transformations, such as arithmetically combining, composing, and inverting commonly used functions, using technology to perform such operations on more-complicated symbolic expressions;
- Understand and compare the properties of classes of functions, including exponential, polynomial, rational, logarithmic, and periodic functions;
- Interpret representations of functions of two variables.
Represent and analyze mathematical situations and structures using algebraic symbols:
- Understand the meaning of equivalent forms of expressions, equations, inequalities, and relations;
- Write equivalent forms of equations, inequalities, and systems of equations and solve them with fluency - mentally or with paper and pencil in simple cases and using technology in all cases;
- Use symbolic algebra to represent and explain mathematical relationships;
- Use a variety of symbolic representations, including recursive and parametric equations, for functions and relations;
- Judge the meaning, utility, and reasonableness of the results of symbol manipulations, including those carried out by technology.
Use mathematical models to represent and understand quantitative relationships:
- Identify essential quantitative relationships in a situation and determine the class or classes of functions that might model the relationships;
- Use symbolic expressions, including iterative and recursive forms, to represent relationships arising from various contexts;
- Draw reasonable conclusions about a situation being modeled.
Analyze change in various context:
- Approximate and interpret rates of change from graphical and numerical data.
Common Core State Standards (CCSM)
A-SSE (Seeing Structure In Expressions) Write expressions in equivalent forms to solve problems.
- A-SSE.3.Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
A-SSE.3.a. Factor a quadratic expression to reveal the zeros of the function it defines.
A-SSE.3.b. Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.
A-SSE.3.c. Use the properties of exponents to transform expressions for exponential functions. For example, the expression 1.15t can be rewritten as (1.151/12)12t ≈ 1.01212t to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
- A-SSE.4. Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems. For example, calculate mortgage payments.
A-CED (Creating Equations) Create equations that describe numbers or relationships.
- A-CED.1.Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear and quadratic functions, and simple rational and exponential functions.
- A-CED.2.Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales
- A-CED.3.Represent constraints by equations or inequalities, and by systems of equations and/or inequalities, and interpret solutions as viable or nonviable options in a modeling context.For example, represent inequalities describing nutritional and cost constraints on combinations of different foods.
A-REI (Reasoning with Equations and Inequalities) Understand solving equations as a process of reasoning and explain the reasoning.
- A-REI.1.Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, starting from the assumption that the original equation has a solution. Construct a viable argument to justify a solution method.
- A-REI.2.Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise.
A-REI (Reasoning with Equations and Inequalities) Solve equations and inequalities in one variable.
- A-REI.3.Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
- A-REI.4.Solve quadratic equations in one variable.
A-REI.4.a. Use the method of completing the square to transform any quadratic equation in x into an equation of the form (x - p)2 = q that has the same solutions. Derive the quadratic formula from this form.
A-REI.4.b. Solve quadratic equations by inspection (e.g., for x2 = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a ± bi for real numbers a and b.
A-REI (Reasoning with Equations and Inequalities) Represent and solve equations and inequalities graphically.
- A-REI.10.Understand that the graph of an equation in two variables is the set of all its solutions plotted in the coordinate plane, often forming a curve (which could be a line).
- A-REI.11.Explain why thex-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the solutions of the equation f(x) = g(x); find the solutions approximately, e.g., using technology to graph the functions, make tables of values, or find successive approximations. Include cases where f(x) and/or g(x) are linear, polynomial, rational, absolute value, exponential, and logarithmic functions.
F-LE (Linear, Quadratic, & Exponential Models) Construct and compare linear, quadratic, and exponential models and solve problems.
- F-LE.4.For exponential models, express as a logarithm the solution to abct = d where a,c, and d are numbers and the base b is 2, 10, or e; evaluate the logarithm using technology.
F-LE (Linear, Quadratic, & Exponential Models) Interpret expressions for functions in terms of the situation they model.
- F-LE.5.Interpret the parameters in a linear or exponential function in terms of a context.
Misconceptions
Student Misconceptions and Common Errors
Students will graph a linear inequality as a line.
- Example: Graph: x + y ≤ 5
- Students struggle with writing linear equations and inequalities for a given situation and identifying the independent and dependent variables.
- Students may confuse the symbols for inequalities (< and >), or may not be sure about when to include equivalence ( < and > ).
- Students struggle with determining how to separate out the objective function and use the graph to find the optimal solution when solving a problem using linear programming.
Vignette
In the Classroom
Solving a linear programming problem in class is very difficult. The correct solution depends on students applying much of the mathematics they have been learning for the past few months. Although linear programming is a great way to integrate many mathematics topics, the success of the students depends much on what they already know.
In the problem below the teacher needs to spend time discussing part a) with the class before moving on to the rest of the problems. Students can make sense of the feasible region before defining it formally. The teacher should guide students to show all possible amounts that fit the time constraint of 12 hours. It is important for students to develop the objective function and apply it to parts of the feasible region when answering parts b) and c). The answers to parts a), b) and c) can be answered without using a Cartesian graph by many students but the constraints introduced in part d) make the problem more complex and encourage the use of the coordinate system.
|
Riley's Mowing Business Riley is a high school student who mows yards in his neighborhood to make money for college. He figures he has up to 12 hours a week free to mow yards. His neighborhood has houses with large yards that take about 45 minutes to mow and houses with small yards that take about 20 minutes to mow. a) Determine all the possible ways that he could select small yards and large yards. Riley decides to charge $40 for the large yards and $25 for the small yards. b) Explain how he should select the number of small and large yards in order to maximize the amount of money he would make. c) Explain which combination of small and large houses will give him the least amount of money. d) Suppose Riley's Dad insists that Riley mow more small yards than large yards. Explain how Riley should choose the number of small and large yards to maximize the amount of money he makes. |
Resources
Teacher Notes
- Students often struggle with describing the solution set for a linear inequality such as x + y ≤ 5. Teachers should emphasize that a graph is a picture for the solutions that make the inequality true and solutions that make it false. Furthermore, solutions are ordered pairs that make the inequality true. Students should be asked to substitute in values of ordered pairs and explain if the ordered pairs are solutions or not.
|
point |
makes inequality... |
Plot the points that make the inequality x + y ≤ 5 true.
|
|
|
A: |
(-2, -5) |
true/false |
|
|
B: |
(0, 4) |
true/false |
|
|
C: |
(5, 0) |
true/false |
|
|
D: |
(5, 5) |
true/false |
|
|
E: |
(-3, 8) |
true/fa lse |
|
|
F: |
(4.5, 1) |
true/false |
|
|
G: |
(4.5, -1) |
true/false |
|
The teacher should then ask students to pick a few more points and eventually they should see that all points that make the inequality true are at or below the line x + y = 5. Many textbooks suggest that students graph linear inequalities by graphing the equality, then picking a test point to determine which side of the line to shade. This procedure is often followed by students without understanding that the shading represents all the ordered pairs that make the inequality true. Teachers need to emphasize that each point that is shaded is a solution.
- Many students who can write an equation to match a situation struggle with writing an inequality for a similar situation.
|
Buying a Mower Joe wants to buy a lawn mover for $800. He charges $15 for each small lawn and $25 for each large lawn. Write an inequality that shows when Joe will make more money than his lawn mower cost. |
Many students are able to write the equality $800=15s+25l$ and explain that $s$ is the number of small lawns mowed and $l$ is the number of large lawn mowed. Furthermore, the student should also explain that the equation $800=15s+25l$ demonstrates the number of small and large lawns that need to be mowed when Joe earns $800 and would the exact amount to pay off his mower. Deciding how the inequality should be placed is difficult. Students struggle with knowing whether to write $800>15s+25l$ or $800<15s+25l$. Students need to make sense of each expression on either side of the inequality before deciding on which of the two inequalities to use. The 800 represents the price of the mower while the $15s+25l$ represents the amount of money Joe will get if he mows $s$ small yards and $l$ large lawns. Teachers need to emphasize what the expressions on each side of an equation or inequality represent so students can make sense of the mathematical sentences they write.
\begin{matrix}
\underbrace{800} &? &\underbrace{15s+25l} \\cost\ of\ mower
& &amount\ earned
\end{matrix}
The students should be able to reason that the amount earned should be more than the cost of the mower and then be able to write the correct inequality. Teachers can then emphasize how to graph and show all the ordered pairs that make the inequality true.
- Escape from the Tomb
In this lesson from NCTM's Illuminations, students are presented with a problem: two bowls are suspended from the ceiling by springs. One bowl is lower than the other. In one bowl, you can only place marbles; in the other bowl, you can only place bingo chips. How many items must be placed in each bowl so that the heights of the bowls are the same? - Supply and Demand
In this grades 9-12 activity from NCTM's Illuminations, students write and solve a system of linear equations in a real-world setting. Students should be familiar with finding linear equations from two points or from the slope and y-intercept. Graphing calculators are not necessary for this activity but could be used to extend the ideas found on the second activity sheet. - Talk or Text
In this lesson from NCTM's Illuminations, students compare different costs associated with two cell phone plans. They write equations with two variables and graph to find the solution of the system of equations. They then analyze the meaning of the graph and discuss other factors involved in choosing a cell phone plan. - Movement with Functions
This unit of three lessons involves students making connections between tables, graphs, equations and real world situations with a motion detector. Lesson 3 asks the students to solve various problems using systems of linear equations.
system of linear inequalities:
Two or more inequalities containing common variable(s). Note: Systems of inequalities sometimes include equations as well as inequalities.
Example:
\begin{cases}
x\geq 0\\y\geq 0
\\x+y< 2
\end{cases}
linear programming:

feasible region: The feasible region is the set of all points which satisfy a system of equations or inequalities. This region is always convex and is shown as the shaded region in the example below:

constraints: Constraints in a system of inequalities include the restrictions found in the inequalities making up the system. In the example below, the constraints are that values in the solution set of the system for x must be < 0, values in the solution set of the system for y must be < 0, and values in the solution set of the system for x and y must satisfy the inequality 3x + 4y < 24.

optimization: When solving a system of linear equations or inequalities, the optimal solution is found at one of the vertices of the feasible region. Testing the coordinates (x,y) in the constraints will determine which vertex provides the optimal solution.
objective function: The objective function for a system of equations or inequalities is the function that is to be optimized; a maximum or minimum value is sought which fits the constraints for the system of equations or inequalities.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- Do students know the difference between equations and inequalities?
- Do students know how solutions of inequalities are displayed?
- How many students can provide at least three solutions to the inequality: 12 < 2a - b?
Materials
- Ellis, M. W., & Bryson, J. L. (2011). A conceptual approach to absolute value equations and inequalities. Mathematics Teacher, 104 (8), 592-598.
- Common Core State Standards (http://www.corestandards.org/the-standards/mathematics)
- Ruddell, M.R., & Shearer, B.A. (2002). "Extraordinary," "tremendous," "exhilarating, "magnificent": Middle school at-risk students become avid word learners with the vocabulary self-collection strategy (VSS). Journal of Adolescent & Adult Literacy, 45, 352-363.
Assessment
1.
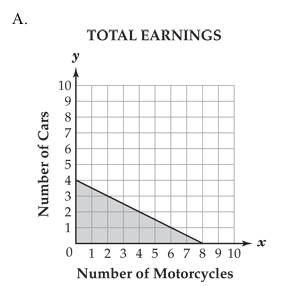
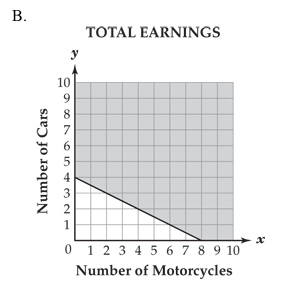
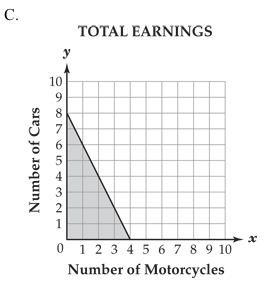
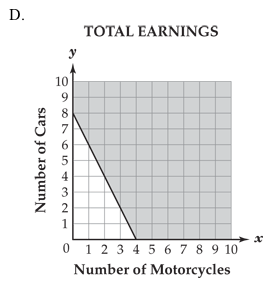
Patrick washes cars and motorcycles. He charges $6 per car and $3 per motorcycle. He earns no more than $24 a week. Which of these graphs best models this situation?
|
|
|
|
|
DOK Level: 2 / Cognitive Level: Understanding
Answer: a
Source: Maryland 2009 High School Assessment - Item 10
http://mdk12.org/assessments/high_school/look_like/2009/algebra/v10.html
2.
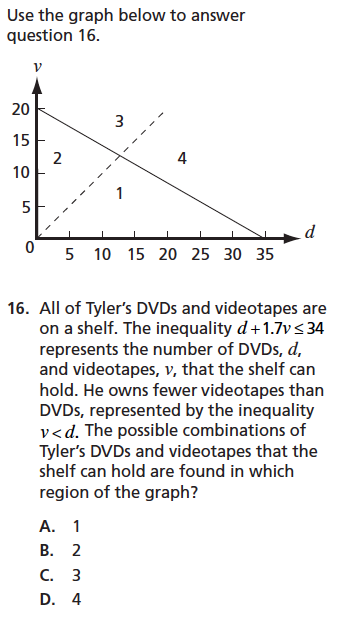
DOK Level: 1 / Cognitive Level: Knowledge
Answer: a
Source: Minnesota MCAII Item Sampler 11th Grade Mathematics - Item 16
http://education.state.mn.us/MDE/Accountability_Programs/Assessment_and_Testing/Assessments/MCA/Samplers/index.html
3.

DOK Level: 2 / Cognitive Level: Understanding
Answer: a
Source: Maryland 2009 High School Assessment - Item 11
http://mdk12.org/assessments/high_school/look_like/2009/algebra/v11.html
4.

DOK Level: 1 / Cognitive Level: Knowledge
Answer: c
Source: Maryland 2009 High School Assessment - Item 17 http://mdk12.org/assessments/high_school/look_like/2009/algebra/v17.html
5.

DOK Level: 3 / Cognitive Level: Application
Answer: See web site for scoring rubric
Source: Maryland 20098High School Assessment - Item 8 http://mdk12.org/assessments/high_school/look_like/2008/algebra/v8.html
Differentiation
- There Has to Be a System for this Sweet Problem
We are confronted with problems on a regular basis. Some of these are easy to solve, while others leave us puzzled. In this lesson, students use problem-solving skills to find the solution to a multi-variable problem that is solved by manipulating linear equations. The problem has one solution, but there are multiple variations in how to reach that solution. This lesson from NCTM's Illuminations also contains suggestions for differentiating based on ability grouping.
- The use of a Cloze sentence or paragraph can be used by teachers to help students develop key vocabulary and meaning from reading a problem. A Cloze sentence is simply a sentence that has words omitted. The teacher gives the students a chance to brainstorm possible words; then the correct word is either determined by the class or is provided by the teacher. The goal of this activity is for students to improve their reading skills. Good readers figure out meanings of key words from the context of the problem, while poor readers do not know what to do when they do not recognize key words and tend to skip over words.
|
Riley's Mowing Business Riley is a high school student who mows _______ in his neighborhood to earn money for college. He figures he has up to 12 hours a week free to mow yards. His neighborhood has houses with large yards that take about 45 minutes to mow and houses with small yards that take about 20 _______ to mow. a) Determine all the possible _______ that he could select small yards and large yards. Riley decides to charge $40 for the large yards and $25 for the small yards. b) Explain how he should select the number of small and large yards in order to _______ the amount of money he would make. c) Explain which combination of small and large houses will give him the least amount of money. d) Suppose Riley's Dad insists that Riley mow more small yards than large yards. Explain how Riley should choose the number of small and large yards to maximize the _______ of money he makes. |
- The solution to the problem below bases the decision only on the amount the person receives each year but does not address the cumulative amount in the account. Students may want to explore this problem by looking at the cumulative amounts instead to see how this perspective might change their solution.
|
How much does it pay? Upon taking his first job, Stuart Martin is given one of the following three options for his retirement plan: Option A: $0.05 the first year $0.15 the second year $0.45 the third year For every year following, triple the amount of the previous year. Option B: $10 the first year $20 the second year $40 the third year For every year following, double the amount of the previous year. Option C: $100,000 the first year $200,000 the second year $300,000 the third year For every year following, add $100,000 to the previous year's amount. Your job is to give Stuart advice about which option is the best. Using mathematics, show him which option is the best for the short term and for the long term. |
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: |
Teachers are: |
|
making connections between representations to make sense of big ideas. |
probing students with questions designed to help them make connections. |
|
making sense of mathematical expressions, equations and inequalities. |
using context as a way to help student make sense of mathematical symbolism. |
|
working individually and in groups, trying to make sense of the mathematics they are learning. |
guiding the students with questions instead of telling them a set of rules to follow. |