9.2.2B Geometric Sequences & Series
Express the terms in a geometric sequence recursively and by giving an explicit (closed form) formula, and express the partial sums of a geometric series recursively.
For example: A closed form formula for the terms $t_{n}$ in the geometric sequence 3, 6, 12, 24, ... is $t_{n}=3(2)^{n-1}$, where n = 1, 2, 3, ... , and this sequence can be expressed recursively by writing $t_{1}$ = 3 and $t_{n}=2t_{n-1}$,for $n\geq 2$.
Another example: the partial sums $s_{n}$ of the series 3 + 6 + 12 + 24 + ... can be expressed recursively by writing $s_{1}=3$ and $s_{n}=3+2s_{n-1}$,for $n\geq 2$.
Recognize and solve problems that can be modeled using finite geometric sequences and series, such as home mortgage and other compound interest examples. Know how to use spreadsheets and calculators to explore geometric sequences and series in various contexts.
Overview
Standard 9.2.2 Essential Understandings
Mathematical modeling is a process that allows students to describe and make sense of the relationship between an independent variable and a dependent variable found in a real-world setting. This standard specifies that high school students should be able to model situations using a variety of functions that include linear, quadratic, exponential, absolute value, inverse, power, square root, and other common functions. Students need to be able to fluidly translate among tables, graphs, and equations of these functions in order to match key features of these functions to real-world situations. The key features that separate these function types include intercepts, asymptotes, restricted domain, and rate of change. As students learn to make connections between the representations of the models and the real-world situation they begin to understand how variables in their life are connected to the mathematics they study in school as well as extend their knowledge of function types themselves.
All Standard Benchmarks
9.2.2.1
Represent and solve problems in various contexts using linear and quadratic functions.
For example: Write a function that represents the area of a rectangular garden that can be surrounded with 32 feet of fencing, and use the function to determine the possible dimensions of such a garden if the area must be at least 50 square feet.
9.2.2.2
Represent and solve problems in various contexts using exponential functions, such as investment growth, depreciation and population growth.
9.2.2.3
Sketch graphs of linear, quadratic and exponential functions, and translate between graphs, tables and symbolic representations. Know how to use graphing technology to graph these functions.
9.2.2.4
Express the terms in a geometric sequence recursively and by giving an explicit (closed form) formula, and express the partial sums of a geometric series recursively.
For example: A closed form formula for the terms tn in the geometric sequence 3, 6, 12, 24, ... is tn = 3(2)n-1, where n = 1, 2, 3, ... , and this sequence can be expressed recursively by writing t1 = 3 and tn = 2tn-1,for n ≥ 2.
Another example: the partial sums sn of the series 3 + 6 + 12 + 24 + ... can be expressed recursively by writing s1 = 3 and sn = 3 + 2sn-1,for n ≥ 2.
9.2.2.5
Recognize and solve problems that can be modeled using finite geometric sequences and series, such as home mortgage and other compound interest examples. Know how to use spreadsheets and calculators to explore geometric sequences and series in various contexts.
9.2.2.6
Sketch the graphs of common non-linear functions such as $f(x)=\sqrt{x}$, $f(x)=|x|$, $f(x)=\frac{1}{x}$, $f(x)=x^{3}$, and translations of these functions, such as $f(x)=\sqrt{x-2}+4$. Know how to use graphing technology to graph these functions.
Benchmark Group B
9.2.2.4
Express the terms in a geometric sequence recursively and by giving an explicit (closed form) formula, and express the partial sums of a geometric series recursively.
For example: A closed form formula for the terms tn in the geometric sequence 3, 6, 12, 24, ... is tn = 3(2)n-1, where n = 1, 2, 3, ... , and this sequence can be expressed recursively by writing t1 = 3 and tn = 2tn-1,for n ≥ 2.
Another example: the partial sums sn of the series 3 + 6 + 12 + 24 + ... can be expressed recursively by writing s1 = 3 and sn = 3 + 2sn-1,for n ≥ 2.
9.2.2.5
Recognize and solve problems that can be modeled using finite geometric sequences and series, such as home mortgage and other compound interest examples. Know how to use spreadsheets and calculators to explore geometric sequences and series in various contexts.
What students should know and be able to do [at a mastery level] related to these benchmarks
- Students should know that there are infinitely many function types that fit a given sequence of numbers. For example, the sequence 3, 6, ... could be arithmetic (linear), geometric (exponential), or any polynomial function. In fact there are infinitely many quadratic functions that contain the points (1,3) and (2,6). The sequence 3, 6, 12, ... is not arithmetic but could be geometric or quadratic. There is only one quadratic function that would match these three points but there are infinitely many cubic functions that would match. Students should not be led to believe that a sequence of three points like 3, 6, 12 means that the sequence is automatically geometric.
- Students should be able to find a recursive and an explicit formula for a geometric sequence given at least two terms of the sequence and the positions of those terms. Students should know that a recursive rule describes the relationships among the values of the independent variable and that an explicit rule describes a relationship between the value of the independent variable and the value of its corresponding dependent variable.
x | y |
|
|
1 | 3 |
| recursive relationship (multiply by 2 or $t_{n}=2\cdot t_{n-1}$, $t_{1}=3$) |
2 | 6 | ||
3 | 12 |
|
|
4 | 24 |
|
|
explicit relationship |
|
| |
- Students should know that a recursive rule contains three parts to be considered complete: the rule, a term, and the domain of the indexing values. The rule $t_{n}=2\cdot t_{n-1}$ is incomplete since there are infinitely many sequences that fit this rule (3, 6, 12, 24, ... and 5, 10, 20, 40, ... both fit this rule). A term value could be $t_{4}=24$, but this is not enough since we do not know the domain of the index variable. A complete rule to describe the geometric sequence 3, 6, 12, 24, ... would be $t_{n}=2\cdot t_{n-1}$, $t_{1}=3$, $n\geq 2$. A convention that is often followed in high school is that the value of the indexing variable is an integer.
- Students should know that the domain of a geometric sequence defined by an explicit rule is often restricted to integers. A common convention used is the domain of the function defined explicitly like $y=3\cdot2^{x-1}$ is the set of real numbers unless otherwise noted.
- Students should be able to notice the recursive relationships found when finding the sum of a geometric sequence and be able to write the relationship with a recursive rule.
n | sn | ||
1 | 3 | = 3 | = 3 |
2 | 3 + 6 | = 9 | = 3 + 2(3) |
3 | 3 + 6 + 12 | = 21 | = 3 + 2(3 + 6) |
4 | 3 + 6 + 12 + 24 | = 45 | = 3 + 2(3 + 6 + 12) |
|
|
|
|
n | sn-1 + tn | ? | 3 + 2 ∙ sn-1 |
Students should be able to write the complete rule for this sum recursively as sn = sn-1 + tn, s1 = 3, n ≥ 2. The rule sn = sn-1 + tn is awkward since it includes two indexing variables. It can be simplified by noticing a pattern in the values of sn column or a general rule if it is expanded cleverly as is demonstrated in the far right column in the table above. In general if a geometric sequence is defined by tn = tn-1∙b, t1 = a, n ≥ 2, then sn = a + b∙sn-1, s1 = a, n ≥ 2. Students should not memorize this formula but be able to follow the logic behind the following expansion using specific numbers.
sn = | a + a ∙ b + a ∙ b2 + a ∙ b3 + ... + a ∙ bn-1 |
| = | a + b(a + a ∙ b + a ∙ b2 + ... + a ∙ bn-2) |
= | a + b(sn-1) |
- Students should be able to identify situations that can be described by a geometric sequence and make sense of these situations by coming up with a model and using graphing utilities and/or spreadsheets to analyze the model.
Work from previous grades that supports this new learning includes:
- As students explore exponential functions with multiplicative rates of change they have to have a robust understanding of multiplication. They need to move past thinking of multiplication simply as repeated addition (i.e. $3\times20=20+20+20$) and the misconception that multiplication always makes a product that is bigger than either factor. They need to understand that there exists a number that make the equation $\square\times20=15$ true. Students need to understand that to find the product of $\frac{3}{4}\times20$ they need to partition $20$ into four equal amounts of five then iterate the five three times as shown on the number line below.
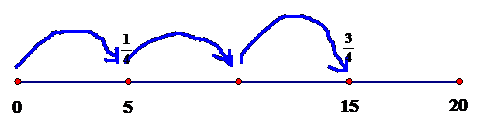
Thinking of multiplication as both a partitioning and iterating process the students will move beyond thinking of multiplication as repeated addition and they will be able to make sense of functions like $f(x)=20\cdot(\frac{3}{4})^{x}$.
- Students in middle school learn to define arithmetic sequences both recursively and explicitly. They learn the notation for both types of rules and that an arithmetic sequence is a linear function with a restricted domain.
NCTM Standards: (those that apply to 9.2.2 are bolded)
(p.296, PSSM) Instructional programs from Pre-K through grade 12 should enable all students to
Understand patterns, relations, and functions. In grades 9-12 all students should
- generalize patterns using explicitly defined and recursively defined functions;
- understand relations and functions and select, convert flexibly among, and use various representations for them;
- analyze functions of one variable by investigating rates of change, intercepts, zeros, asymptotes, and local and global behavior;
- understand and perform transformations such as arithmetically combining, composing, and inverting commonly used functions, using technology to perform such operations on more-complicated symbolic expressions;
- understand and compare the properties of classes of functions, including exponential, polynomial, rational, logarithmic, and periodic functions;
- interpret representations of functions of two variables.
Represent and analyze mathematical situations and structures using algebraic symbols. In grades 9-12 all students should
- understand the meaning of equivalent forms of expressions, equations, inequalities, and relations;
- write equivalent forms of equations, inequalities, and systems of equations and solve them with fluency - mentally or with paper and pencil in simple cases and using technology in all cases;
- use symbolic algebra to represent and explain mathematical relationships;
- use a variety of symbolic representations, including recursive and parametric equations, for functions and relations;
- judge the meaning, utility, and reasonableness of the results of symbol manipulations, including those carried out by technology.
Use mathematical models to represent and understand quantitative relationships. In grades 9-12 all students should
- identify essential quantitative relationships in a situation and determine the class or classes of functions that might model the relationships;
- use symbolic expressions, including iterative and recursive forms, to represent relationships arising from various contexts;
- draw reasonable conclusions about a situation being modeled.
Analyze change in various contexts. In grades 9-12 all students should
- approximate and interpret rates of change from graphical and numerical data.
Common Core State Standards (CCSM)
High School: Functions:
Interpret functions that arise in applications in terms of the context.
· F-IF.4. For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.★
· F-IF.5. Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function.★
· F-IF.6. Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.
Analyze functions using different representations.
· F-IF.7. Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.★
- Graph linear and quadratic functions and show intercepts, maxima, and minima.
- Graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions.
- Graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior.
- (+) Graph rational functions, identifying zeros and asymptotes when suitable factorizations are available, and showing end behavior.
- Graph exponential and logarithmic functions, showing intercepts and end behavior, and trigonometric functions, showing period, midline, and amplitude.
· F-IF.8. Write a function defined by an expression in different but equivalent forms to reveal and explain different properties of the function.
- Use the process of factoring and completing the square in a quadratic function to show zeros, extreme values, and symmetry of the graph, and interpret these in terms of a context.
- Use the properties of exponents to interpret expressions for exponential functions. For example, identify percent rate of change in functions such as $y=(1.02)^{t}$, $y=(0.97)^{t}$, $y=(1.01)^{12t}$, $y=(1.2)^\frac{t}{10}$, and classify them as representing exponential growth or decay.
· F-IF.9. Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a graph of one quadratic function and an algebraic expression for another, say which has the larger maximum.
Misconceptions
Student Misconceptions and Common Errors
- Students have trouble making sense of expressions with exponents that are rational numbers (e.g. $2^{0},9^{\frac{1}{2}},20\cdot (8)^{\frac{2}{3}},5^{-2},-7^{2}$). Making sense of many situations involving exponential functions requires the use of negative and fractional exponents.
- Students struggle using and making sense of functions defined using subscript notation (i.e. $a_{n}=2\cdot a_{n-1},a_{0}=1,n\geq 1$) often used to describe terms in a sequence recursively. Students will often write $n\times2=a$ to describe the doubling sequence $1,2,4,8,...$.
Vignette
In the Classroom
The classroom vignette below is based on an old urban legend about Henry Ford and his paper boy. Henry is said to have offered his paper boy the choice of two plans for his holiday bonus. Plan A is $3000 cash. Plan B consists of giving one cent on the first of December, two cents on the 2nd, doubling that amount to four cents on the 3rd, 8 cents on the 4th, and so on for the 31 days in December. The objective of the lesson is for students to notice that the amount of pennies grows exponentially under plan B and to be able to describe the amount paid both recursively and explicitly.
The story is told to the students and they are asked to choose between the two plans. Monica: I choose Plan A, because I want the money now. Katie: I want Plan A too because I do not want all those pennies. Jimmy: I want Plan B because $3000 is way too much of a tip for a 13 year-old paper boy. Teacher: Work in pairs to determine how much the paper boy would earn if he accepts Plan B. Monica (working with Katie): I have no way to figure this out. Teacher: Try writing out a table.
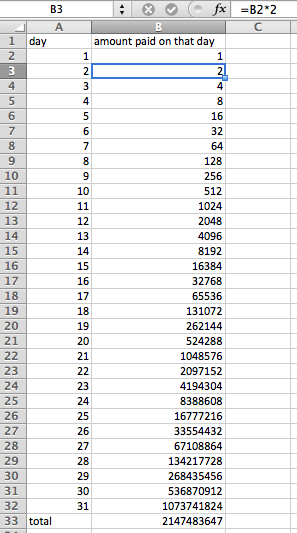
Katie: These numbers are getting big. I am going to use my calculator. [Uses calculator to calculate the amount on the 10th day by taking 512 and multiplying it by 2 to get 1024] Monica: Hey, all we have to do is use the last answer feature on our calculator and press enter 31 times to get the total. [Presses 1, [enter], [×] 2, [enter] 29 more times to get 1073741824.] Wow, I would rather have the 10 million dollars than the $3000. Teacher: What does the 1073741824 represent? Monica: It is the amount the paper boy gets. Katie: No he gets $10,737,418.24 on the 31st. He also gets the pennies from the previous days too. He is going to be really rich. Monica: We have to figure out all the amounts for each day and add them up to get the total amount he would get for the total. After 20 minutes the groups discuss what they found. Katie: Monica and I found that paper boy will get a lot of money. We found that he gets $10 million on the last day and we are in the process of adding the amounts up to get the total sum. James: Wei-Wei and I used a spreadsheet to find the amount on each day and then summed the column to get the amount he received for all 31 days. Plan B is worth $21,474,836.47.
Teacher: What did you enter in the cells to figure this out so fast? James: We entered B2*2 into cell B3 and just dragged it down into the other cells. Teacher: What does B2 stand for? James: B2 is the amount of money paid on the 1st and we multiplied it by 2 to get the amount for the 2nd. The computer automatically changes the formula to B3*2 in cell B4. Teacher: So if you used recursive notation to describe this relationship, what is your rule? James: tn = tn-1•2. Teacher: Is that it? Wei-Wei: Oh yeah, we need t1 = 1 and n ≥ 2. Tony and JB: We did not have a calculator so we just found a formula.
We noticed that the amount paid on the 31st is 230 cents. We did not know how much this would be but knew it was a lot. Teacher: What is the explicit formula for the amount paid on a given day? Tony: It is y = 2x-1. Teacher: What did you get for the sum of all 31 days? Tony: We wrote Sum = s0 + 21 + 22 + 23 + ... + 230 but we do not know what this amount would be equal to. Stella: Gracie and I did a similar table for the sum. We wrote:
We noticed that the sum is always one cent less than the amount on the next day. Teacher: Is this a recursive pattern or an explicit pattern? Stella: I think it is recursive because we used the sum on the previous day to figure out the sum on the next day. I think that the recursive formula would be sn = sn-1 + amount paid on the nth day. Oh and s1 = 1 and n ≥ 2. Gracie: I think we could write sn = sn-1 + tn. We actually found the explicit formula for the sum: Sum 2n - 1 because the sum is always less than the sum on the next day. If there was a December 32nd then that would be 231 cents, therefore the sum would be 231 - 1 cents for the total on the 31st.
|
Resources
Teacher Notes
- The language we use for exponents can be confusing for students. Some books and teachers explain that the expression 23 means "2 times itself 3 times" and proceed to write the equation 23 = 2 • 2 • 2. The expansion does help students make sense of exponential notation but leads to problems with expressions like 21 and 20. If 21means "2 times itself 1 time" then 21could logically be interpreted wrongly as 2 • 2. "2 times itself zero times" seems nonsensical and does little to help students understand that 20 = 1. A better language to use for exponents is to define exponents as the number of factors. The expression 21can be defined as one factor of 2 and it makes sense to students that 21 = 2. Teachers can use the following table to help students make sense of expressions involving exponents.
24 | = |
|
| 23 | = | 8 |
22 | = | 4 |
21 | = | 2 |
20 | = | |
2-1 | = |
|
2-2 | = |
|
|
|
|
Students can make sense of exponential notation by noticing that moving up the table demonstrates the addition of one factor of 2 and results in the value being multiplied by 2. Moving down the table demonstrates removing a factor of 2 and results in each value being divided by 2. Similar patterns can be explored using fractional exponents.
- Subscript notation needs to be developed carefully with students. Students should begin by writing the observed rule in words first. A doubling sequence (i.e. 3, 6, 12, 24, ...) can first be defined by students recursively as "the next term is previous term doubled" or the Fibonacci sequence (i.e. 1, 1, 2, 3, 5, 8, 13, ...) as "the next term is the previous term plus the one before that." After students have had experience describing these rules both orally and in writing then the subscript notation should be introduced. Teachers need to emphasize that ak describes the value of the kth term of the sequence as well as understand that it is the value of the dependent variable when the independent variable is k. Some textbooks avoid the use of subscript notation and write next = now • 2, start = 3 instead of
$t_{n}=2t_{n-1}, t_{1}=3, n>1$. Franzblau and Warner (2001) argue that students can make sense of subscript notation as early as middle school and that the now - next notation might even get in the way of learning subscript notation. The now - next notation is also problematic when describing the Fibonacci sequence and sequences like an = an-1 + 2n + 1, a1 = 1, n ≥ 2.
- Compound Interest Simulator
Use an interactive graphing tool to investigate the relationships among variables involving compound interest.
This three-part e-example from NCTM provides students interactive applets to investigate a real life situation involving recursive relationships using tables, graphs, and equations.
Students use colored water to model a kidney filtering a drug from a system over time. An exponential model is developed both recursively and explicitly.
geometric sequence:
A sequence such as $2+6+18+54+162$ or $3+1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}$, which has a constant ratio between terms. The first term is $a_{1}$, the common ratio is $r$, and the number of terms is $n$.
Explicit Formula: $a_{n}=a_{1}r^{n-1}$
Example 1: $2,6,18,54,162\ has\ a_{1}=2,r=3,\ and\ n=5.$
The explicit formula is $a_{n}=2\cdot3^{n-1}$
Example 2: $3+1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}\ has\ a_{1}=3,r=\frac{1}{3},\ and\ n=6.$
The explicit formula is $a_{n}=3(\frac{1}{3})^{n-1}$
geometric series:
A series such as $2+6+18+54+162$ or $3+1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}$, which has a constant ratio between terms. The first term is $a_{1}$, the common ratio is $r$, and the number of terms is $n$.
Formula: $Sum\frac{a_{1}(r^{n}-1)}{r-1}\ or\ \frac{a_{1}(1-r^{n})}{1-r}$
Example: $3+1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}\ has\ a_{1}=3,r=\frac{1}{3},\ and\ n=6.$
$Sum=\frac{3(1-(\frac{1}{3})^{6})}{1-\frac{1}{3}}=\frac{364}{81}$
explicit rule:
A formula that allows direct computation of any term for a sequence $a_{1},a_{2},a_{3},\cdots,a_{n},\cdots$
Example: $a_{n}=4n-7$
\begin{matrix}
n & 1 &2 &3 &4 &50 &1000\\
a_{n} &-3 &1 &5 &9 &193 &3993
\end{matrix}
recursive rule:
For a sequence $a_{1},a_{2},a_{3},\cdots,a_{n},\cdots$ a recursive formula is a formula that requires the computation of all previous terms in order to find the value of $a_{n}$.
Note: Recursion is an example of an iterative procedure.
Example: \begin{cases}
a_{1}=3\\
a_{n}=2a_{n-1}+5
\end{cases}
\begin{align*}
a_{1} &=3 \\
a_{2} &=2a_{1}+5=2(3)+5=11 \\
a_{3} &=2a_{2}+5=2(11)+5=27 \\
a_{4} &=2a_{3}+5=2(27)+5=59 \\
a_{5} &=2a_{4}+5=2(59)+5=123 \\
etc.
\end{align*}
subscript notation: A letter or symbol written below, and usually to the right, of another symbol for any of various purposes, such as to identify a particular element or elements of a set (such as $a_{1}$ for the first element of the set $a$), or in a chemical formula, to indicate the number of atoms of a particular kind in a molecule (such as $2$ atoms of hydrogen in water, denoted $H_{2}O$).
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- Are my students able to describe recursive and explicit patterns given a well-ordered table of values?
- How do my students explain the differences between a recursive rule and an explicit rule?
- How do I help my students make connections between the recursive rule and the explicit rule?
- Do my students use technology only when I ask them to or do they use it as a tool whenever they decide they need it?
- How do my students use technology at home?
Materials -
Bezuszka, Stanley & Kenney, Margaret. "The three r's: Recursive thinking, recursion, and recursive formulas." In The Roles of Representation in School Mathematics, 2001 Yearbook of the National Council of Teachers of Mathematics, pp. 186-200. Reston, VA: 2001.
Franzblau, Deborah & Warner, Lisa. "From Fibonacci numbers to fractals: Recursive patterns and subscript notation." In Algebra and Algebraic Thinking in School Mathematics, 70th Yearbook of the National Council of Teachers of Mathematics, pp. 211-221. Reston, VA: 2008.
Ruddell, M.R., & Shearer, B.A. (2002). "Extraordinary," "tremendous," "exhilarating, "magnificent": Middle school at-risk students become avid word learners with the vocabulary self-collection strategy (VSS). Journal of Adolescent & Adult Literacy, 45, 352-363.
Lobato - Leaky Faucet
Assessment
Example Item 1
Source: MCAII Item Sampler 11th Grade Mathematics (http://education.state.mn.us/MDE/Accountability_Programs/Assessment_and_Testing/Assessments/MCA/Samplers/index.html) Correct Answer: C Cognitive Level: Understanding
|
Example Item 2
Source: MCAII Item Sampler 11th Grade Mathematics (http://education.state.mn.us/MDE/Accountability_Programs/Assessment_and_Testing/Assessments/MCA/Samplers/index.html) Correct Answer: C Cognitive Level: Understanding
|
Example Item 3
3. The population P of a certain town is given by the equation P = 50,000(1 + r)t, where r is the annual rate of population increase and t is the number of years since 1990. (a) What was the population in 1990? Answer: ____________________ (b) In 2001 the population was 100,000. What was the annual rate of population increase? Answer: ____________________
Source: NAEP Grade 12, 2009, Question M7-3 (http://nces.ed.gov/nationsreportcard/itmrlsx/detail.aspx?subject=mathematics) Correct Answer: (a) Answer: 50,000 (b) Answer: 6.5% (or 0.065) (Accept responses from 6% to 7%, inclusive) Cognitive Level: Hard (32.84% correct)
|
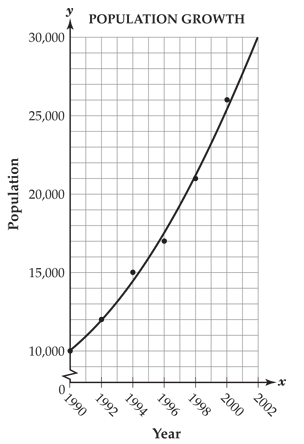
Example Item 4 The scatter plot below shows the population growth of a town. A curve of best fit has been drawn.
According to the curve of best fit, approximately how long did it take for the town's 1990 population to double?
Source: Maryland High School Assessment Algebra/Data Analysis - Item 36 (http://mdk12.org/assessments/high_school/look_like/2009/algebra/v7.html) Correct Answer: C Cognitive Level: |
Differentiation
- Students who struggle with exponential functions typically struggle with multiplication. These students need to develop an understanding of multiplication as both an iterative and partitioning process. Having students draw pictures on a number line showing the results of multiplication will help them develop this understanding. Asking students to show where on the number line the product $5\times a$ would be followed by $\frac{3}{4}\times a$ and $\frac{5}{4}\times a$ would help them develop a deeper understanding of multiplication.

This number line experience can then be expanded to make sense of the calculated value of expressions like $(\frac{3}{4})^{5}\times 8$.
English Language Learners
- Describing the differences between explicit formulas and recursive formulas is difficult for all students including EL's. One strategy to help students make sense of these differences is to do a Word Sort or in this case a formula sort. The table below should be cut into rectangles and the students are then asked to sort the formulas in any way they desire.
an = an-1 + 3 | f(x) = 3 • 5x | tn + 7 = tn+1 |
next = now • 7 | f(x + 1) = f(x) + 3 | an = an-1 • 5 |
tn = 5 • tn-1 + 2n + 3 | an = 2n + 3 | y = 2x + 3 |
After a discussion on sorting results that focuses on the criteria the students chose to sort, the teacher asks the students to sort the formulas into three categories: explicit formulas, recursive formulas, or not sure.
- The standard asks students to model real-world situations using common functions. Some real-world situations that are interesting to students involve relationships that are close to the common functions but somewhat more complex as is demonstrated by the Hurt Knee problem below.
Hurt Knee A student strained her knee in an intramural volleyball game, and her doctor prescribed an anti-inflammatory drug to reduce the swelling. She is to take two 220-milligram tablets every eight hours for 10 days. Her kidneys filter 60% of this drug from her body every 8 hours. How much of this drug is in her system after 10 days?
(National Research Council 1998, p. 80 also in NCTM e-example 7.2 http://www.nctm.org/standards/content.aspx?id=26889) |
As students work the problem they develop the recursive formula an = an-1 • 0.4 + 440, a0 = 440, n ≥ 1 where n stands for the number of 8-hour periods since the player took the drug. Students often write a table first and notice that the amount of drug in the players system reaches a steady state of $773\frac{1}{3}$ mg. Although all students in high school should be able to solve this problem using a table, more advanced students should be able to push this problem further. Students should notice that some of the features of the graph of this function are unlike any of the common functions they have studied.
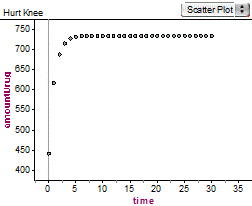
Students should be asked to find the explicit formula for this function. The derivation of the explicit formula involves using the formula for the sum of an infinite geometric series. Student can experiment with the parameters of the situation and determine how the dosage amount and filtration levels impact the steady state and the equation. They should also use this context to explain why this type of function is desirable for medication and study how the mathematics helps you decide what to take if the player misses a dose. They can also go further and create web-plots over time to study when a steady state occurs and when it does not. Students should also be able to find the steady state if one exists symbolically. They should be able to reason that in the equation an = an-1 • 0.4 + 440, the values of an and an-1 are essentially the same if a steady state exists and the steady state can be calculated by solving the equation x = 0.4x + 440 where x is the value of the steady state.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: | Teachers are: |
actively trying to make sense of situations involving exponential growth and decay. | providing problems that ask students to explore exponential growth both recursively and explicitly. Teachers should ask students to use hand-on materials to model exponential growth and decay. |
using technology to study arithmetic trends in the data. | allowing students to use graphing calculators and spreadsheets to explore sequences that grow quickly or decay to a limit. |
describing trends in the data using oral and written language as well as mathematical symbols. | teachers should develop subscript notation appropriately and use correct language to describe meaning. |
Parent Resources
Representing and solving a problem involving exponential growth