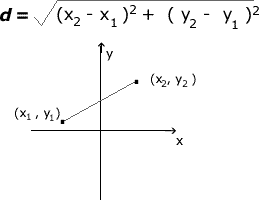8.3.1Pythagorean Theorem
Use the Pythagorean Theorem to solve problems involving right triangles.
For example: Determine the perimeter of a right triangle, given the lengths of two of its sides.
Another example: Show that a triangle with side lengths 4, 5 and 6 is not a right triangle.
Determine the distance between two points on a horizontal or vertical line in a coordinate system. Use the Pythagorean Theorem to find the distance between any two points in a coordinate system.
Informally justify the Pythagorean Theorem by using measurements, diagrams and computer software.
Overview
Essential Understandings/Ideas:
In this learning progression the essential idea is for students to use the Pythagorean Theorem as a tool in problem solving. In this progression, we start with the basic relationship of the side lengths of a triangle and move to giving students situations in which they can classify triangles as acute, obtuse, and right. The focus then becomes the right triangle and the Pythagorean Theorem. It is necessary for them to build a right triangle and use the Pythagorean Theorem to solve the problem.
Initial experiences with Pythagorean Theorem should be CONCRETE by actually finding areas of squares off of each side length and recognizing the relationship between the three squares. This way, students can understand that the theorem is about math objects and their relationship, not just an equation to memorize. The key is developing the understanding of why and how the Pythagorean Theorem is true. Learning is focused on determining distances in right triangle situations. Students will understand the relationship between side lengths of a right triangle and the area of the squares built from those side lengths. Students will understand that the relationship for a RIGHT triangle is a2 + b2 = c2. Students should also explore the relationship that occurs when the triangles are acute to discover a2 + b2 is greater than c2 and obtuse triangles have a relationship where a2 + b2 is less than c2. This will help students understand and apply the idea that the CONVERSE of the Pythagorean Theorem is also true. (NCTM Grade 8 FOCAL POINTS. p.71, 72)


Students will then use the relationship of a2 + b2 = c2 for RIGHT triangles to find missing side lengths and find distances that they cannot "measure." The focus is applying this understanding and using the Pythagorean Theorem as a tool to solve problems. This will require students to draw a right triangle to model a situation and find the distance between two points on a coordinate grid. This is the essential learning that students need in order to understand and develop the distance formula on the coordinate grid.
All Standard Benchmarks - with codes:
8.3.1.1 Use the Pythagorean Theorem to solve problems involving right triangles.
For example: Determine the perimeter of a right triangle, given the lengths of two of its sides. Another example: Show that a triangle with side lengths 4, 5, and 6 is not a right triangle.
8.3.1.2 Determine the distance between two points on a horizontal or vertical line in a coordinate system. Use the Pythagorean Theorem to find the distance between any two points in a coordinate system.
8.3.1.3 Informally justify the Pythagorean Theorem by using measurements, diagrams and computer software.
Benchmark Group A
8.3.1.1 Use the Pythagorean Theorem to solve problems involving right triangles.
For example: Determine the perimeter of a right triangle, given the lengths of two of its sides.
Another example: Show that a triangle with side lengths 4, 5, and 6 is not a right triangle.
8.3.1.2 Determine the distance between two points on a horizontal or vertical line in a coordinate system. Use the Pythagorean Theorem to find the distance between any two points in a coordinate system.
8.3.1.3 Informally justify the Pythagorean Theorem by using measurements, diagrams and computer software.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Use the Pythagorean Theorem to find side lengths of a RIGHT triangle.
- If any two side lengths of a RIGHT triangle are known, the length of the third side can be found by using the Pythagorean Theorem.
- Draw a right triangle to model a situation in which it is difficult to measure one of the distances involved and then use the Pythagorean Theorem to solve.
- Students will be able to use the Pythagorean Theorem to determine the length of the shortest line between two points "as the crow flies" on a coordinate grid.
- Given three side lengths of a triangle, students can determine if the triangle is a right triangle using the converse of the Pythagorean theorem
- Use irrational numbers to represent lengths.
Work from previous grades that supports this new learning includes:
- Use positive exponents specifically when the exponent is 2 (squaring)
- Use square roots
- Find the area of regular and irregular shapes using grid/dot paper
- Classify and interpret rational numbers
- Interpret and estimate irrational numbers (this isn't from another grade but important to learn within this standard or before?)
- Know how to solve for a variable by "undoing"
- Use variables to represent lengths.
- Properties of a right triangle.
- Understand order of operations when solving an equation
- Plot ordered pairs on a coordinate grid.
- Classify angles and triangles as acute, right, and obtuse.
- "Students have an understanding of similarity of geometric relationships. The relationships between the lengths within the object are preserved and use scale factor to solve problems for example, finding lengths in similar figures, distances on maps, and so on..." NCTM Grade 8 Focal Points, p. 50
NCTM Standards:
Geometry:
- create and critique inductive and deductive arguments concerning geometric ideas and relationships, such as congruence, similarity, and the Pythagorean relationship.
- use geometric models to represent and explain numerical and algebraic relationships;
CCSS:
8G7 Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
8G8 Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
8G6 Explain a proof of the Pythagorean Theorem and its converse.
Misconceptions
Student Misconceptions and Common Errors:
- Students often miss the idea that this works for only RIGHT triangles. It is important for students to explore the relationships of the areas of the side length of non-right triangles to clarify that a2 + b2 = c2 is only true for right triangles.
- Students will make the mistake of just adding the side lengths (a + b = c)
- Students will do a2 + b2 = c and forget to take the square root of c2 to find the length of the hypotenuse.
- Students will sometimes substitute the hypotenuse in for a or b instead of c in the equation.
- When finding a length of a segment drawn on dot paper, students count the dots instead of length in units.
Vignette
In the Classroom:
According to NCTM Principles and Standards for School Mathematics, "Technology is essential in teaching and learning mathematics; it influences the mathematics that is taught and enhances students' learning" (NCTM 2000, p. 11). Interactive Web sites can help students to explore dynamic demonstrations of the Pythagorean relationship. In addition, visual and dynamic demonstrations can help students to analyze and explain mathematical relationships.
Teacher: All right students, today we are going to go outside to see if you can discover a very important "rule" in mathematics. Your group will need a tape measure, one of these 5 foot sticks, and a paper and pencil to record your data. When you get outside I need each group to lean the stick against a wall and measure the distance the bottom of the stick is away from the wall and how far the stick went up the wall. Let's set up a table on our paper before we go outside to record our data.. How can we best organize this data?
Student: Ok, we have two measurements we are getting so let's make two columns.
Student: No, I think we will have three measurements. Looks like we will be making a triangle so we have three sides. One will just always be 5 feet.
Teacher: That is correct, technically we will have three lengths that we will be working with. And as always you should try to be very precise with your measurements. Your groups will need to collect data for a variety of position lengths and then see if you can see a relationship between the three lengths that you have.
(Go outside to gather data, or just use a wall in the classroom if weather is not permitting.)
Student: We have collected our data but we can't seem to find a pattern, although we did notice that as the bottom length gets smaller the top length gets larger.
Student: We noticed that too. We also noticed that none of the lengths that we measured were ever larger than 5.
Teacher: Good observations and both will always be true. Does anyone remember why none of the measured lengths will be 5 or larger?
Student: Aren't we working with a right triangle here?
Student: Yeah, we are. Wasn't there a special name for the side opposite from the right angle? I can't remember the name but I remember that it has to be the longest length in the triangle.
Student: I remember, it was called the hypotenuse and the other two sides, the ones we are measuring, are called the legs.
Teacher: That is correct. But now we need to try and look for a relationship between the side lengths. Did anyone measure lengths on the ground that were integers?
Student: We did 1 foot on the bottom.
Teacher: And what did you come up with?
Student: About $4\frac{7}{8}$ feet.
Teacher: Good - Ok, how about anyone else?
Student: We measured 3 feet on the bottom.
Teacher: Ok, stop right there. If you do not have this position of your stick on your paper you need to measure it right now and see what the other length measures.
Student: We got 4 feet. Would it also work if we measured 4 feet on the bottom? Yep, we got three feet on the wall. It's like we are just flipping the triangle.
Teacher: That is correct. Ok, now in your groups see if you can find the relationship with the lengths.
Student: I see it, we have 3 feet, 4 feet, and 5 feet. Just add 1.
Student: But that didn't work for 1 feet, $4\frac{7}{8}$ feet, and 5 feet.
Student: Oh yeah, it should probably work for all lengths.
Teacher: (If a few groups haven't found the relationship yet have them draw a right triangle and then give the hint to draw the squares off of each side length and examine the area).
Student: Oh, I think we found something.
Student: I think we did too.
Teacher: Ok group 1, tell us what you found.
Student: We found that if you draw squares off of each side length and found the areas there was a pattern. The areas of the two squares on the legs added together equal the area of the square on the hypotenuse.
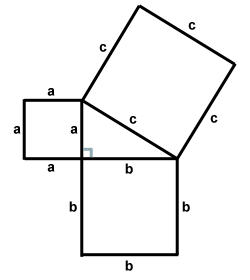
Student: Well that's not what our group found. Our group noticed that if you take each of the lengths of the legs and square them they add to get the hypotenuse length squared.
Student: Aren't those the same thing?
Teacher: Let's examine it with this drawing. What do you think?
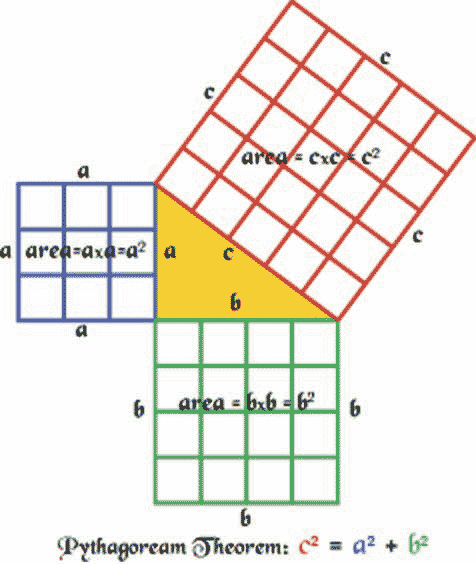
Student: They are the same thing. When we found what the side length squared was it was the same thing the other group did when they found the area of the square.
Teacher: And you guys discovered a well known mathematical theorem known as the Pythagorean Theorem. If the leg lengths of a right triangle are a and b and the hypotenuse is c, then a2 + b2 = c2 or (leg)2 + (leg)2 = (hypotenuse)2. Another way to think about the Pythagorean Theorem is the areas of the squares drawn off the legs added together is equal to the area of the square drawn off the hypotenuse.
Student: I have heard someone say a2 + b2 = c2 but I've never known what they meant.
Teacher: Well, now you do, and we will go back inside and start applying what we have learned with the Pythagorean Theorem to other examples.
*Side note: A teacher could also look at the relationship of the side lengths when the 5 foot stick is placed against an object (a tree, or other leaning object) that is not perpendicular and therefore does not have a 90 degree angle. This activity will lead into discovering the converse of the Pythagorean Theorem.
Resources
Teacher Notes:
- It is essential for students to make the squares and draw the pictures that represent this relationship. This is the concrete connection to this abstract idea. Making this connection will help students to avoid misconceptions like a + b = c or a2+b2=c. Students also need to develop the practice of checking the reasonableness of their answers. For example, the hypotenuse needs to be the longest side, or if the leg lengths are 3 and 4, the hypotenuse cannot be 25. This check will help students realize the misconception that a2+b2=c.
- Sometimes math books complicate the situation by writing the Pythagorean Theorem in a second form with subtraction when finding one of the legs. This may lead students to believe that there are two formulas for the Pythagorean Theorem, when really it is just a second equivalent form of the basic equation.
- The focus is on the relationship among the side lengths and NOT the measurements themselves (NCTM Focal Points 8 p.68).
- "Measurement formulas allow us to rely on measurements that are simpler to access to calculate measurements that are more complicated to access" (Good Questions, Great Ways to Differentiate Mathematics Instruction. p.105).
- The Pythagorean Theorem is the building block of the distance formula. However, this standard is not focused on the distance formula. Requiring students to use the distance formula is not necessary and often confusing to the student if they can find the distance using the Pythagorean Theorem. Once the Pythagorean Theorem is fully developed, having students make connections to the distance formula may be a good extension activity.
- This is a logical place to teach students about rational versus irrational numbers. Although it is not in this benchmark, students need to have an understanding of irrational numbers and square roots in order to make sense of their answers.
Instructional Resources:
- Triangles of Squares: This is an interactive lesson that has students explore the relationship of the squares of the sides of triangles to determine if the triangle is acute, obtuse, or right.The lesson itself is available as a download at the bottom of this resources page.
- PYTHAGOREAN PUZZLE : This is an interactive lesson that has students explore the proof of the Pythagorean Theorem by cutting out squares and triangles and "puzzling" them together to show that the smaller areas add to be the larger area. The puzzel itself is available as a download at the bottom of this resources page.
- Students further explore square roots using the diagonals of rectangles. Using measurement, students will discover a method for finding the diagonal of any rectangle when the length and width are known, which leads to the Pythagorean Theorem. http://illuminations.nctm.org/LessonDetail.aspx?ID=L684
- OnMATH 2008 Volume 6 "The Pythagorean Theorem: Going Beyond a2+b2=c2" by Dr. Katrina Piatek-Jimenez
This lesson provides students with an opportunity to explore the relationships of the squares off of the sides of a variety of triangles not just right triangles. These conditions allow students to really focus in on the relationship of the areas rather than just memorizing the formula. It is a great exploration that uncovers the converse of the Pythagorean Theorem as well. It includes a technology extension exploration with Cabri II Plus. There is also an extension to use with gifted students looking at the area of shapes other than squares off the sides of the triangle. This activity allows students to connect the geometric meaning to the algebraic formula of the Pythagorean Theorem.
Additional Instructional Resources:
- The Pythagorean Theorem relates the lengths of the three sides of a right triangle. In the investigation on this web page, you will learn more about the Pythagorean Theorem and see whether or not it works for triangles that are not right triangles. http://www.keymath.com/x24555.xml
- Good resource for PROOF From NCTM FOCAL POINTS GRADE 8 p.70


- These two videos are a great way for students to see the proof in action with water pouring into the squares built off each side.
Water proof of the Pythagorean Theorem
Not the Pythagorean Theorem (Water proof too)
- Science of NFL football - The Pythagorean Theorem http://www.nbclearn.com/portal/site/learn/nfl/cuecard/51220/
- Animated proof of the Pythagorean Theorem; use website to show students many of the proofs. http://www.usna.edu/MathDept/mdm/pyth.html
-
Title: A Right Triangle with Squares
Students make a square tool and use the tool to investigate the Pythagorean Theorem and its converse with Geometry Sketchpad. http://www.keypress.com/x5596.xml
- Great "real world" connection to Pythagorean Theorem! http://www.aimsedu.org/resources/video/index.html
- Ellis, J. "What's your angle, Pythagoras?" Picture book.
- Board game that can be used as review. Some of the questions involving 45,45,90 and 30,60,90 might not apply. Another review could be students creating their own game card questions to use. http://www.glencoe.com/sec/math/t_resources/gamezone/pdfs/mac3_04/class_ch03.pdf
- Interactive video from PBS. http://www.asset.asu.edu/new/mathactive/lessons/149/look.swf
- Professor R. Smullyan in his book 5000 B.C. and Other Philosophical Fantasies tells of an experiment he ran in one of his geometry classes. He drew a right triangle on the board with squares on the hypotenuse and legs and observed the fact the the square on the hypotenuse had a larger area than either of the other two squares. Then he asked, "Suppose these three squares were made of beaten gold, and you were offered either the one large square or the two small squares. Which would you choose?" Interestingly enough, about half the class opted for the one large square and half for the two small squares. Both groups were equally amazed when told that it would make no difference. (Section pulled from http://www.cut-the-knot.org/pythagoras/index.shtml)
Pythagorean Theorem: It is a theorem that states a relationship that exists in any right triangle. If the lengths of the legs in the right triangle are a and b and the length of the hypotenuse is c, we can write the theorem as the following equation:
a2+b2=c2
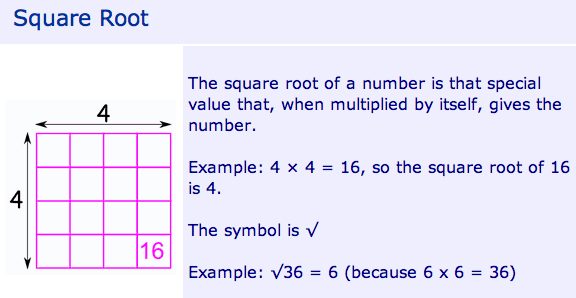
square root: A divisor of a quantity that when squared gives the quantity. For example, 5 is a square root of 25 because 5 × 5 = 25. Another square root of 25 is -5 because (-5) × (-5) = 25. The +5 is called the principle square root of 25.
hypotenuse: In a right triangle, the side opposite to the right angle.
perfect square: A number that is the square of a whole number. For example, 9 is a perfect square since 3 is a whole number and 3 × 3 = 32 = 9.
Pythagorean Triple: A set of three non-zero whole numbers, a, b, and c, such that a2 + b2 = c2. There are infinitely many Pythagorean triples. Some examples are: (3, 4, 5); (11, 60, 61); (5, 12, 13).
right triangle: A triangle with one right angle.
rational number: A number that can be written as $\frac{a}{b}$ where a and b are integers, with b not equal to 0.
converse: The converse of a statement is formed by switching the hypothesis and the conclusion. For example, the Pythagorean Theorem only works for right triangles. So if given three side lengths and the angles are unknown, students can determine that it is a right triangle if the Pythagorean Theorem works.
irrational number: A number whose decimal form is non-terminating and non-repeating. Irrational numbers cannot be written in the form a/b, where a and b are integers. So all numbers that are not rational are irrational. For example, pi or the square root of a non square number. However, students can make their own irrational numbers like .1001000100001000001... or .112123123412345...
leg of a right triangle: Either of the two shorter sides of a right triangle. These two sides together form the right angle in the right triangle.
distance formula: Given the two points (x1, y1) and (x2, y2), the distance between these points is given by the following formula (The Distance Formula is a variant of the Pythagorean Theorem):
Professional Learning Communities:
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- How does the Pythagorean Theorem connect to student understanding of irrational numbers? How can students be helped to make this connection?
- How can teachers help students make the connection between the distance formula and the Pythagorean Theorem and not teach them as two separate entities?
- What evidence exists that students grasp the concrete meaning of the Pythagorean Theorem rather than just memorizing the formula?
- Understanding the Pythagorean Relationship Using Interactive Figures This link provides teachers with an opportunity to look at a computer-generated model showing the proof. Reflection questions are included for teachers to discuss.
From NCTM Principles and Standards.
Materials:
Tilted Squares, Irrational Numbers, and the Pythagorean Theorem Article from NCTM Mathematics Teaching in the Middle School, August 2009. Volume 15, Issue 1, pg. 57 (note: Membership in NCTM is required to access this resource).
References:
AIMS Education Foundation. Triangles of Squares and Pythagorean Puzzle.
Focal Points Grade 8, NCTM.
Small, M. Good Questions: Great Ways to Differentiate Mathematics Instruction (NCTM).
Assessment
Website includes 9 multiple choice questions with answer key; also includes some converse questions. (http://www.quantiles.com/)
1.
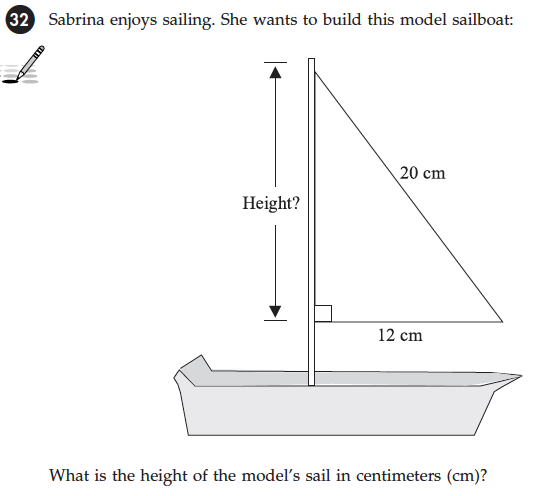
FCAT 2006 Mathematics Released Test 2006 Florida Department of Education (gridded response item).
2.
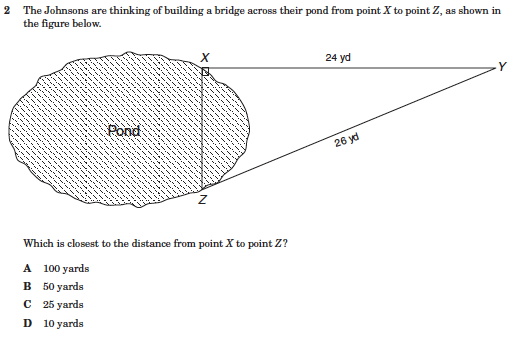
TAKS (Texas Assessment of Knowledge and Skills) Mathematics, Grade 8, 2010 released items.
3.

#17 from MN Math MCA grade 8 item sampler
4.
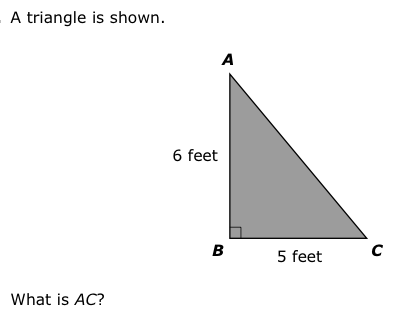
#24 from MN Math MCA grade 8 item sampler
5. A boat sets sail from an island located at (4, 12) on a map. Its destination is the boat landing located at (6, 2). What is the shortest distance that the boat will travel? (Differentiated question - What is the shortest distance the boat will travel if each unit on the grid is 0.5 mile? ANS 5.1 mi)
6. Given three side lengths of a triangle, determine if the triangle is a right, acute, or obtuse triangle.
a) 2ft, 4ft, 5 ft b) 6 in, 8in, 10in c) 10m, 5m, 10m
correct answers: a) obtuse b) right c) acute
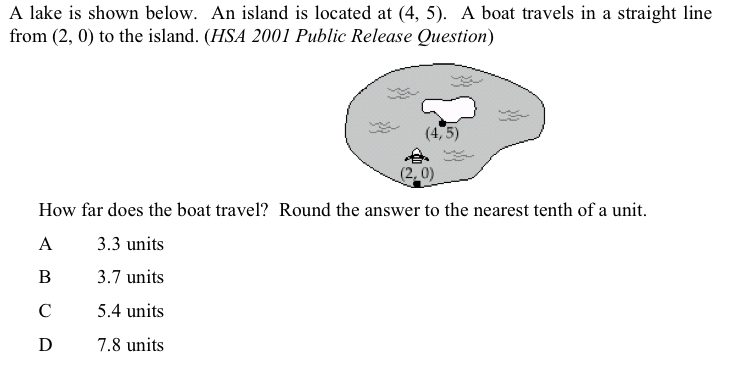
7. A lake is shown below. An island is located at (4,5). A boat travels in a straight line from (2,0) to the island. (HSA 2001 Public Release Question)
8. A diagram of a baseball field is shown below. The infield is a square that measures 90 feet on each side (HSA 2001 Public Release Question)
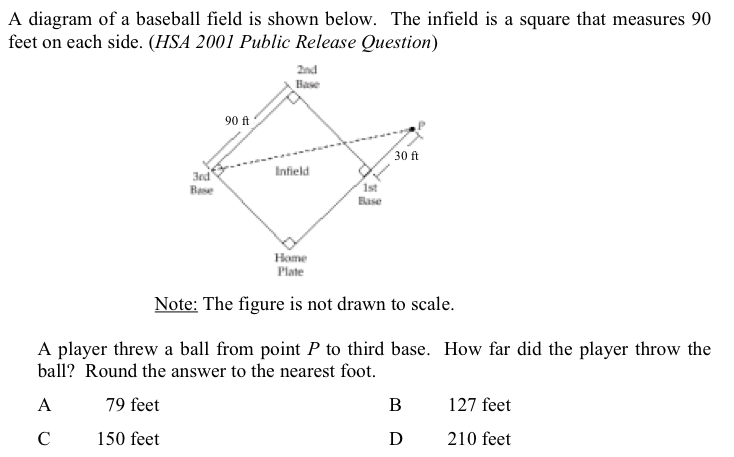
Correct answer: C
9. Jill wants to plant flowers in a triangular plot. She has three lengths of plastic garden edging that measure 8 feet, 15 feet, and 17 feet. Determine whether these pieces form a right triangle. Explain.
Correct answer: Yes. Sample explanation: Because 82 + 152 = 172, the pieces fit together to form a right triangle by the converse of the Pythagorean Theorem
Differentiation
Struggling Students:
- Encourage students to keep drawing the squares off the side lengths to reinforce the concrete. It's not necessary to make them use just the formula. (This is good for ALL students!)
- When teaching Pythagorean Theorem, hands-on activities involving math manipulatives are typically helpful to ELL students because the lesson involves multiple learning modalities and does not require a student to rely solely upon his/her ability to understand verbal instruction.
- Rewrite word problems using fewer and easier words so that ESL students can practice both math and language skills without being stuck on what a particular phrase or word means as they read the problem. Keep the sentences short and to the point. Take out extra detail that is not needed to convey the gist of the problem.
- Using a graphic organizer is a powerful strategy for helping all students and it especially helps English Language Learners with organizing and remembering information. Because graphic organizers arrange details in a visual form, they help students retain concepts. a graphic organizer for Pythagorean Theorem
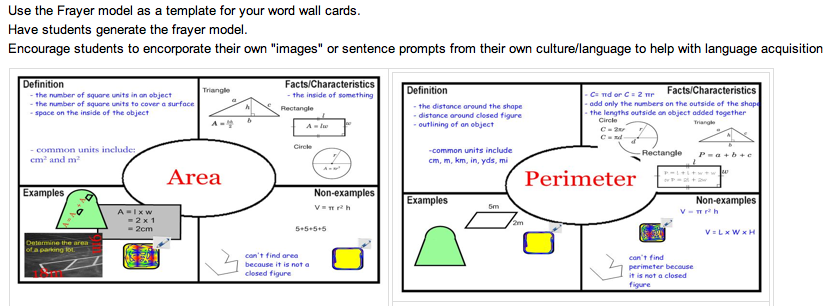
The image above was taken from: http://math-on-the-move.wikispaces.com/ELL+Math
- Lesson from OnMATH: Online Journal of School Mathematics NCTM website. Pythagorean Theorem: Connecting Interactive Websites by Cheng-Yao Lin. (2006-2007, Volume 5 Number 1)
This lesson focus is on different proofs of the Pythagorean Theorem from different cultures. There is a brief history about the Pythagorean Theorem and then it links you to multiple interactive websites that illustrate and animate the different proofs. The technology of this is important.
Some possible extensions of this lesson (from the proof lesson above) include the following:
- Consider an + bn=cn, n > 2. Does this formula work just like the Pythagorean Theorem? Can you find an interactive Web site with a proof of this theorem?
- Consider the converse of the Pythagorean Theorem and generalize the theorem to shapes other than triangles.
- Can you find the Pythagorean Theorem in everyday life? What real world applications of Pythagorean Theorem are there? How about finding the distance from one corner of a class room to all the other corners of a classroom; use concrete, practical/realistic, introduction into three dimensions.
- One side of a right triangle is 5 units long. What could the other sides be? (Open question).
- Math Tools book, p.237-238. "Go Fly a Kite" choice activities for gifted.
- Teach simplifying radicals.
- Special Triangles 30-60-90 and 45-45-90.
- Parachute activity (only the reflection questions at the end are leveled).
Parents/Admin
Administrative/Peer Classroom Observation:
|
Students are: (descriptive list) |
Teachers are: (descriptive list) |
|
drawing the right triangle to represent the information given - drawing the squares off each side length - finding the areas of the squares. Then using the areas of two of the squares to find the side length of the other square. |
emphasizing that even though a problem can be solved by substituting the given values into the formula and solving for the unknown variable, students will benefit from drawing a sketch of the triangle. Doing this reinforces students identifying the legs and the hypotenuse. |
|
using the pictoral representation of the Pythagorean Theorem when they are stuck or having trouble with the algebraic formula. |
asking students to make observations about the relationships of the area of the squares off the side lengths of each triangle. |
|
|
giving students problems to solve that involve real world applications of the Pythagorean Theorem. Include distances that they would not be able to measure; for example, the distance across a river or ravine. |
|
connecting the Geometric representation with the Algebraic representation
Figure 3.13 p.69 NCTM Focal Points 8 |
providing students with problems in which the student needs to draw a diagram to represent the information given, and then decide to use the Pythagorean Theorem because they created a right triangle for their diagram. |
|
plotting points on a coordinate grid and connecting the points with a line segment. Then they are drawing a right triangle with the hypotenuse being the line that they drew. They are then finding the vertical and horizontal distances (lengths of the legs) and using the Pythagorean Theorem to find the length of the hypotenuse (length of the original line segment). |
encouraging students to go back to drawing squares if they are having trouble using the algebraic formula of the Pythagorean Theorem. |