7.1.2B Problem Solving with Rational Numbers
Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest.
Use proportional reasoning to solve problems involving ratios in various contexts.
For example: A recipe calls for milk, flour and sugar in a ratio of 4:6:3 (this is how recipes are often given in large institutions, such as hospitals). How much flour and milk would be needed with 1 cup of sugar?
Overview
Standard 7.1.2 Essential Understandings
In this standard, students will develop a unified understanding of number, recognizing fractions, decimals (that have a finite or a repeating decimal representation), and percents as different representations of rational numbers. Students extend addition, subtraction, multiplication and division to all rational numbers, maintaining the properties of operations and the relationships between addition and subtraction, and multiplication and division. By applying these properties, and by viewing negative numbers in terms of everyday contexts (e.g., amounts owed or temperatures below zero), students explain and interpret the rules for adding, subtracting, multiplying and dividing with negative numbers.
The focus of instruction at the 7th grade level is on being able to comfortably translate between decimal and fractional forms of a number for both positive and negative values. Students should be able to compare numbers and manipulate the values to derive other forms of the numbers to make comparing less inhibiting and more accessible. Students will also use ratios and proportional reasoning to solve problems in various contexts. Students will be able to use information given to help find missing values. Their knowledge of equivalent fractions and scaling will enable them to use ratios and solve proportions.
All Standard Benchmarks
7.1.2.1
Add, subtract, multiply and divide positive and negative rational numbers that are integers, fractions and terminating decimals; use efficient and generalizable procedures, including standard algorithms; raise positive rational numbers to whole-number exponents.
7.1.2.2
Use real-world contexts and the inverse relationship between addition and subtraction to explain why the procedures of arithmetic with negative rational numbers make sense.
7.1.2.3
Understand that calculators and other computing technologies often truncate or round numbers.
7.1.2.4
Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest.
7.1.2.5
Use proportional reasoning to solve problems involving ratios in various contexts.
7.1.2.6
Demonstrate an understanding of the relationship between the absolute value of a rational number and distance on a number line. Use the symbol for absolute value.
7.1.2 Group B - Problem Solving with Rational Numbers
7.1.2.4
Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest.
7.1.2.5
Use proportional reasoning to solve problems involving ratios in various contexts. For example, a recipe calls for milk, flour and sugar in a ratio of 4:6:3. (This is how recipes are often given in large institutions, such as hospitals.) How much flour and milk would be needed with 1 cup of sugar?
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Understand that simple interest does not use interest earned as new principal, but compound interest does;
- Model addition and subtraction of integers with physical materials and the number line;
- Perform calculations with and without the use of a calculator;
- Understand the rules for calculating with positive and negatives;
- Understand calculating with positive exponents;
- Scale values up and down;
- See the relationship as a proportional relationship;
- Use ratios accurately;
- Compare ratios;
- Be able to differentiate mathematical characteristics of proportional thinking from nonproportional contexts;
- Know the mathematical characteristics of proportional situations.
Work from previous grades that supports this new learning includes:
- Use and read output on a calculator;
- Know how to change percents to decimals and decimals to percents;
- Know how to calculate a percent of a number, such as 25% of 1000;
- Use and find percents;
- Use and find fractions and equivalent values;
- Multiply and divide;
- Input into a calculator, using correct keystrokes;
- Perform mental math;
- Understand equivalent fractions;
- Scale up and down;
- Use ratios;
- Know multiplication facts to 12's;
- Be proficient at problem solving ;
- Know how to work backwards;
- Understand and use the terms including numerator, denominator, greatest common factor and least common multiple;
- Know how to simplify fractions.
- Make use of estimation strategies.
NCTM Standards
Understand numbers, ways of representing numbers, relationships among numbers, and number systems:
- Work flexibly with fractions, decimals, and percents to solve problems;
- Understand and use ratios and proportions to represent quantitative relationships.
Understand meanings of operations and how they relate to one another:
- Understand the meaning and effects of arithmetic operations with fractions decimals, and integers;
- Understand and use the inverse relationships of addition and subtraction, multiplication and division, and squaring and finding square roots to simplify computations and solve problems.
Compute fluently and make reasonable estimates:
- Select appropriate methods and tools for computing for computing with fractions and decimals from among mental computation, estimation, calculators or computers, and paper and pencil, depending on the situations and apply the selected methods;
- Develop and use strategies to estimate the results of rational-number computations and judge the reasonableness of the results.
Common Core State Standards (CCSS)
7.NS (The Number System ) Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers.
- 7.NS. 1. Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram;
- 7.NS.1.b. Understand p + q as the number located a distance |q| from p, in the positive or negative direction depending on whether q is positive or negative. Show that a number and its opposite have a sum of 0 (are additive inverses). Interpret sums of rational numbers by describing real-world contexts;
- 7.NS.1.c. Understand subtraction of rational numbers as adding the additive inverse, p - q = p + (-q). Show that the distance between two rational numbers on the number line is the absolute value of their difference, and apply this principle in real-world contexts;
- 7.NS.1.d. Apply properties of operations as strategies to add and subtract rational numbers;
- 7.NS.2. Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers;
- 7.NS.2a. Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (-1)(-1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts;
- 7.NS.2.c. Apply properties of operations as strategies to multiply and divide rational numbers;
- 7.NS.3. Solve real-world and mathematical problems involving the four operations with rational numbers.
6.NS (The Number System) Apply and extend previous understandings of numbers to the system of rational numbers.
- 6.NS.7c. Understand ordering and absolute value of rational numbers. Understand the absolute value of a rational number as its distance from 0 on the number line; interpret absolute value as magnitude for a positive or negative quantity in a real-world situation. For example, for an account balance of -30 dollars, write |-30| = 30 to describe the size of the debt in dollars.
- 6.EE (Expressions and Equations) Apply and extend previous understandings of arithmetic to algebraic expressions.
6.EE.1. Write and evaluate numerical expressions involving whole-number exponents.
7.EE (Expressions and Equations) Use properties of operations to generate equivalent expressions.
- 7.EE.3. Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations as strategies to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies.
- 7.RP (Ratios and Proportional Relationships) Analyze proportional relationships and use them to solve real-world and mathematical problems.
7.RP.3. Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.
Misconceptions
Student Misconceptions and Common Errors
- Students may not realize that finding the percent of a number always involves division.
- Students incorrectly enter the percent into the calculator instead of the decimal value, and thus get a value that does not make sense. Many students do not know how to use the % key on a calculator.
- Students get confused with the difference between simple and compound interest.
- Students may not realize that using a proportion is the only way to solve these problems.
- Students want to use addition to get equivalent values, not multiplication.
- Students forget how to multiply with fractional values.
- If using a fractional scale factor (cutting a recipe in $\frac{1}{2}$), students may just add $\frac{1}{2}$ to the values they have, instead of dividing all the values by 2.
Vignette
In the Classroom
In this vignette, students will mix juice.
Mixing Juice
Teacher: How many of you have made orange juice from a can before?
Student 1: I make it all the time.
Student 2: My mom makes ours.
Others raise their hands to indicate they have either made it or helped make it.
Teacher: When you made juice or helped, what did you have to do?
Student 3: Make sure we didn't add too much water or it wouldn't taste very good.
Teacher: Anything else?
Student 2: Make sure we add enough water or it would be too sour and strong tasting.
Teacher: Today we are going to look at some different recipes for different juice mixes. Each recipe is different from the others, so we are going to use our math skills and see if we can decide which juice would be the most orangey, and which would be the least orangey.
Student 1: Won't it depend on the brand of juice we use, too?
Teacher: You are right; that could be a factor, and that could be something we explore at a different time, but for today, we are going to assume that all the juices are the same brand, so that won't be a factor.
Teacher: OK, here is your information. Cam and Scott are in charge of making juice for the 200 students at camp. They mix water and frozen concentrate to make the juice. They were given the following recipes from different campers:
|
Mix S 2 cups orange concentrate 3 cups water |
Mix T 3 cups orange concentrate 4 cups water |
|
Mix U 3 cups orange concentrate 6 cups water |
Mix V 5 cups orange concentrate 8 cups water |
Teacher: OK, your task is to figure out which one is the most orangey. Good luck!
As the teacher circulates around, she hears some of the following conversations.
Student 1: I think Mix V will be the most orangey because it has 5 cups of concentrate, and no other juice has that much, so it has to be the most orangey.
Student 2: I think Mix S and Mix T will be the same because they each have only one more cup of concentrate than juice, so they should taste the same, shouldn't they?
Teacher: Well, how about if we use some concepts we've talk about in class before. What could we do that might help us?
Student 3: Write them as fractions?
Student 2: Find out what percent of each is concentrate?
Student 1: We could write ratios for each recipe.
Teacher: OK. It sounds like we have many ideas. There are multiple ways to do this problem. Just make sure you understand what you are doing, and if you get an answer, make sure you know what it represents in terms of the problem.
Student 1: Well for Mix S, $\frac{2}{3}$ of the juice is concentrate.
Teacher: Let's look at that again. While fractions offer one way of working on this problem, what you said is not accurate. Remember what you know about fractions. If you say that $\frac{2}{3}$ of the juice is concentrate, then which number in the fraction tells you how many total cups are in the juice?
Student 2: Well, the denominator is the total, so the total would be 3 cups. In Mix S, though, there are 3 cups of concentrate AND 2 cups of water, so there's really 5 cups of ingredients in the juice.
Teacher: So is $\frac{2}{3}$ of Mix S concentrate?
Student 1: No, I guess it isn't. But shouldn't we be able to use the fraction $\frac{2}{3}$?
Teacher: Let's talk about that. If we use $\frac{2}{3}$, what does the 2 represent?
Student 3: The 2 cups of water.
Teacher: And what does the 3 represent?
Student 4: The 3 cups of concentrate.
Teacher: So if we wanted to know what fraction is concentrate, what fraction would we use?
Student 2: $\frac{2}{5}$, because 5 is the total amount of cups in the juice and 2 is the number of cups of concentrate.
Teacher: OK. Keep working and I'll come back to you. Again, we are trying to figure out which one is the most orangey.
The teacher continues to circulate around the room, listening to conversations that different groups are having.
Teacher: Who has an idea here? Which mix does your group think is the most orangey?
Student 2: We think it is Mix T. We set up ratios of concentrate to water, and compared the decimal values. So this is what we got:
|
Mix S $\frac{2}{3}$= .6667 |
Mix T $\frac{3}{4}$ = .75 |
|
Mix U $\frac{3}{6}$ = .50 |
Mix V $\frac{5}{8}$= .625 |
Teacher: What do those decimal values represent?
Student 2: The ratio of concentrate to water.
Teacher: Did anyone do this another way?
Student 3: We found out what percent of the juice was concentrate. So here is what we got. We agree that Mix T is the most orangey.
|
Mix S $\frac{2}{5}$ = .4 = 40% |
Mix T $\frac{3}{7}$ = .4285714 = about 43% |
|
Mix U $\frac{3}{9}$ = .33=33% |
$\frac{5}{13}$ = 0.3846 = about 38% |
Teacher: So, we can see from these two strategies that Mix T is the most orangey. Which one is the least orangey?
Student 1: Mix U. If you look at the percent that is concentrate, we can see that Mix U has the least percent of concentrate, so it is the least orangey.
Teacher: Let's move on to the next part of the problem. Assume each camper gets $\frac{1}{2}$ cup of juice. For each mix, you need to now figure out how many batches are needed to be made to serve all of the campers. Remember, there are 200 campers.
Student 4: I think we need to first figure out how many cups are in each batch of juice.
Teacher: Why would you need to know that?
Student 4: So we can scale the recipe up to make enough to feed the campers.
Teacher: Good thought process. Go ahead and give it a try and let me know how it goes.
Student 3: Can't we just multiply 200 by $\frac{1}{2}$ to get 100? We need 100 cups of juice made.
Teacher: OK. You are right that you need 100 cups, but that is 100 cups of juice. That doesn't say how many cups of each of the 2 ingredients you need.
Student 3: Oh. That's right. We need to do that. Hmm. Maybe putting the information into tables could help us.
|
|
Concentrate |
Water |
Total |
|
Mix S |
2 |
3 |
5 |
|
Mix T |
3 |
4 |
7 |
|
Mix U |
3 |
6 |
9 |
|
Mix V |
5 |
8 |
13 |
|
|
Number of batches |
Cups of concentrate and water |
|
Mix S |
100/5 = 20 |
20 x 2 = 40 20 x 3 = 60 |
|
Mix T |
100/7 = 14.29 (so 15 batches are needed |
15 x 3 = 45 15 x 4 = 60 |
|
Mix U |
100/9 = 11.1 |
12 x 3 - 36 12 x 6 = 72 |
|
Mix V |
100/13 = 7.7 |
8 x 5 = 40 8 x 8 = 64 |
Teacher: Nice. Any other way this could have been figured out?
Student 4: We used proportional reasoning to solve it. We knew that we needed 100 cups total. We also knew how many batches we needed. So, we knew we needed 100 cups total, and there were 5 total cups in the batch made. Since we needed two cups of concentrate, then we can scale that up. Here's the proportion we set up:
$\frac{2}{5}$ = $\frac{x}{100}$
|
Concentrate (value of x) |
Water (100 - x) |
|
|
Mix S $\frac{2}{5}=\frac{x}{100}$ |
40 c. |
60 c. |
|
Mix T $\frac{3}{7}=\frac{x}{100}$ |
43 c |
57 c. |
| Mix U $\frac{3}{9}=\frac{x}{100}$ |
33 c. |
67 c. |
| Mix V $\frac{5}{13}=\frac{x}{100}$ |
38 c. |
62 c. |
Student 4: So, we can solve and get 40 for x, just like the other group did. So, we need 40 cups of concentrate and 60 cups of water. We did that same process for the rest of them, too, like our table shows. By doing it our way, we won't have as much left over, because they rounded the number of batches, and we set up proportions so we have a closer number of cups that would be needed. We still have Mix T using the most concentrate in proportion to the amount of water used.
Teacher: OK. Nice work! To finish the lesson, here is your final task: Which of the following will taste most orangey: 2 cups of concentrate and 3 cups of water; 4 cups of concentrate and 6 cups of water; or 10 cups of concentrate and 15 cups of water?
The students use various strategies that were discussed in class.
Teacher: Anyone have an answer?
Student 2: I think they are all the same orangey-ness?
Teacher: How could that be if they all have different numbers of concentrate and water?
Student 1: Because when we compared all of the ratios, they were equivalent: 2 to 3 is equivalent to 4 to 6, is equivalent to 10 to 15. If we write them all as fractions we can see that even better.
Teacher: Can you come up to the board and show us what you are doing?
Student 1: Sure. Here is what I did:
$\frac{2}{3}$ = $\frac{4}{6}$ = $\frac{10}{15}$
They all simplify to being the same concentrate, $\frac{2}{3}$, so, they are all proportional to one another.
Teacher: Nice job today. We will review this tomorrow.
Resources
Teacher Notes
- To find percent increase or percent decrease, have the students subtract the two values being compared. Then, have them take that answer and divide it by the beginning value to get the ratio of change to starting value. Multiply this value by 100 to get the percent change. For example, the population changed from 1000 to 1150. What was the percent increase? The students would subtract 1150 - 1000 to get 150. They then need to divide 150 by 1000 to get 0.15. Multiply this value by 100 (change a decimal to a percent), and the percent increase is 0.15 × 100 which equals 15%. This website provides a calculator that will do this.
- The scale on a map suggests that 1 centimeter represents an actual distance of 5 kilometers. The map distance between two towns is 8 centimeters. What is the actual distance? In this situation, a table can help highlight this relationship.
|
Map Distance |
1 cm |
2 cm |
3 cm |
4 cm |
|
Actual Distance |
5 km |
10 km |
15 km |
20 km |
Drawing pictures may help students see that the rate is a scalar concept.
- To help students learn the difference between compound and simple interest, work on simple interest first. In simple interest, the amount of interest earned is proportional to the number of months invested. For example, a deposit of $500 in an account earns 1% simple interest each month. After 1 month, $5 of interest would be earned, because $500×1% = $5. ($500x0.01 = $5). After two months, there will be $10 of interest earned. Interest is only earned on the original deposit with simple interest. With compound interest, interest is not only calculated on the original deposit, but also the interest that has previously been earned. So, one month, the interest earned would be $500x1% = $5. The balance after that first month is $505. After two months, the interest is earned on the total balance of $505. As shown in the table, the amount added each month is not constant, therefore, compound interest earned is not an example of a proportional relationship, whereas simple interest earned is showing a proportional relationship.
|
Number of Months |
Simple interest earned |
Compound interest earned |
|
0 |
0 |
0 |
|
1 |
5 |
5 |
|
2 |
10 |
10.05 |
|
3 |
15 |
15.15 |
|
4 |
20 |
20.30 |
|
5 |
25 |
25.51 |
|
10 |
50 |
52.31 |
- Proportion problems
This website will explain proportions, provide examples, and provides sample problems. - Ratios and proportions
This site includes ratios, comparing ratios, and proportions. - Ratio and proportion factsheets
- Ratios and proportions in everyday life
This site addresses ratios and proportions and how knowledge of these mathematical concepts is used in everyday life. It includes lesson plans, animation, online and printable worksheets, online exercises, games, quizzes, and a link to eThemes Resource on Math: Equivalent Ratios. - Real-world proportions
This site includes problems with solving proportions (algorithms) and real-world applications. - Math in daily life: Cooking by numbers
This webpage that helps make a connection between proportions and the real-life situation of cooking. - Burns, M., and Sheffield, S. (2004). Jim and the Beanstalk. In Math and Literature (p. 60). Sausalito, CA: Math Solutions Publications.
- Burns, M., and Sheffield, S. (2004). How Big is a Foot. In Math and Literature (p. 47). Sausalito, CA: Math Solutions Publications.

- interest: fee paid on loans or earned on invested money, based on the principal amount and the interest rate.
- simple interest: interest paid only on the original principal, not on the interest accrued.
- compound interest: interest computed on accumulated interest as well as on the principal.
- proportion: an equation which states that two ratios are equal; a relationship between two ratios.
Example: $\frac{\text{hours spent on homework}}{\text{hours spent in school}}=\frac{2}{7}$
Note that this does not necessarily imply that "hours spent on homework" = 2 or that "hours spent in school" = 7. During a week, 10 hours may have been spent on homework while 35 hours were spent in school. The proportion is still true because $\frac{10}{35}=\frac{2}{7}$.
- proportional reasoning: a mathematical way of thinking in which students recognize proportional versus non-proportional situations and can use multiple approaches, not just the cross-products approach, for solving problems about proportional situations.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What conclusions can be drawn about the student's understanding of applying relationships to solve problems in various contexts?
- Can students scale values up or down and understand why they are doing it?
- Can students tell if a relationship is proportional by looking at the verbal description of it, or do they need to mathematically figure it out?
- Are students able to transfer prior knowledge about equivalent fractions to the concept of proportionality?
- Do students understand why their procedures work?
- What connections have been made as students explored the mathematical characteristics of proportional situations?
- What models would help students in understanding the concepts addressed in the lesson?
- What aspects of proportional relationships are students still struggling with?
Materials
Cramer, K. & Post, T. (1993, February). Making connections: A case for proportionality. In Arithmetic Teacher, 60(6), 342-346.
- Massachusetts Comprehensive Assessment System Spring 2010 Test Items
http://www.doe.mass.edu/mcas/2010/release/g7math.pdf - Absolute value
http://www.purplemath.com/modules/absolute.htm - Adding and subtracting negative numbers
http://www.purplemath.com/modules/negative2.htm - Lappan, G., Fey, J., Fitzgerald, W., Friel, S., Philips, E. (2009). Accentuate the Negative, CMP2. Pearson Prentice Hall.
- Lappan, G., Fey, J., Fitzgerald, W., Friel, S., Philips, E. (2009). Comparing and Scaling, CMP2. Pearson Prentice Hall.
- Rational Number Project: Proportional reasoning: the effect of two context variables, rate type, and problem setting
http://www.cehd.umn.edu/rationalnumberproject/89_6.html - Dacey, L.S., and Gartland, K. (2009). Math for All: Differentiating Instruction. Sausalito, CA: Math Solutions.
Assessment
1.

Answer: a
DOK: Level 3
Source: Minnesota Grade 7 Mathematics MCA-III Item Sampler Item, 2011, Benchmark 7.1.2.4
2.
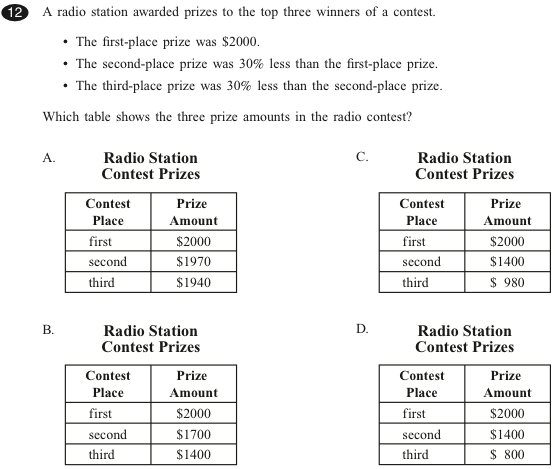
Answer: c
DOK: Level 3
Source: Massachusetts Comprehensive Assessment System Release of Spring 2009 Test Items
3.
Assume you borrow $900 at 7% annual compound interest for four years.
- How much money do you owe at the end of the four years? Show or explain your work.
- What is the total interest you will have to pay? Show or explain your work.
Answers: Part A: $900 + $252 = $1179.72; Part B: $279.72
DOK: Level 2
Source: Test Prep: Modified from MCA III Test Preparation Grade 7, Houghton Mifflin Harcourt Publishing Company, Attn: Contracts, Copyrights, and Licensing, 9400 South Park Center Loop, Orlando, FL 32819.
4.
Tim is mixing 1 L of juice concentrate with 5L of water to make juice for his 10 guests. After he pours the mix into 10 different cups, he realizes that the juice is not sweet enough, so he adds 0.1 L of syrup into each of the cups. What is the final amount of juice in each cup?
A. 0.5 L
B. 0.7 L
C. 1.7 L
D. 2.0 L
Answer: b
DOK: Level 2
Source: Test Prep: MCA III Test Preparation Grade 7, Houghton Mifflin Harcourt Publishing Company, Attn: Contracts, Copyrights, and Licensing, 9400 South Park Center Loop, Orlando, FL 32819.
5.

Answer: b
DOK: Level 2
Source: Minnesota Grade 7 Mathematics MCA-III Item Sampler Item, 2011, Benchmark 7.1.2.5
6.

Answer: b
DOK: Level 2
Source: Minnesota Grade 7 Mathematics Modified MCA-III Item Sampler Item, 2011, Benchmark 7.1.2.5
7.
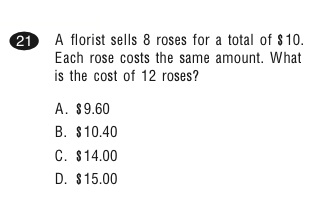
Answer: d
DOK: Level 2
Source: Massachusetts Comprehensive Assessment System Release of Spring 2010 Test Items
8.

Answer: b
DOK: Level 2
Source: Massachusetts Comprehensive Assessment System Release of Spring 2010 Test Items
Differentiation
- Provide students with multiplication tables.
- Students may need to be given a place value chart to help them in rounding to the correct place (hundreds vs. hundredths).
- Use pictures and or tables to help the students see the pattern; always label the values they are trying to scale, such as 10 in = 3 ft, 3 in = ________ft. By keeping the labels with the numbers, fewer errors in relationships will be made.
- Students may need to be given a place value chart to help them in rounding to the correct place (hundreds vs. hundredths).
- Students may see the word "ratio" as "radios." Assist them by clarifying the meaning and pronunciation of both words.
- Use a graphic organizer displaying operations with integer rules.
- Introduce √ of a number to plot on a number line.
- Do multi-step conversion-type problems to show proportional relationship.
- Explain the concept of compound interest using exponential growth and exponential equations.
- Create a gameboard activity. Have students work in groups of four to create gameboards marked with mathematical questions they must answer to be able to move ahead on the boards. They should use at least three addition, three subtraction, three multiplication and three division operations. They should also use positive numbers, negative numbers, decimals, and fractions. Students will fill in operation symbols and numbers on the boards. When they are done, the class can play the different games.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: (descriptive list) |
Teachers are: (descriptive list) |
|
finding the percent sign on a calculator. |
providing several different types of calculators to show the differences in the place value each calculator displays. |
|
rounding to correct place value. |
making tables of values to help introduce the concept of proportionality in these situations. |
|
converting percents to decimals, decimals to percents, and decimals to fractions, etc. |
using real-world contexts that the students are familiar with: recipes, scores in games, numbers of girls/boys in a class, etc. |
|
making tables of values to find patterns. |
making sure students are not just memorizing an algorithm for solving proportions when solving these types of problems. |
|
finding a percent of a number using multiple methods. |
exposing students to the difference between simple and compound interest. |
|
scaling values up and down correctly. |
|
|
using the context of the problem to make sense of it and perhaps drawing diagrams of the problem situation. |
|
|
using real-world examples to solve problems. |
|
|
relating proportions to everyday situations. |
|
