6.3.3 Converting & Estimating Measurements
Solve problems in various contexts involving conversion of weights, capacities, geometric measurements and times within measurement systems using appropriate units.
Estimate weights, capacities and geometric measurements using benchmarks in measurement systems with appropriate units.
For example: Estimate the height of a house by comparing to a 6-foot man standing nearby.
Overview
Big Ideas and Essential Understandings
Standard 6.3.3 Essential Understandings
Students have years of diverse experiences with measurement from prior classroom instruction and from using measurement in their everyday lives. These formal and informal experiences become the building blocks for students to estimate measurements and choose appropriate size and units of measurement for various situations.
Understanding the relationships among units within a measurement system is essential for students to use ratios to convert from one unit to another in solving problems. Students at this level use ratio and reasoning about multiplication and division to convert units within measurement systems and solve real-world and mathematical problems. This standard starts the learning progression of algebra concepts that moves students from ratios to proportions to functions, as well as the use of algebra in geometry.
6.3.3 Converting and Estimating Measurements
6.3.3.1 Solve problems in various contexts involving conversion of weights, capacities, geometric measurements and times within measurement systems using appropriate units.
6.3.3.2 Estimate weights, capacities and geometric measurements using benchmarks in measurement systems with appropriate units.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Know what is meant by length, capacity and weight;
- Select appropriate size and type of unit for a given measurement situation;
- Understand the size of each benchmark unit and the relationship among benchmark units within a measurement system;
- Identify equivalent ratios within a measurement system;
- Construct and analyze tables to show quantities that are in equivalent ratios;
- Use ratios and reasoning about multiplication and division to solve problems that require conversion of measurement units within a measurement system;
- Use common benchmarks to make reasonable estimates of measurements;
- Recognize new equivalences, such as 1 square yard equals 9 square feet and 1 cubic meter equals 1,000,000 cubic centimeters;
- Know useful approximate equivalents between the customary and metric systems, such as a quart is a little less than a liter, and a yard is a little less than a meter.
Work from previous grades that supports this new learning includes:
- Recognize and generate equivalent decimals, fractions, mixed numbers and improper fractions in various contexts;
- Solve real-world and mathematical problems requiring addition, subtraction, multiplication and division of multi-digit whole numbers. Use various strategies, including the inverse relationships between operations, the use of technology, and the context of the problem to assess the reasonableness of results;
- Create and use rules, tables, spreadsheets and graphs to describe patterns of change and solve problems;
- Represent real-world situations using equations and inequalities involving variables.
NCTM Standards
- Understand measurable attributes of objects and the units, systems, and processes of measurement:
- Understand both metric and customary systems of measurement;
- Understand relationships among units and convert from one unit to another within the same system;
- Understand, select, and use units of appropriate size and type to measure angles, perimeter, area, surface area, and volume.
- Apply appropriate techniques, tools, and formulas to determine measurements:
- Use common benchmarks to select appropriate methods for estimating measurements;
- Select and apply techniques and tools to accurately find length, area, volume, and angle measures to appropriate levels of precision;
- Solve problems involving scale factors, using ratio and proportion.
Common Core State Standards (CCSS)
- 5MD (Measurement & Data) Convert measurement units within a given measurement system.
- 5MD.1. Convert among different-sized standard measurement units within a given measurement system (e.g., convert 5 cm to 0.05 m), and use these conversions in solving multi-step, real world problems.
- 6RP (Ratio & Proportional Relationships) Understand ratio concepts and use ratio reasoning to solve problems.
- 6RP.3. Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios.
- 6RP.3.d. Use rate reasoning to convert measurement units; manipulate and transform units appropriately when multiplying and dividing quantities.
Misconceptions
- Students may multiply when converting to larger units and divide when converting to smaller units.
- Students may not know the prefixes used in the metric system or their meanings.
- Students may not be able to form mental pictures of measurement units, especially metric units, making it difficult for them to choose appropriate units or make reasonable estimates.
Vignette
Ms. Rykken's students were excited about the recent CO2 car competition in their industrial technology class, where they raced the cars they had designed and built. She decides to use this opportunity for them to use their own data and to review working with rates and unit conversion.

She began the class by asking for the velocity of the winning car. Students could only respond with the winning time (0.971 seconds).
Teacher: How is the velocity of real cars expressed?
Student: Speedometers tell us how many miles per hour we're going.
Teacher: That sounds like a relationship between distance and time. What is the relationship between distance and time for the winning CO2 car?
Student: Well, the track was 66 feet long and it took the car 0.971 seconds to travel that distance.
Teacher: So the winning car traveled 66 feet in 0.971 seconds. We can write that relationship as a ratio, or fraction $\frac{66\ feet}{0.971\ seconds}$ . But you said that real cars express velocity as miles per hour. How can we convert feet per second to miles per hour?
Student: The feet need to be changed to miles, and the seconds need to be changed to hours.
Teacher: Yes, but how do we do that?
Student: I know how to change the time. There are 60 seconds in every minute, and 60 minutes in every hour. We can just multiply.
Teacher: Tell me more.
Student: If I multiply $\frac{66\ feet}{0.971\ seconds}\times \frac{60\ seconds}{1\ minute}\times \frac{60\ minutes}{1\ hour}$, I'll know how many feet the car went in 1 hour.
Teacher: How do we know that multiplying by those fractions didn't change the original velocity?
Student: Because each of the fractions is equivalent to 1, and multiplying by 1 gives you the same value.
Teacher: Since the fractions are equivalent to 1, could I have inverted them and gotten the same result from multiplying?
Student: No, that would mess up the units. The fractions need to be set up so that the units cancel, like seconds with seconds and minutes with minutes. After multiplying, you're left with $\frac{237,600\ feet}{0.971\ hour}$.
Teacher: That makes sense. Now we've converted the time, but we're not finished. For real cars, we express velocity in miles per hour. How do we convert the feet to miles?
Student: The same way. We multiply using the relationship that every mile has 5,280 feet.
Teacher: Do I multiply by $\frac{5,280\ feet}{1\ mile}$ or $\frac{1\ mile}{5,280\ feet}$?
Student: If you want the feet to cancel, you'll need to use $\frac{1\ mile}{5,280\ feet}$ .
Teacher: Like this? $\frac{237,600\ feet}{0.971\ hour}\times \frac{1\ mile}{5,280\ feet}$?
Student: Yes.
Teacher: What is the result?
Student: About 46.3 miles per hour.
Teacher: WOW! That's amazing! It's a good think you didn't race your cars outside the school, because the speed limit there is 30 miles per hour.
Student: Could we have changed the feet to miles first and gotten the same answer?
Teacher: Good question. Does it change the result if we multiply in a different order?
Student: No, multiplication is commutative, which means that the order doesn't matter.
Teacher: Yes, that's right.
Student: I did all those steps at the same time and got the same result.
Teacher: Like this: $\frac{66\ feet}{0.971\ seconds}\times \frac{60\ seconds}{1\ minute}\times \frac{60\ minutes}{1\ hour}\times\frac{1\ mile}{5,280\ feet} $? Excellent! That's very efficient. Now I'd like each of you to find the velocity of your CO2 car in miles per hour.
Ms. Rykken circulates the room to assist students and hear tales of their race experiences.
Resources
Teacher Notes
- Students incorrectly multiply when converting to larger units and divide when converting to smaller units when they do not recognize that the size of the unit and the number of units needed to measure an object are inversely related; as one increases, the other decreases. Understanding this relationship is essential for students to be able to make reasonable estimates. Students can develop this understanding by using familiar contexts. For example, students will understand that exchanging five dollars for pennies will result in more than five pennies, since you're moving to a smaller unit. Similarly, converting 50 inches into feet will result in fewer feet since you're moving to a larger unit.
- Students may find the acronym "King (kilo) Henry(hecto) Died (deka) Drinking (deci) Chocolate (centi) Milk (milli)" helpful to remember the order of commonly used metric prefixes. Making explicit connections to place value and the fact that next-smaller and next-larger units differ by a power of 10 will support students in understanding the relationship between units.
- Students need multiple hands-on experiences in measuring in order to understand the size of various units, form mental pictures, and make reasonable estimates.
- Students will benefit from teacher use of multiple approaches to converting units within a measurement system. Creating tables is especially helpful for students to see equivalent ratios and use reasoning about multiplication and division when making unit conversions. By viewing equivalent ratios and rates as deriving from and extending pairs of rows (or columns) in multiplication tables, students connect their understanding of multiplication and division with ratios and rates.
- Students need to understand that they're actually multiplying by one when using unit analysis to make conversions. Reminding them that the goal is to "cancel" the old units, similar to "canceling" common factors when simplifying fractions, will help them decide how to write the ratio used for conversion ($\frac{1\ yard}{3\ feet}$ or $\frac{3\ feet}{1\ yard}$).
- Although students are more familiar with the customary measurement system, this system can be especially challenging as the relationships between units are cumbersome and require an understanding of fractions. Measurement in the customary system provides an opportunity for students use fractions in real-world situations.
Weighing Your Car
This lesson asks students to measure the area of a car tire's footprint and its air pressure in order to estimate the car's weight.
Have You Ever Seen a Tree Big Enough to Drive a Car Through?
This challenge allows students explore how foresters use measurement.

Information |Description= Henry Cowell Redwoods State Park, Redwood Grove. Man standing beside a particularly large Coastal Redwood tree. |Source= Created this image on Honeymoon in Santa Cruz, CA |Date= October, 2006 |Author= Larry McElhiney |Permiss)
Does Polygon Need a Jacket?
This challenge asks students to estimate the temperature in Fahrenheit given Celsius.
Additional Instructional Resources
Learning Measurement Through Practice
This article describes a team-taught activity-based format to teach students about measurement.
New Vocabulary
capacity: measure of how much a container can hold. Units of capacity are special types of volume units used for containers whose length, width, and height cannot be measured. Capacity is usually used for things such as liquids or pourable substances, such as grains of sugar.
Example: The capacity of a soda pop can is 12 fluid ounces or 355 milliliters.
customary system: measurement system used most often in the United States.
Examples:
length: inch, foot, yard, and mile
weight: ounce, pound, and ton
capacity: cup, pint, quart, and gallon
temperature: degrees Fahrenheit
metric system: measurement system used in most countries around the world based on the base-ten numeration system.
Examples:
length: millimeter, centimeter, meter, and kilometer
weight: gram and kilogram
capacity: milliliter and liter
temperature: degrees Celsius
metric system prefixes: kilo means 1000, hecto means 100, deka means 10, deci means $\frac{1}{10}$, centi means $\frac{1}{100}$, and milli means $\frac{1}{1000}$.
weight: measure of how heavy something is.
Example: The weight of a bag of sugar may be 4 pounds or 1.8 kilograms.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- How were multiple approaches and strategies modeled for solving problems that required converting measurement units?
- How was measurement connected to other areas of mathematics?
- How was measurement connected to other content areas?
- How were measurement concepts and skills used to solve real-world problems?
- What strategies were used to develop a sense of reasonableness when measuring?
- Did students have frequent opportunities for hands-on measurement?
- How were important social and scientific contexts used to make measurement relevant to students' lives?
Materials
- NCTM: Principles and Standards for School Mathematics
- Grades 6-8 Measurement Standard for Grades 6-8 (pp. 240-247).
- NCTM: A Research Companion to Principles and Standards for School Mathematics
- Chapter 12, Developing Understanding of Measurement (p. 181).
- Keeley, P., & Rose, C. (2006). Mathematics curriculum topic study. Thousand Oaks, CA: Corwin Press.
- Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
- Mathematics Curriculum Framework. (2000). Malden, MA: Massachusetts Department of Education.
- Mathematics Framework for the 2009 National Assessment of Educational Progress. (2009). Washington, D.C.: National Assessment Governing Board, U.S. Department of Education.
- Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
- Developing essential understanding of ratios, proportions & proportional reasoning: Grades 6-8. (2010). Reston: VA: National Council of Teachers of Mathematics, Inc.
- Principles and standards for school mathematics. (2000). Reston, VA: National Council of Teachers of Mathematics, Inc.
Assessment
(DOK: Level 1)
1. Last week, Harry walked his dog 4 days at a nearby park. Each day they walked on a trail 2,400 meters long. How many kilometers did they walk at the park last week?
a. 9,600 kilometers b. 960 kilometers
c. 96 kilometers d. 9.6 kilometers

Answer: d
(DOK: Level 2)
2. The pilot of a passenger jet announced that their cruising altitude was approximately 31,750 feet. About how many miles above the ground is the plane? Explain your reasoning.

Answer: The plane is about 6 miles above the ground. There are 5,280 feet in one mile, so I divided 31,750 by 5,280 to find the number of miles in 31,750 feet. The answer is a little more than 6.
(DOK: Level 2)
3. A delivery truck brought several bags of concrete mix to a home improvement store. In all, 10.8 tons of concrete mix were delivered. If each bag of concrete mix weighed 60 pounds, about how many bags did the truck deliver?

a. 556 bags b. 360 bags
c. 270 bags d. 180 bags
Answer: b
(DOK: Level 3)
4. The perimeter of a rectangular garden is 0.72 km. The length of the garden is 160 meters. What is the width of the garden? 
Answer: 200 m or 0.2 km
(DOK: Level 3)
5. Figure out which number goes in which place, using reasonable estimates.
A man weighs _____ kg. This is _____ times the amount he weighed at birth.
He drives his car _____ miles in one hour. This is _____ times the distance he walks in one hour. 15 22 60 88

Possible answer: 88, 22, 60, 15
(DOK Level 4)
6. Mike uses a pedometer to keep track of how many steps he takes each day. He plans to hike 8 miles next Saturday. Predict how many steps Mike's pedometer will show from hiking 8 miles. Explain your reasoning.

Possible answer: Using the approximation $2\frac{1}{2}$ feet per step, Mike's pedometer would register about 16,900 steps. (8 x 5,280 ![]() 2.5 = 16, 896)
2.5 = 16, 896)
Differentiation
Struggling Learners
- Provide a graphic organizer showing units used for measuring length, capacity, and weight in measurement systems.
Example:
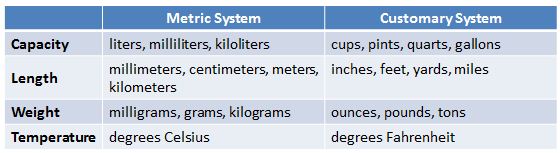
- Provide key benchmark relationships for measurement systems.
Examples:


- Post "rules of thumb" to help students develop a sense of reasonableness when converting between measurement systems.
Example:
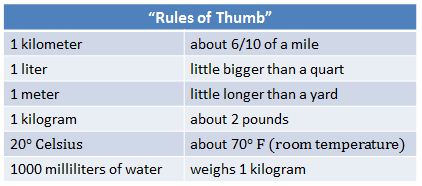
- To explore the concept of capacity, have students compare the capacity of five different-size containers. Ask students to predict which containers have the largest and smallest capacities. Then have students use fill material (macaroni, centimeter cubes) to compare the capacities of the five containers and to determine if their predictions were correct. Encourage students to continue to develop their personal references as they make and check their predictions.
- Students new to the United States will most likely be unfamiliar with the customary system. It is critical for them to have hands-on experiences measuring length, weight and capacity using both customary and metric units.
- Measure distances using rulers and tape measures that show both customary and metric units. Post pictures and maps showing distances labeled with appropriate customary and metric units.
- Label containers appropriately with cup, pint, quart, gallon, and liter, and use graduated cylinders and measuring cups to measure capacity. Post pictures of containers and their capacities. Ask students to find real-world examples that show capacity in both customary and metric units; e.g., a soda pop can contains 12 fluid ounces or 355 milliliters.
- Use scales and balances to measure weight. Label objects that weigh 1 ounce, 1 pound, 1 gram, and 1 kilogram. Post pictures of objects and their weight in both measurement system. Ask students to find real-world examples that show weight in both customary and metric units; e.g., a bag of sugar weighs 4 pounds or 1.8 kilograms.
- Post charts showing the relationships among benchmark units within a measurement system.
- Encourage students to look for the prefixes in number names when using the metric system. Consider having students illustrate some of the words and prefixes they discuss.
- Use graphic organizers, such as the Frayer model shown below, for vocabulary development.
- Can You Run as Fast as a Car?
This challenge requires students compare rates between customary and metric measurement systems.
- Converting Units of Length
The video on this site will help students convert between measurement systems.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) | Teachers are: (descriptive list) |
selecting reasonable units of measure, deciding on appropriate tools and measuring actual objects, including irregular shapes and objects. | using the real world as a source of opportunities for measurement investigations that require multiple decisions. |
using commonly understood benchmarks to estimate measurements, then testing their predictions for reasonableness when possible. | asking students to compare estimated and actual measurements to develop a sense of reasonableness. |
understanding that measurements are approximate and that units are chosen based on the degree of accuracy needed and tools available for measurement. | giving students experiences in judging what degree of accuracy is required in a given situation and whether an overestimate or underestimate is more desirable. |
generalizing measurement techniques and strategies to develop formulas. | providing experiences for exploration and discovery of formulas rather than providing formulas and asking for rote memorization; helping students recognize formulas as efficient ways to count repeated units. |
making connections between units of length, area and volume. | emphasizing how length and width are combine to form the square units of area; and how length, width, and height are combined to form the cubic units of volume. |
using ratios and reasoning strategies to solve problems involving conversion of units within measurement systems. | proposing problems that require students to use ratios and reasoning strategies in converting units within measurement systems. |
using approximate "rules of thumb" to convert units between measurement systems. | asking students to make approximations in the metric system based on customary measurement and vice-versa. |
connecting measurement to other mathematical areas. | explicitly connecting measurement to number, geometry, algebra and data analysis. |
connecting measurement to other content areas. | collaborating with colleagues to integrate content and support students in making connections. |
using measurement concepts and skills to solve real-world problems and extending their learning to new situations. | requiring a dynamic interaction between students and their environment, so that students encounter measurement outside of school, as well as inside. |
communicating mathematical thinking to others; analyzing others' mathematical thinking and strategies. | selecting students with different approaches to share thinking with the class. |
