6.3.2B Angles in Geometric Figures
Determine missing angle measures in a triangle using the fact that the sum of the interior angles of a triangle is 180˚. Use models of triangles to illustrate this fact.
For example: Cut a triangle out of paper, tear off the corners and rearrange these corners to form a straight line.
Another example: Recognize that the measures of the two acute angles in a right triangle sum to 90˚.
Develop and use formulas for the sums of the interior angles of polygons by decomposing them into triangles.
Overview
Standard 6.3.2 Essential Understandings
The focus of instruction at this level is to explore cause and effect relationships of angles in geometric figures. Relationships of complementary, supplementary, right, straight, adjacent and vertical angles formed by intersecting lines are used to solve problems. The relationship of the sum of the interior angles of a triangle is used to find missing angles in a triangle. This relationship is applied when students decompose other polygons into triangles to develop and use formulas for sums of their interior angles. While geometry is the focus, there are other connections occurring. The process of students developing understanding of these relationships and formula is a direct result of purposeful application of Algebraic Habits of Mind. Engaging students in doing and undoing, abstracting from numbers, and building rules are essential components of this learning process.
Benchmark Group B - Angles of triangles and other polygons
6.3.2.2 Determine missing angle measures in a triangle using the fact that the sum of the interior angles of a triangle is 180o. Use models of triangles to illustrate this fact.
6.3.2.3 Develop and use formulas for the sums of the interior angles of polygons by decomposing them into triangles.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Know that the sum of the interior angles of any triangle is 180o;
- Find missing angle measures in triangles using the fact that the sum of the interior angles of any triangle is 180o;
- Decompose polygons into triangles;
- Find sums of interior angles of polygons by decomposing them into triangles and using the fact the sum of the interior angles of any triangle is 180o;
- Develop and use a formula to find sums of interior angles of polygons.
Work from previous grades that supports this new learning includes:
- Measure angles in geometric figures and real-world objects with a protractor or angle ruler;
- Solve real-world and mathematical problems requiring addition and subtraction of decimals, fractions and mixed numbers, including those involving measurement, geometry and data;
- Describe, classify and sketch triangles, including equilateral, right, obtuse and acute triangles;
- Recognize triangles in various contexts.
Misconceptions
- Students may misread a protractor.
- Students may have difficulty decomposing polygons into triangles.
- Students may struggle to develop the formula to find sums of interior angles of polygons.
Vignette
In this vignette, Mr. Gonzalez wanted his students to discover that the sum of the interior angles of any triangle is 180º. In preparation for this lesson, he asked students to draw and cut out one example each of an equilateral triangle, an acute triangle, a right triangle and an obtuse triangle, as homework before class began. Sides needed to be cut very straight, and angles were to be named and measured.
Mr. Gonzalez: Good morning. I see that many of you already have your triangles out on your desk and are ready to begin today's lesson. Thanks for being prepared and ready to go. If you haven't already done so, please take out your triangles.
Student: I forgot to do my homework.
Mr. Gonzalez: For now, I'd like you work with your partner and use her triangle for this investigation. Then tonight, you can make your own triangle and use it to repeat the investigation.
Student: You mean I still have to do the assignment?
Mr. Gonzalez: Yes, that's exactly what I mean. Has everyone named and measured all angles in each of their four triangles?
Student: I wrote the angle measurements in my notebook, but some people wrote them write on the triangle. Does that matter?
Mr. Gonzalez: No, the important thing for this investigation is that you know the measurement of each angle. Other questions?
Student: Yes. I only made three triangles, because I counted my equilateral triangle as an example of an acute triangle.
Student: That's not fair! You mean I wouldn't have had to make a fourth triangle?
Mr. Gonzalez: Let's talk about this. What are the characteristics of an equilateral triangle?
Student: All three sides and all three angles are congruent.
Mr. Gonzalez: And what is the measure of each of those congruent angles?
Student: 60º. Actually I got 59º, 60º and 61º when I measured the angles of my triangle, but that's because I was a little off in my measurements.
Mr. Gonzalez: Yes, each of the angles of an equilateral triangle does measure 60º, and that's a good observation about the accuracy of your measurements. Now what do we know mean when we classify a triangle as acute?
Student: Well that means that all three angles of the triangle are acute angles, so each of the angles is less than 90º.
Mr. Gonzalez: So can an equilateral triangle be considered an acute triangle?
Student: I suppose, but then most of us spent more time making triangles than we needed to.
Mr. Gonzalez: Your extra time will provide us with more triangles to use in our investigation today. Thanks for spending the extra time! If there are no other questions, let's get started. As you know, triangles can be classified by the measure of their angles. Today you have brought examples of every possible triangle that can be made using those classifications. We have acute triangles - some equilateral and some not - as well as right and obtuse triangles. Although each of your triangles may be a different shape or size, I think we are going to discover all of your triangles share a special relationship. Let's begin by making a table to show the data you collected. In the table, I'd like you to include the type of triangle (acute, right, obtuse, or equilateral), the measure of each angle in the triangle, and the sum of the angles in each triangle.
Student: You mean you want us to add up the angles?
Mr. Gonzalez: Yes, I want you to find the sum. You may record your data in your notebooks. Go ahead and get started.
(Mr. Gonzalez circulates the room assisting students.)
Mr. Gonzalez: Now that you've finished making your table, I'd like you to turn to your partner and share your data. Look for patterns in the data. Remember that we're looking for a special relationship that all of your triangles share. Let's see if you can discover that relationship.
(Students discuss data.)
Sample student data:
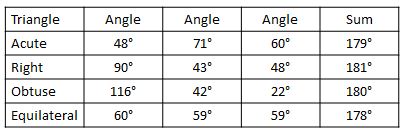
Mr. Gonzalez: All right. I've heard lots of good discussion about what the special relationship that all triangles share might be. Let's start by talking about what patterns you saw in your data.
Student: I noticed that the sum for everybody's triangle was somewhere around 180º.
Mr. Gonzalez: Does others agree with that? (Heads nod.) What conclusions can you draw from that observation?
Student: I think that the sum of the angles for any triangle is supposed to be 180º.
Mr. Gonzalez: How many of you agree with that statement? (All hands are raised.) Then here's a question for you. If that's true, why didn't you always get 180º for the sum of the angles?
Student: Because measurement is always approximate. There's no such thing as a perfect measurement.
Mr. Gonzalez: I certainly agree that there's room for error in measurement. So I hear you saying that you think the special relationship that every triangle shares is that the sum of the angles is 180º. Who can tell me what the name is for an angle that measures 180º?
Student: It's a straight line.
Mr. Gonzalez: Yes, a 180º angle is called a straight angle and forms a straight line. If the sum of the angles of any triangle is 180º, then we should be able to use the angles to make a straight line. Right now I'd like each of you to choose one of your triangles, rip off the corners, and see if you can put the angles together to form a straight line. Let me show you what I mean. Who's willing to let me use one of your triangles to demonstrate?
Sample of student work:

Mr. Gonzalez: Tomorrow we'll use the fact that the sum of the angles for every triangle is 180º to see if we can predict the sum of the angles for a quadrilateral, pentagon, hexagon, or any polygon.
Student: Is our homework to bring you examples of different polygons?
Mr. Gonzalez: Good idea, but you have the night off. See you tomorrow!
Resources
Teacher Notes
- Providing experiences in determining and using benchmark angles will help students correctly read a protractor. Estimating that an angle is less than 90º should prevent a student from misreading a measurement of 150º for a 30º angle. Students can develop a repertoire of benchmark angles, including right angles, straight angles and 45º angles. They should be able to offer reasonable estimates for the measurement of any angle between 0º and 180º. Checking the reasonableness of a measurement should be a part of the process.
- One strategy to help students decompose polygons into triangles is to start with one vertex and connect it to all the other vertices, and then rotate clockwise to the next vertex and repeat the process. As students decompose polygons into triangles, emphasize that the sides of the triangles must be diagonals and cannot intersect.
- For students to develop the formula for the sum of the interior angles of an n-gon, they need to be engaged in investigations that allow them to observe the pattern of the sum of the interior angles of a polygon, increasing by 180 as the number of sides increases by one. The use of a table for data collection, such as the one shown below, will help in the discovery of this relationship.

Possible ways to represent the relationship between the number of sides and the angle sum include S = 180n - 360 and S = 180(n - 2).
Students explore the angles in various polygons and find a relationship between the number of sides and the sum of the interior angles.
Students draw various polygons and investigate their interior angles. The lesson concludes with students developing a formula to show the relationship between the number of sides of a polygon and the sum of the interior angles.
Additional Instructional Resources
This site includes a link to an interactive Sketchpad demonstration
New Vocabulary
diagonal: line segment joining two non-adjacent vertices of a polygon.
Example:

Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- How were students supported to discover cause and effect relationships in geometric figures?
- What opportunities were provided for students to communicate their thinking and ideas?
- How were Algebraic Habits of Mind (e.g., doing and undoing, abstracting from numbers and building rules) encouraged?
- Keeley, P., & Rose, C. (2006). Mathematics Curriculum Topic Study. Thousand Oaks, CA: Corwin Press.
- Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A Research Companion to Principles and Standards for School Mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
- Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
- National Council of Teachers of Mathematics. (2000). Principles and Standards for School Mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
- Wyatt, K., Lawrence, A., & Foletta, G. (2004). Geometry Activities for Middle School Students. Emeryville, CA: Key Curriculum Press.
Assessment
(DOK: Level 1)
1. Use the formula S = 180 (n - 2), where S represents the sum of the interior angle measures and n represents the number of sides of a polygon, to find the sum of the angle measures of a polygon with 12 sides.
Answer: 1800°
(DOK: Level 1)
2. Solve for x.
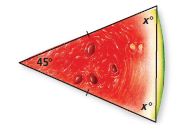
Answer: x = 67.5
(DOK: Level 2)
3. What is the measure of angle A?
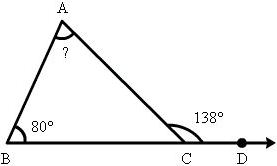
a. 42° b. 50° c. 58° d. 100°
Answer: c
(DOK: Level 3)
4. Each angle measures 140º in a polygon with angles are of equal measure. How many sides does the polygon have?
a) 7 b) 8 c) 9 d) 10
Answer: c
(DOK: Level 4)
5. The diagram shows a regular octagon. Beth drew diagonals from vertex A to all other non-adjacent vertices. What is the measure of ∠HAF?
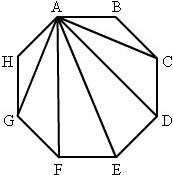
Answer: 45o
Differentiation
Struggling Learners
- Post pictures of polygons with diagonals drawn to show how they can be decomposed into triangles.
- Provide tables during investigations to record the number of sides of polygons and the sums of the interior angles of polygons.
- Ask questions that lead students to observe patterns when developing the formula for the sums of interior angles of polygons.
- Have students use calculators to assist with computation.
- Post and label pictures of polygons, such as quadrilaterals, pentagons, hexagons, etc.
- Post pictures with diagonals drawn and labeled showing how polygons can be decomposed into triangles;
- Use graphic organizers, such as the Frayer model shown below, for vocabulary development.

- Have students explore exterior angles of polygons. The sum of the exterior angles for any polygon is 360o. Therefore the measure of one exterior angle of a regular polygon is 360/n.
This site challenges students to construct a cube from ten tetrahedral pieces.
This activity proves that the sum of the angles of any triangle is 180o, using a concrete model and algebraically. This fact is used to algebraically solve triangle problems with missing angles.
This site challenges students to use angle relationships to find missing angles. An instructional video includes the solutions.
In this lesson, students explore regular and semi-regular tessellations.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) | Teachers are: (descriptive list) |
measuring angles of various triangles to discover the angle sum relationship. | providing hands-on opportunities for students to measure angles and discover the angle sum relationship. |
using models of triangles to illustrate the angle sum relationship. | asking students to demonstrate the angle sum relationship. |
drawing diagonals to decompose various polygons into triangles. | modeling the decomposition of polygons into triangles. |
observing the relationship between the number of sides and the sum of the interior angles of polygons. | posing questions that lead students to develop formulas for the sums of interior angles of polygons. |
using formulas to find the sums of interior angles of polygons. | asking students to use formulas to find sums of interior angles of polygons and solve related problems. |
using variables to represent unknown quantities and solve problems involving angle relationships in geometric figures. | modeling the use of algebra to solve problems involving angle relationships in geometric figures. |
discussing and writing about cause and effect relationships of angles formed by intersecting lines using precise mathematical language. | providing opportunities for students to communicate their thinking and ideas. |
