6.3.1 Measurement of Polygons & Prisms
Calculate the surface area and volume of prisms and use appropriate units, such as cm2 and cm3. Justify the formulas used. Justification may involve decomposition, nets or other models.
For example: The surface area of a triangular prism can be found by decomposing the surface into two triangles and three rectangles.
Calculate the area of quadrilaterals. Quadrilaterals include squares, rectangles, rhombuses, parallelograms, trapezoids and kites. When formulas are used, be able to explain why they are valid.
For example: The area of a kite is one-half the product of the lengths of the diagonals, and this can be justified by decomposing the kite into two triangles.
Estimate the perimeter and area of irregular figures on a grid when they cannot be decomposed into common figures and use correct units, such as cm and cm2.
Overview
Standard 6.3.1 Essential Understandings
Students bring to the middle grades many years of diverse experiences with measurement from prior classroom instruction and using measurement in their everyday lives. These formal and informal experiences with measurable attributes are used as building blocks in developing strategies to calculate area of quadrilaterals, including parallelograms, rhombuses, trapezoids, and kites. Area formulas are developed and when used, can be justified. Students also estimate perimeter and area of irregular figures on a grid that cannot be decomposed into common figures.
Measurement experiences with two-dimensional figures are extended and connected to three-dimensional figures. Strategies are developed to determine surface area and volume of three-dimensional figures, using appropriate units. Formulas for surface area and volume are developed and when used, justified. Measurement data is recorded in tables so that patterns can be observed. These concepts and skills connect ideas of number and operation, algebra, geometry and measurement, and data analysis.
All Standard Benchmarks
6.3.1.1 Calculate the surface area and volume of prisms and use appropriate units, such as cm2 and cm3. Justify the formulas used. Justification may involve decomposition, nets or other models.
6.3.1.2. Calculate the area of quadrilaterals. Quadrilaterals include squares, rectangles, rhombuses, parallelograms, trapezoids and kites. When formulas are used, be able to explain why they are valid.
6.3.1.3 Estimate the perimeter and area of irregular figures on a grid when they cannot be decomposed into common figures and use correct units, such as cm and cm2.
6.3.1.1 Calculate the surface area and volume of prisms and use appropriate units, such as cm2 and cm3. Justify the formulas used. Justification may involve decomposition, nets or other models.
6.3.1.2. Calculate the area of quadrilaterals. Quadrilaterals include squares, rectangles, rhombuses, parallelograms, trapezoids and kites. When formulas are used, be able to explain why they are valid.
6.3.1.3 Estimate the perimeter and area of irregular figures on a grid when they cannot be decomposed into common figures and use correct units, such as cm and cm2.
What students should know and be able to do [at a mastery level] related to these benchmarks.
- Find areas of squares, rectangles, rhombuses, parallelograms, trapezoids, and kites, including the use of formulas;
- Justify why formulas for areas of squares, rectangles, parallelograms, triangles, and trapezoids are valid;
- Estimate perimeter and area of irregular figures on a grid and use appropriate units;
- Distinguish between the concepts of surface area and volume;
- Calculate surface area and volume of prisms using appropriate units;
- Use two-dimensional representations of three-dimensional figures to visualize and solve problems involving surface area and volume;
- Use nets to analyze figures, then calculate surface area and volume;
- Develop an understanding of formulas used to determine surface areas and volumes of three-dimensional figures;
- Use formulas to determine surface area and volume;
- Justify formulas for surface area and volume using nets, decomposition, or other models;
- Find lengths from areas or volumes;
- Solve simple equations involving formulas by using number sense, properties of operations, and the idea of maintaining equality on both sides of an equation.
Work from previous grades that supports this new learning includes:
- Describe and classify three-dimensional figures including cubes, prisms and pyramids by the number of edges, faces or vertices as well as the types of faces;
- Recognize and draw a net for a three-dimensional figure;
- Understand that the area of a two-dimensional figure can be found by counting the total number of same size square units that cover a shape without gaps or overlaps. Justify why length and width are multiplied to find the area of a rectangle by breaking the rectangle into one unit by one unit squares and viewing these as grouped into rows and columns;
- Develop and use formulas to determine the area of triangles, parallelograms and figures that can be decomposed into triangles;
- Determine the surface area of a rectangular prism by using various strategies;
- Understand that the volume of a three-dimensional figure can be found by counting the total number of same-size cubic units that fill a shape without gaps or overlaps. Use cubic units to label volume measurements;
- Develop and use the formulas V=lwh and V=Bh to determine the volume of rectangular prisms. Justify why base area B and height h are multiplied to find the volume of a rectangular prism by breaking the prism into layers of unit cubes;
- Use various tools to measure the volume and surface area of various objects that are shaped like rectangular prisms;
- Understand that a variable can be used to represent a quantity that can change, often in relationship to another changing quantity. Use variables in various contexts.
NCTM Standards
Apply appropriate techniques, tools, and formulas to determine measurements:
- Develop and use formulas to determine the area of triangles, parallelograms, and trapezoids, and develop strategies to find the area of more-complex shapes;
- Develop strategies to determine the surface area and volume of selected prisms and pyramids;
- Select and apply techniques and tools to accurately find length, area, volume, and angle measures to appropriate levels of precision.
Understand measurable attributes of objects and the units, systems, and processes of measurement:
- Understand both metric and customary systems of measurement;
- Understand, select, and use units of appropriate size and type to measure perimeter, area, surface area, and volume.
Apply appropriate techniques, tools, and formulas to determine measurements:
- Develop and use formulas to determine the area of triangles, parallelograms, trapezoids and develop strategies to find the area of more complex shapes;
- Develop strategies to determine the surface area and volume of selected prisms;
- Select and apply techniques to accurately find length and area to appropriate levels of precision.
Apply and adapt a variety of appropriate strategies to solve problems.
Recognize reasoning and proof as fundamental aspects of mathematics.
Organize and consolidate their mathematical thinking through communication.
Communicate their mathematical thinking coherently and clearly to peers, teachers, and others.
Use the language of mathematics to express mathematical ideas precisely.
Common Core State Standards (CCSS)
6.G (Geometry) Solve real-world and mathematical problems involving area, surface area, and volume.
- 6.G.1. Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world mathematical problems.
- 6.G.2 Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism. Apply the formulas V=lwh and V=bh to find the volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.
7.G. (Geometry) Solve real-life and mathematical problems involving angle measure, area, surface area, and volume.
- 7.G.6. Solve real-world and mathematical problems involving area, volume, and surface area of two-dimensional and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Misconceptions
Student Misconceptions and Common Errors
- Students may have difficulty distinguishing the concepts of perimeter, area, and volume, resulting in the choice of inappropriate units;
- Students may know area and volume formulas, but are not able to link those formulas to the idea of covering a shape with same-size square units or filling a space with same-size cubic units without gaps or overlaps;
- Students may have difficulty visualizing the unseen faces of a three-dimensional figure, making it difficult to find the surface area;
- Students may have difficulty visualizing volume for closed containers;
- Students may be confused about why square units are also used to measure area and cubic units to measure volume, especially when the shapes or objects being measured are not squares or cubes;
- Students may believe that if the volume of a three-dimensional figure is known, then its surface area can be determined.
Vignette
In the Classroom
Mr. Lee's class has been exploring the relationship between surface area and volume. He's concerned that some students have the misconception that surface area can always be determined given the volume. He also wants students to observe patterns in the tables they construct for different fixed volumes and note that prisms that are cube-like (i.e., whose dimensions are nearly equal) tend to have less surface area than those that are less cube-like.
Teacher: On your desk are 12 stacking cubes. I'd like you to work with your partner to build as many rectangular prisms as you can using all 12 cubes. Be sure to record the dimensions of your prisms, as well as the volume and surface area for each prism on the data table provided.
Sample student work:
Student: Mr. Lee, is a rectangular prism that's 2 cubes wide, 3 cubes long, and 2 cubes high the same as a rectangular prism that's 2 cubes wide, 2 cubes long, and 3 cubes high?
Teacher: Does anyone have thoughts about that?
Student: Well, you can rotate one to look just like the other. I don't think it matters which dimension is the length, or width, or height. The prisms are identical.
Teacher: Yes, the prisms are identical. Let's agree that we're only going to record the dimensions of identical prisms once.
Student: Won't all of our rectangular prisms have the same volume?
Teacher: What makes you think that?
Student: Because each one uses 12 cubes, so the volume for each prism is 12.
Teacher: Good observation. Since volume is the number of cubes that fill a space, it makes sense that each of the rectangular prisms has a volume of 12.
Sidebar: Note the concept of congruence, even though the term is not used.
Student: How many prisms are we supposed to be able to make? I've got two already.
Teacher: Tell me how. What strategy are you using to organize your thinking?
Student: I really don't have a strategy. I'm just trying different numbers to see if I can use up all the cubes.
Student: I think there are four different prisms that can be made.
Teacher: It sounds like you're pretty confident about that. How do you know?
Student: First I made every possible prism that was one cube high. There were three possibilities: 1 x 1 x 12, 1 x 2 x 6 and 1 x 3 x 4. Then I tried to make all possible prisms that were two cubes high. One of those possibilities was already listed - the 1 x 2 x 6. The only new possibility was 2 x 2 x 3. Then I tried all possible ways to make a prism three cubes high. There were only two ways to make them, and I had already written them down. Then I tried four cubes high, five cubes high, and so on, but didn't find any more possibilities.
Sidebar: The student's method for listing systemically is very similar to alphabetizing.
Teacher: What was the highest prism you tried to build?
Student: I quit when I got to six, because I knew that 6x2 would use all the cubes and I couldn't go any higher.
Teacher: Good reasoning! Does anyone else have comments to add?
Student: So you found four different prisms. How did you find the surface area for them?
Student: My partner and I counted the squares on each of the faces and added up all those numbers.
Teacher: Surface area is the number of squares that it takes to cover the faces, or surface, so that strategy certainly can be used.
Student: I found surface area another way. Since each face is a rectangle, I multiplied the length times the width and then added the areas of the six faces.
Teacher: So you used the formula for area of a rectangle to find the area of each face, and then added those results?
Student: Yeah, but it takes a long time to do that for each prism. That's six different area problems.
Teacher: Good point. Is there another way to find surface area that might be more efficient?
Student: My partner and I used the formula for area of a rectangle, but we only found the area of three faces, added them together, and then doubled it. We got the same answer
Sidebar: Note the use of the distributive property (adding first, then doubling).
Teacher: Why do you think you got the same answer?
Student: You should get the same answer because the top and bottom are the same size, the front and back are the same size, and the two sides are the same size. If you add the areas of the top, front, and back, and then multiply by two, that's the same as adding all six parts together.
Teacher: Let's take a minute to review the data we've collected so far. Do you see any patterns?
Student: All the prisms have the same volume, but they have different surface areas.
Teacher: Does everyone agree with that statement?
Students nod heads in agreement.
Teacher: Any other observations you made?
Student: Yes, the long, skinny prism has the biggest surface area. As the prisms get fatter, the surface area goes down.
Sidebar: The "fat-skinny" discussion also applies for two-dimensional figures and should not be ignored.
Teacher: Interesting observation. Does everyone understand what he means by "fatter?" I think he's trying to say that the dimensions are getting closer to the same size. The prism is becoming shaped more like a cube. Let's try this same activity again, this time using 24 cubes. I'll be coming around to your desks to give you 12 more cubes. Please record the dimensions, volume, and surface area on the same table you used with your last data. Think about what strategies you could use to complete this task more efficiently than the last time. If you finish early, review your data and look for patterns.
Mr. Lee circulates around the room assisting students.
Teacher: What did you learn when you had 24 cubes available for building rectangular prisms?
Student: Just like last time, all prisms had the same volume, 24.
Teacher: Yes. And what would you expect if I gave you 50 cubes?
Student: Their volume would be 50.
Teacher: 83 cubes?
Student: Volume would be 83.
Teacher: I think you have the concept that volume is the number of cubes. What did you notice about the number of prisms that could be built?
Student: We found more prisms - 6 this time, and I think we got them all because we started by finding all prisms that were one cube high, then two cubes, and so on.
Teacher: Do others agree that there are 6 possible rectangular prisms that can be built with 24 cubes?
Student: Yes, and each of them has a different surface area.
Teacher: So if I told you that a rectangular prism had a volume of 75 cubic units, would you be able to predict its surface area?
Student: No. If a prism with a volume of 24 cubes has 6 different possible surface areas, I bet that a volume of 100 cubes would probably have even more. There's no way you could predict the surface area without knowing more information.
Teacher: What else did you notice about the data in your table?
Student: The dimensions are all factors of the volume.
Teacher: Yes, they can be multiplied together to find the volume. That helps you understand why the formula for finding the volume of a rectangular prism is l x w x h. Any other observations?
Student: In both cases, the surface area kept getting smaller as the dimensions got closer in size.
Teacher: Great observation! Rectangular prisms with the same volume that are more cube-like tend to have less surface area than prisms that are less cube-like. This information is very useful in the "real world," especially to packing engineers who design boxes to ship all those things that people buy online. Does anyone have ideas about why this is useful information?
Student: No clue.
Teacher: Think about what surface area is and why it is important to someone who designs boxes?
Student: Surface area tells you how much cardboard is needed to make the box.
Teacher: Yes, and why would that be important?
Student: Boxes that take less cardboard will cost less to make.
Teacher: And less expense means more profit for businesses.
Sample student work:
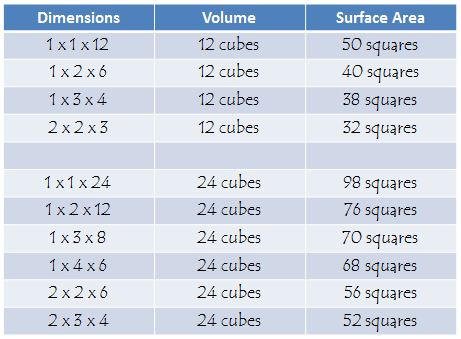
Sidebar: Note that counting the number of prisms with a certain volume and whole number side length is the same as counting the number of factorizations of that volume into three factors, not taking account of the order of the factors.
Resources
Teacher Notes
- Students come with many experiences determining area and perimeter of two-dimensional shapes, but have limited experiences with three-dimensional objects. It is important that students have multiple opportunities to determine surface area and volume of three-dimensional objects in order to develop understanding of the concepts. Measuring area by covering shapes with squares and measuring volume by filling objects with cubes can be worthwhile for many students. These activities reinforce the concept that area uses same-size square units to cover a shape and volume uses same-size cubic units to fill a space without gaps or overlaps, and will help students to choose appropriate units.
- Teachers can help students develop formulas for the surface areas and volumes of prisms by having them construct models, measure the dimensions, estimate the areas and volumes, and look for patterns and relationships related to lengths, areas, and volumes, In their work with three-dimensional shapes, they can make use of what they know about two-dimensional shapes. For example, students can determine the surface areas of three-dimensional rectangular prisms by relating them to two-dimensional nets consisting of three pairs of congruent rectangles;
- Experiences with nets will benefit students who have difficulty visualizing the unseen faces in a two-dimensional drawing of a three-dimensional object;
- Working with open containers first will help students who struggle to visualize volume for closed containers;
- Students will benefit from including irregular shapes in measurement experiences. This will help them develop the understanding that area is always measured in square units and volume is always measured in cubic units;
- The misconception that surface area can be found when the volume is known comes from the incorrect over-generalization of the very special relationship that exists for a cube. This can be addressed by having students use a fixed number of stacking cubes to build different rectangular prisms and then recording the corresponding surface area of each arrangement. Because the number of cubes is the same, the volume is identical for all, but the surface area varies. Although one counterexample is sufficient to demonstrate mathematically that volume does not determine surface area, many examples may be necessary to dispel the misconception. Some students will benefit from repeating this activity with several different fixed volumes.
Students create many configurations with the same volume, but differing surface areas.
Students use an interactive applet to investigate the formula for the volume of a rectangular prism. Students will analyze how changing the dimensions of a prism affects its volume.
Students can explore how to decompose shapes and make other shapes. Pieces can slide, flip, and turn.
Additional Instructional Resources
- Exploring Surface Area, Volume, and Nets (Object Interactive)
This interactive website allows students to explore the concepts of surface area,
volume, 3D shapes, and nets. It includes print activities, solutions, and learning
strategies. - Shape ExplorerThis website allows students to practice calculating area and perimeter for irregular shapes on a grid.
This article that describes a unit on measurement that uses the legend of Paul Bunyan to model and connect the concepts of length, area, and volume to scalefactor and proportion.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks:
- What strategies can be used to assist students connect three-dimensional objects to two-dimensional drawings?
- What strategies can be used to assist students in identifying hidden faces of three-dimensional objects in two-dimensional drawings?
- What strategies can be used to help students develop formulas for surface area and volume, rather than relying on rote memorization?
- Why it is important for students to find the surface area and volume of three-dimensional objects simultaneously?
- How can you assist students to understand decomposition (shapes can be taken apart) and composition (shapes can be put together)?
- Why is it important for students to estimate perimeter and area of irregular figures?
Materials
Measurement in the Middle Grades: Insights from NAEP and TIMSS
- NCTM: A Research Companion to Principles and Standards for School Mathematics (Details can be found in the References section.)
Chapter 12, Research on Students' Understanding of Area Measure (pp. 184-186) and Volume Measure (pp. 186-187).
Keeley, P., & Rose, C. (2006). Mathematics curriculum topic study. Thousand Oaks, CA: Corwin Press.
Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
Developing essential understanding of ratios, proportions & proportional reasoning grades 6-8. (2010). Reston: VA: National Council of Teachers of Mathematics, Inc.
Curriculum focal points for prekindergarten through grade 8 mathematics. (2006). Reston: VA: National Council of Teachers of Mathematics, Inc.
Assessment
(DOK Level 1)
- Find the area of the trapezoid shown below.
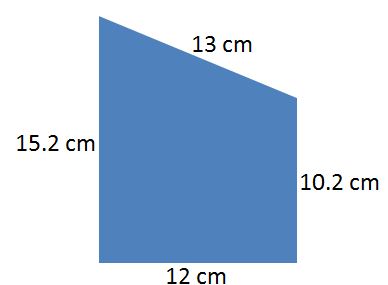
Answer: 152.4 cm2
(DOK Level 1)
2. Find the volume of the rectangular prism shown below.
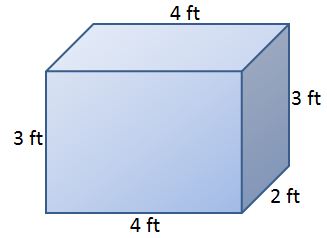
a) 16 ft3 b) 24 ft3 c) 144 ft3 d) 288 ft3
Answer: b
(DOK Level 2)
3. How much material is needed to make the kite shown below?
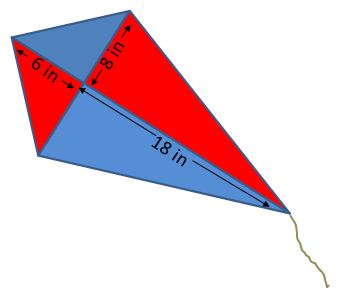
Answer: 96 in2 of red and 96 in2 of blue, or a total of 192 in2
(DOK Level 2)
4. Use the drawing below to answer the following questions.

Which of the following is the best estimate of the perimeter of the "x" shown?
a. 30 units b. 45 units c. 60 units d. 75 units
Answer: c
b. Which of the following is the best estimate of the area of "x" shown?
a. 90 square units
b. 115 square units
c. 140 square units
d. 165 square units
Answer: b
(DOK Level 4)
5. Find the volume and surface area of the triangular prism that can be formed from the net shown below. Justify your answers.
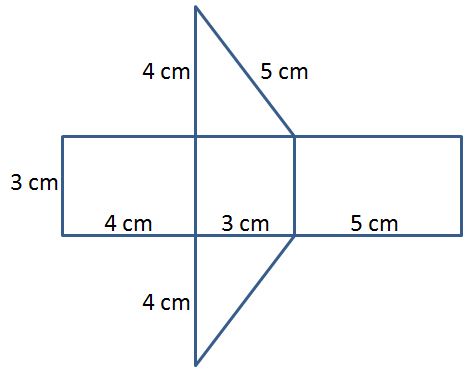
Answers:
The volume of the triangular prism is 18 cm3. Volume can be found by multiplying the area of the base times the height. Since this is a triangular prism, the triangles are considered the bases whose area can be found using the formula A = $\frac{b\times h}{2}$. The height of the triangular prism is 3. Using the formula V = Bh, V = $\frac{3 cm\times 4 cm}{2}$ x 3 cm = 6 cm2 x 3 cm = 18 cm3.
The surface area of the triangular prism is 48 cm2. Surface area can be found by adding the areas of individual faces. A triangular prism has five faces, two congruent triangles and 3 rectangles.
Area of rectangle shown on left: 3 cm x 4 cm = 12 cm2 ;
Area of rectangle shown in center: 3 cm x 3 cm = 9 cm2;
Area of triangle shown on top: $\frac{3 cm\times 4 cm}{2}$ = 6 cm2;
Area of triangle shown on bottom: $\frac{3 cm\times 4 cm}{2}$ = 6 cm2;
Area of rectangle shown on right: 5 cm x 3 cm = 15 cm2;
Surface Area = 12 cm2 + 9 cm2 + 6 cm2 + 6 cm2 + 15 cm2 = 48 cm2.
Differentiation
Struggling Students
- Give students 16, 20, or 24 color tiles. Ask them to use the tiles to make rectangles, then record the perimeter and area for each rectangle. Student should discover that although the area remains the same for a set number of color tiles, the perimeter can vary. Have students create irregular polygons, as well.
- Go on a shape walk. Ask students to identify two-dimensional shapes and three-dimensional objects in the real world.
- Two and Three Dimensional Shapes This website allows students to see all sides of a three dimensional object. It also identifies attributes of two dimensional shapes.
- Provide nets for students to fold as they learn about various prisms.
- Provide objects that students can cover with squares to determine surface area and fill with cubes to determine volume.
- Post and label pictures of squares, rectangles, rhombuses, parallelograms, trapezoids, and kites.
- Post and label pictures of cubes, triangular prisms, and rectangular prisms. Discuss with students that prisms are named by the shape of their base.
- Place various three-dimensional prisms inside a bag. Have students randomly select one to name, describe, and identify attributes.
- Play "20 questions" with students. One person selects a geometric figure or shape and the other persons ask yes-no questions until they determine what it is
- Use graphic organizers, such as the Frayer model shown below, for vocabulary development.
- Water Bottle Designs and Measures provides open-ended projects that will motivate your students to think at higher levels.
- Ratios of Linear, Area, and Volume Measures in Similar Solids, an article that provides information on using paper balloon origami to discover the relationship between corresponding distance, area, and volume measures in similar solids.
- The Legend of Paul Bunyan, provides a unit on measurement that uses the legend of Paul Bunyan to model and connect the concepts of length, area, and volume to scale factor and proportion.
- Have students explore what happens to surface area and volume of a rectangular prism when all the dimensions are doubled, tripled, or quadrupled.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) | Teachers are: (descriptive list) |
using objects that can be covered with squares and filled with cubes to explore the concepts of surface area and volume | providing students with hands-on investigations for determining surface area and volume |
having frequent experiences that involve determining surface area and volume simultaneously | posing questions that require students to examine surface area and volume simultaneously to help them distinguish between the concepts |
using formulas to solve area and volume problems | posing questions that require students to solve simple equations using area and volume formulas |
solving meaningful real-world area and volume problems | using the real-world as a source of relevant area and volume problems |
looking for patterns in data when scale factors are applied to linear dimensions | drawing students' attention to patterns that result when scale factors are applied to linear dimensions |
representing three-dimensional objects with two-dimensional drawings, including nets | helping students identify dimensions and make connections between two-dimensional drawings and three-dimensional objects |
developing formulas for area and volume through investigation | asking students to generalize procedures for finding area and volume and justify their findings |
using ratios to deepen their understanding of relationships in geometric figures | drawing attention to the fact if a/b is the ratio of the corresponding linear dimensions of two rectangles, then the ratio of their areas will be (a/b)2 and the ratio of their volumes will be (a/b)3 |
using coordinate grids to find perimeter and area of irregular figures | asking students to estimate perimeter and area of shapes that cannot be decomposed into common figures |
discussing and writing about the strategies used to determine area and volume | requiring students to communicate their thinking, both verbally and in written form |
justifying area and volume formulas | asking students to use mathematical properties to explain their thinking and justify results |
choosing and labeling units appropriately | emphasizing the different between units, square units, and cubic units |
estimating answers before performing calculations | helping students to develop a sense of reasonableness |
describing how changes in the dimensions of figures affect perimeter, area, and volume | providing opportunities for students to communicate their thinking to peers, teachers, and others |
Parent Resources
- Geometric Formula Review, a website with formulas commonly used for surface area and volume;
- Burns, M., & Tilley, D. (1997). Spaghetti and meatballs for all!: A mathematical story. New York: Scholastic. (Seating for a family reunion gets complicated as more and more relatives arrive. Works with both area and perimeter.)
