6.2.3 Represent & Solve Equations
Represent real-world or mathematical situations using equations and inequalities involving variables and positive rational numbers.
For example: The number of miles m in a k kilometer race is represented by the equation m = 0.62 k.
Solve equations involving positive rational numbers using number sense, properties of arithmetic and the idea of maintaining equality on both sides of the equation. Interpret a solution in the original context and assess the reasonableness of results.
For example: A cellular phone company charges $0.12 per minute. If the bill was $11.40 in April, how many minutes were used?
Overview
Standard 6.2.3 Essential Understandings
Students at this level begin to develop the ability to generalize numerical relationships and express mathematical ideas concisely using expressions and equations (e.g., three more as x + 3, doubling as 2n, commutativity as a + b = b + a). Activities, problems, and discussions are used to build the belief that algebraic expressions behave in the same way as numerical expressions. Before students can use algebraic representations to generalize mathematical relationships, it is essential for them to first explore the numerical representations with which they are familiar to gain a sense of the relationship between the numerical and the algebraic. By connecting representations of numerical relationships that students have acquired prior to grade 6 to more formal algebraic representations, students build a strong understanding of how the algebraic representation is related to what they know, the numerical relationship. Once students understand properties applied to numerical expressions and equations, they will be able to use algebraic symbols flexibly to represent mathematical relationships and to solve problems. Number sense, properties of operations, and the idea of maintaining equality on both sides of an equation are used to solve simple algebraic equations and inequalities whose solutions are positive rational numbers. Students develop the skills to use expressions, equations, formulas, and inequalities to solve problems and interpret solutions in the original context.
All Standard Benchmarks
6.2.3.1 Represent real-world or mathematical situations using equations and inequalities involving variables and positive rational numbers.
6.2.3.2 Solve equations involving positive rational numbers using number sense, properties of arithmetic and the idea of maintaining equality on both sides of the equation. Interpret a solution in the original context and assess the reasonableness of results.
Benchmark Group A
6.2.3.1 Represent real-world or mathematical situations using equations and inequalities involving variables and positive rational numbers.
6.2.3.2 Solve equations involving positive rational numbers using number sense, properties of arithmetic and the idea of maintaining equality on both sides of the equation. Interpret a solution in the original context and assess the reasonableness of results.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Understand that a variable represents any value that makes a statement true, and may represent one value, many values, or no value;
- Generalize additive and multiplicative numerical relationships and express them using algebraic representations (e.g., x + 2, 2x);
- Use the idea of maintaining equality on both sides to solve equations and inequalities that involve positive rational numbers;
- Understand and apply inverse operations (addition-subtraction and multiplication-division) when solving equations and inequalities;
- Represent and solve real-world and mathematical situations using equations and inequalities;
- Interpret solutions to real-world problems represented by equations and inequalities in its original context.
Work from previous grades that supports this new learning includes:
- Determine whether an equation or inequality involving a variable is true or false for a given value of the variable;
- Represent real-world situations using equations and inequalities involving variables. Create real-world situations that correspond to equations and inequalities;
- Evaluate expressions and solve equations involving variables when values for the variables are given;
- Solve real-world and mathematical problems requiring addition, subtraction, multiplication and division of multi-digit whole numbers. Use various strategies, including the use of technology, inverse relationships between operations, and the context of the problem to assess the reasonableness of results.
NCTM Standards:
Represent and analyze mathematical situations and structures using algebraic symbols
- Develop an initial conceptual understanding of different uses of variables;
- Use symbolic algebra to represent situations and to solve problems, especially those that involve linear relationships;
- Recognize and generate equivalent forms for simple algebraic expressions and solve linear equations.
Common Core State Standards (CCSS):
6EE (Expressions and Equations) Apply and extend previous understandings of arithmetic to algebraic expressions.
6EE.7 Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all nonnegative rational numbers.
6EE.8 Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
Misconceptions
Student Misconceptions and Common Errors
- Students think that variables can represent only one number;
- Students ignore letters used to represent unknowns when simplifying; for example, 3m + 2 = 5, or 3m + 2 = 5m;
- Students do not distinguish between letters used to represent variables and letters used to represent units of measure (e.g., 5m and 5 m as in meters, or 3h and 3 h, as in hours);
- Students think of the equal sign as a symbol that means "to calculate" rather than "is the same as;"
- Students struggle to solve equations such as 5 = x + 2 or 10 = 2x, where the variable is on the right side;
- Students may attempt to solve equations such as 5x + 2 = 15 by dividing by 5 before subtracting 2, thus "undoing" the multiplication before the addition;
- Students may believe that equations always result in whole number solutions.
Vignette
In the Classroom
The following vignette shows how a teacher helps students learn to generalize numerical relationships and express mathematical ideas concisely using expressions and equations.
Teacher: Here is a representation of houses that we call the 1st, 2nd, 3rd, and 4th house. Let's assume that the pattern of adding one more column to the previous house continues. If the pattern continues, how many total blocks are in the 5th house?
Student: I noticed that every house had 2 squares with a triangle on top added to the house before it. So I drew the 5th house. Then I counted the shapes. There were 15 shapes in the 5th house.

Teacher: So you used a counting strategy. First you built the model and then counted the total number of shapes. What other strategies could be used?
Student: I realized that I didn't have to actually draw the houses. I could just write down the number of shapes in each house. There were 3 shapes in the 1st house, 6 in the 2nd, 9 in the 3rd, and so on. So I made a table that shows how the number of the house, 1,2,3,4, goes with the number of shapes for that house, 3, 6, 9, 12.
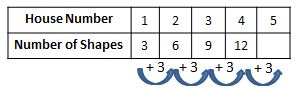
Teacher: Interesting. You found a pattern in the number of shapes in each house, and then organized the pattern using a table. Since each house had three more shapes than the house before it, you used 12 + 3 to find the answer. 12 + 3 is called a numerical expression. It is a numerical expression because it contains numbers and an operation symbol. There are no unknowns in a numerical expression; all the values are specified. Since the value of 12 + 3 is 15, we can write 12 + 3 = 15. This is called a numerical equation because it is a mathematical sentence formed by placing an equal sign between the expression 12 + 3 and the number 15. The equal sign indicates that the value of one side of the equation is the same as the value on the other side. Because we know that 12 + 3 has the same value as 15, we know that this equation is true. As with numerical expressions, there are no unknowns in a numerical equation. All the values are specified.
Teacher: How can these two strategies be used to find the number of shapes in the 8th house?
Student: I know how to find the answer by using the counting method. When I draw the 6th, 7th, and 8th houses and count the number of shapes in the 8th house, I get 24 shapes.

Student: The other strategy also works. Since I already know that there are 15 shapes in the 5th house and that the rule for the pattern is add 3, I can just extend the pattern to find the number of shapes in the 8th house.
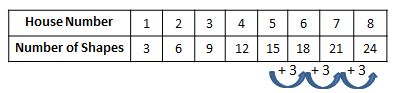
Teacher: I see. Let's think about using these two strategies to find the number of shapes in the 100th house of 500th house.
Student: Are you serious? That's going to take a long time.
Teacher: Why do you say that?
Student: Because to find the number of shapes in the 500th house using the counting method, I'd have to draw all the houses before I could count. That's going to take forever.
Student: I agree. Extending the pattern by using the rule to add 3 might be faster, but it will still take a long time. You'd have to find the number of shapes in every house up to the 500th house.
Teacher: Good point. Perhaps we can find a faster way to find the number of shapes in the 500th house. Let's explore the relationship between the house number and the number of shapes needed to build it. Sometimes it's easier to see those relationships when the table is created in a vertical format. You're probably familiar with this format from your experiences with graphing ordered pairs on a coordinate grid.
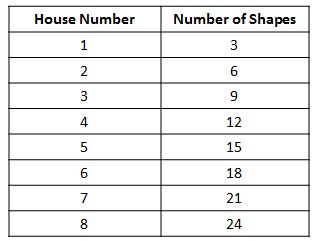
Teacher: As you look at this table, what is the relationship between each house number and the number of shapes in that house?
Student: I see it now. The number of shapes in a house is 3 times the house number. The first house has 1 x 3 = 3, or 3 shapes; the second house has 2 x 3 = 6, or 6 shapes, the 8th house has 8 x 3 = 24, or 24 shapes, and so on. I think I see how to use this relationship to find the 500th house!
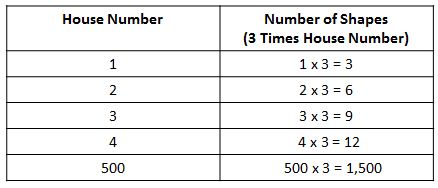
Teacher: Can you explain it to us?
Student: Sure. I can multiply 500 by 3 to get the number of shapes in the 500th house: 500 x 3 = 1500 shapes in the 500th house.

Teacher: You're using algebraic thinking when you say, "The number of shapes in a house is 3 times the house number." Since we know that we can multiply the house number by 3 to find the number of shapes in any house, we can use algebra to write this relationship concisely. This is the one purpose of algebraic representations, to write generalized mathematical relationships concisely or efficiently. To write the relationship between the house number and the number of shapes in the house, we need to replace the numbers that can change with some other symbol. We can choose any symbols to represent the numbers, but we usually use letters. Let's start by using a sentence to describe the relationship between the house number and the number of shapes. What sentence describes that relationship?
Student: The house number times 3 is equal to the number of shapes.
Teacher: Yes. Let's think about that statement. "The house number times 3 is equal to the number of shapes." If we let the letter h represent the house number and the letter s represent the number of shapes, we can write s = 3 x h, or s = 3h.
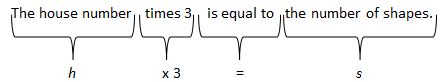
This equation is a very concise mathematical sentence that says the same thing. And we can use this equation to determine the number of shapes that would correspond to any house. For example, if the house number is 110, then the corresponding number of shapes is s = 3 x 110 = 330. Let's add another row to our table to express this relationship.
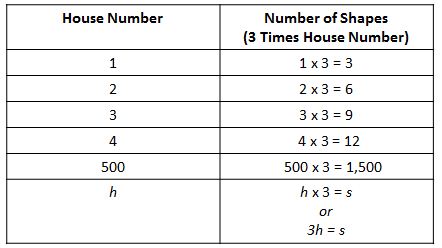
Teacher: Now that we have a powerful representation of the relationship between the house number and the number of shapes, we can use it to find the number of shapes in any house number. How can we use the equation to find the number of shapes in the 800th house?
Student: I know. The house number is 800, so h is 800. I can substitute 800 in for h in the equation, so 800 x 3 = s. I multiply 800 by 3 and get 2,400. If the house number is 900, h= 900, and 900 x 3 = 2,700. Wow! I can do this for any number, even 1,234,567,890. This is a lot faster than drawing houses.
Teacher: That's right. Algebraic representations help us write mathematical relationships in efficient ways so that we can use them to solve problems.
Sidebar: It is important that students understand that this relationship can be written in several ways; e.g., 3 x h = s, h x 3 = s, 3h = s, and s = 3h.
Teacher: We know that the equation s = 3h can be used to find s, the number of shapes in a house given h, the house number. I'm wondering if we could use that same equation to find h, the house number, if we were given s, the number of shapes. For example, if I told you that the number of shapes was 39, could you tell me the house number?
Student: I can. I think its house number 13.
Teacher: What makes you think that there are 39 shapes in house number 13?
Student: Well, I know the number of shapes s = 3h, so I substituted 39 for s in the equation.
s = 3h
39 = 3h
Then I need to find a number that when multiplied by 3 gives 39. I know that 3 x 13 is 39, so h must be 13.
Teacher: That makes sense. What would you have done if I told you that the number of shapes was 456?
Student: Oh, that's a harder one. I don't know what number times 3 will give me 456.
Student: That is a harder problem, but I think I know how to figure it out.
Teacher: How would you do that?
Student: By dividing. Multiplication and division undo each other. Since I want to know what number times 3 is 456, I can divide 456 by 3 to find the answer. 456 ÷ 3 = 152, so I think house number 152 has 456 shapes.
Teacher: Yes, multiplication and division are inverse operations and "undo" each other. For example, since 15 = 3 x 5, we know that 15 ÷ 3 = 5 and 15 ÷ 5 = 3. You used that same idea to find the house number for 456 shapes. We know that the number of shapes, 456, can be found by multiplying 3 times the house number. Since 456 = 3 x h, we can "undo" that multiplication and find h by dividing 456 by 3. 456 ÷ 3 = 152, so house number 152 has 456 shapes.
Teacher: Today we found a rule that can be used to easily find the number of shapes given the house number: s = 3h. Your assignment for tomorrow is to write a rule that can be used to easily find the house number given the number of shapes. Use h to represent the house number and s to represent the number of shapes. You may want to start with a sentence that expresses your rule before writing it with symbols. Your rule will be a powerful representation that can be used to efficiently solve problems for any given number of shapes. Good luck!
Resources
Teacher Notes
● Students may have developed the misconception that variables represent only one number from solving equations such as x + 3 = 5, where x = 5 is the only value that makes the statement true. Using equations such as P = 7.00h, where P represents pay in dollars and h represents number of hours worked at $7.00 per hour, to determine pay for various numbers of hours will help students recognize that variables represent quantities that can change. As students begin to explore algebraic representation, they need to understand that a variable represents any value that makes the statement true. A variable, then, may represent one value, many values, or no value (empty set).
● The misconception that variables can represent only one number can be addressed using an example such as x ≥ 5. Graphing the solution on the number line will help students see that there are many (infinite) solutions. Using a real-life context for the inequality will also help students understand that there are multiple solutions. For example, a student who asks to borrow at least $5 will have their needs met if they receive $5, $50, $500, etc.
● The extensive use of concrete materials and pictorial representations of algebraic expressions will help students understand that 3m + 2 is not equivalent to either 5 or 5m and will support students in identifying like terms that can be combined.
● Students that confuse letters used as variables with letters used to abbreviate units of measure will benefit from writing out entire words for units of measurement rather than using abbreviations. It is also helpful to avoid using letters for variables that are used to abbreviate units of measurement, such as m and h, until students have developed a better understanding of how letters are used as variables.
● An important aspect of studying equations is applying the appropriate meaning for the equals sign. The equal sign in an equation sets up a condition in which the expression on the left of the equals sign has the same value as the expression on the right. This condition determines which numbers solve the equation. One way to assess whether students truly understand the meaning of the equal sign as a symbol that means "is the same as" or whether they think of it as a symbol that means "to calculate" is to have them fill in the blank in an equation such as 6 + 8 = ____ + 5. Students who answer "14" need attention to develop the appropriate meaning for the equal sign.
● Students can use the idea of a balance to help develop their understanding of an equation as a set of conditions. Representing equations with the balance model builds on students' understanding that if the sides of the balance are level, they have the same "weight." Students can translate this analogy to modeling equations. If they represent one expression on one side of the balance and another expression on the other side of the balance and the sides are the same height, the first expression has the same value as the other expression and the equation is true. If the two sides of the balance are level, then the fulcrum of the balance becomes a representation of the equal sign.
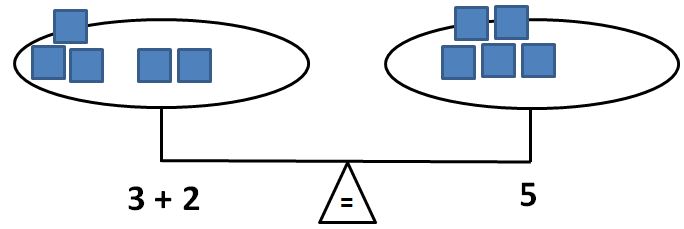
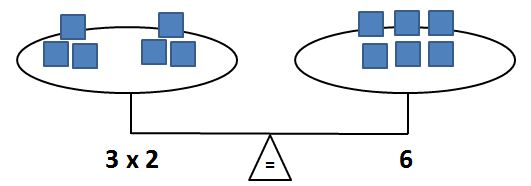
● Students who struggle to solve equations with variables on the right side will benefit from using the reflexive property to rewrite those equations. It will be helpful to connect to students' previous experiences of the reflexive property with numbers (e.g. 5 = 3 + 2 is the same as 3 + 2 = 5, therefore 5 = x + 2 is the same as x + 2 = 5; 10 = 2 x 5 is the same as 2 x 5 = 10, therefore 10 = 2x is the same as 2x = 10).
● As students begin to learn how to find the values for variables that solve equations, they need to develop an understanding of the properties of equality for addition, subtraction, multiplication, and division. For example, the additional property of equality states that if you add a number to both sides of a true equation, the equation stays true. Teachers should present these properties first using numerical equations. Students' understanding of how the properties are applied in numerical equations will lead to the belief that the properties work in the same way in algebraic equations. Examples such as those shown below will be helpful in accomplishing this goal.
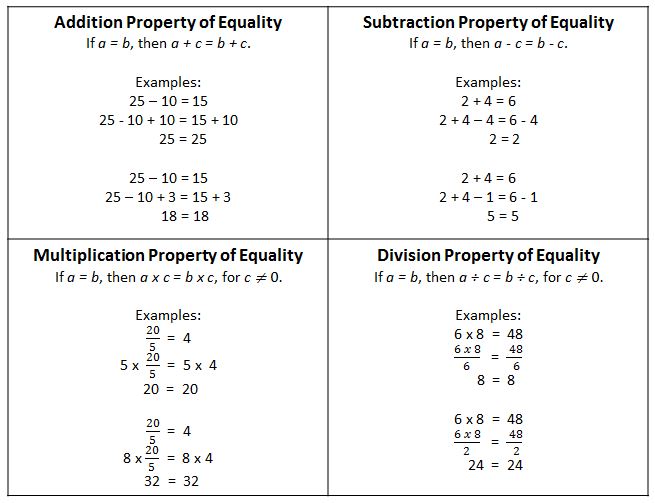
● Give students opportunities to apply the properties of equality to numerical expressions until students begin to understand that the properties of equality are true for any number in any equation, other than dividing by 0, since that results in an undefined value.

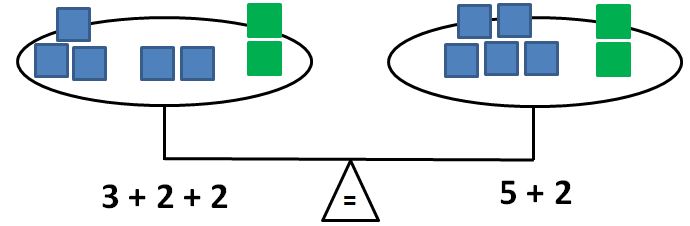
● Once students have gained an understanding of the equality properties in numerical equations, they can move to applying the properties to algebraic equations. A balance model can be used to demonstrate the multiplication property of equality when an unknown is involved.
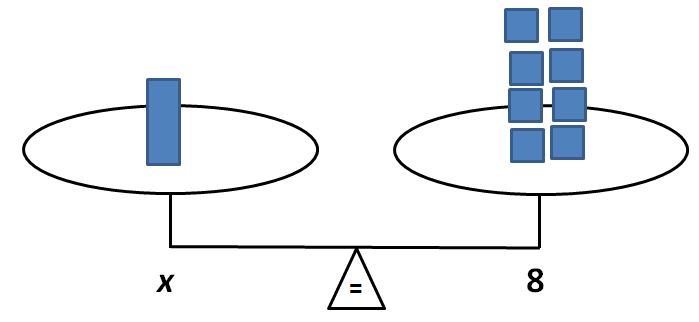
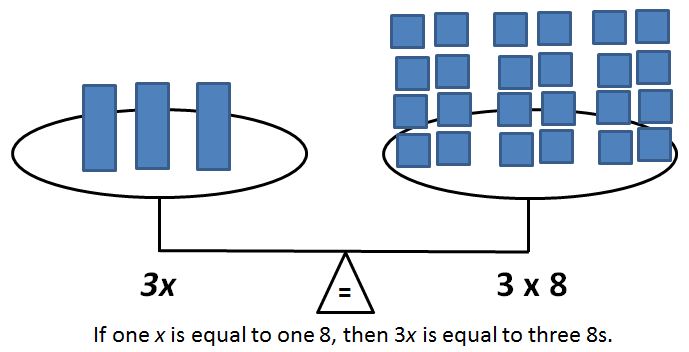
● When students have built the understanding of the properties of equality, they are ready to learn how to use these properties to solve equations. It is essential that students gain this understanding first so that they can apply the properties of equality to algebraic equations in a meaningful way.
● Teachers can use examples like the ones shown below along with concrete representations, such as algebra tiles and balances, to teach students how to use inverse operations and the respective equality property to solve different types of equations. In each example, it is important to discuss how the choice of the operation and number used was made to find the value of the variable.
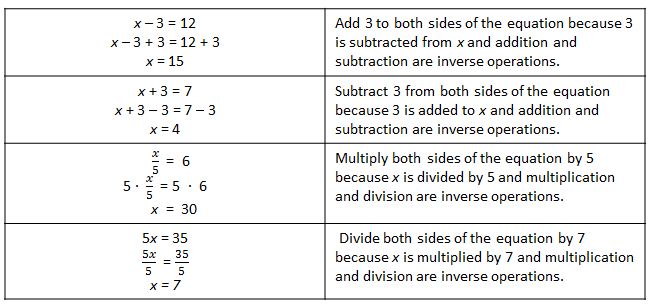
● Remind students that when solving equations, they are actually working backwards to reverse the order of operations and "undo" them. Since addition and subtraction are the last operations to be performed, they are the first operations that need to be "undone." Addition and subtraction must always be "undone" before multiplication and division. Using a balance or pictorial representation to solve equations will also help students see the necessity of working backwards through the order of operations when solving equations and inequalities;
● It is important that students are presented with equations whose solutions involve positive fractions and decimals once they have gained an understanding of the process. This will help them understand that the properties of equality apply not only to whole numbers, but also to rational numbers.
EverythingBalancesOutintheEnd
In this 3-lesson sequence, students use a pan balance to study equality, order of operations, numerical and variable expressions, and other key algebraic concepts.
GeologyRocksEquations
In this lesson, students explore linear equations with manipulatives and discover various steps used in solving equations.
Additional Instructional Resources
Algebra Balance Scales
This virtual manipulative allows you to solve simple linear equations through the use of a balance beam. Unit blocks (representing 1s) and X-boxes (for the unknown, X), are placed on the pans of a balance beam.
evaluate: to find the value. To evaluate algebraic expressions, particular numbers are substituted for variables before calculating. Example: To evaluate 7x for x = 5, x is replaced with 5, resulting in 35.
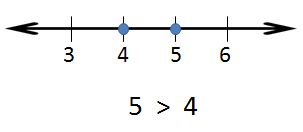
is greater than (>): a number "is greater than" another number if its value is larger than the compared number. Example:
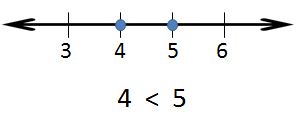
is less than (<): a number "is less than" another number if its value is smaller than the compared number. Example:
order of operations: the rules describing what sequence to use in evaluating expressions. All calculations are done left to right. The order is:
1. Parentheses and other grouping symbols; work from the innermost set using rules 2-4;
2. Exponents
3. Multiply or divide in the order the operations occur.
4. Add or subtract in the order the operations occur.
Example: 52 + (3 x 4 - 2) ÷ 5 = 52 + (12 - 2) ÷ 5
= 52 + 10 ÷ 5
= 25 + 10 ÷ 5
= 25 + 2
= 27
rational number: any number that can be expressed in the form ab, where a and b are integers and b ≠ 0. A rational number can always be represented by either a terminating or a repeating decimal. Examples: $\frac{2}{3}$; 4 (which can be expressed as $\frac{4}{1}$); 2.25 (which can be expressed as $\frac{225}{100}$.)
simplify (an expression): to rewrite by removing parentheses and by combining like terms. Examples: In 3x + 4 + 2 + 2x can be simplified as 5x + 6 and 3(2y + 4) - y can be simplified as 5y + 12
simplify (a fraction): to express in simplest form, or lowest terms. The numerator and denominator of proper fractions in simplest form have no common factor other than 1. Improper fractions and mixed numbers are in simplest form when the fraction part is proper and in simplest form. Examples: The numerator and denominator of $\frac{4}{8}$ share the common factor 4 so must be rewritten as $\frac{1}{2}$ to be in simplest form; $\frac{19}{3}$ written in simplest form is $6\frac{1}{3}$.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
How can student understanding of the equal sign be assessed?
- How can student understanding and experiences with numerical expressions and equations be used to connect to algebraic expressions and equations?
- What progression of problem-solving experiences might best help students to write, interpret, and use equations and expressions?
- What strategies can be used to help students understand how to solve equations using properties of operations and equality?
Materials
Details about these materials can be found in the References section.
● Algebraic Equations This article is from Benchmarks for Science Literacy, Chapter 9B, pp. 351-352.
● NCTM A Research Companion to Principles and Standards for School Mathematics
Chapter 9, Algebra: Research on Algebra Learning and Directions of Curricular Change, pp. 122-133.
Chapter 10, Algebra, pp. 138-141, Functions, pp. 141-142, Stasis and Change, pp. 142-148, Discussion, p. 148-149.
Keeley, P., & Rose, C. (2006). Mathematics curriculum topic study. Thousand Oaks, CA: Corwin Press.
Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
National Council of Teachers of Mathematics. (2010). Focus in grade 6 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics, Inc.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
Assessment
(DOK Level 1)
- Even during sleep, the average human heart pumps around 80 gallons of blood per hour. Solve the equation g ÷ 80 = 24 to find how many gallons g the heart pumps in 24 hours.
Answer: g = 1,920 gallons
(DOK Level 1)
2. Kai saved $225. He spent m dollars on a skateboard and had $28 left.
Write an equation to describe this situation.
Answer: 225 - m = 28
(DOK Level 2)
3. A train makes a 200 mile trip in 4 hours, traveling at a rate of r miles per hour.
Which equation describes this situation?
a. 200r = 4 b. 4 + r = 200 c. r - 4 = 200 d. 4r = 200
Answer: d
(DOK Level 4)
4. The perimeter P of the rectangle shown below is 24. Write and solve an equation to find its dimensions.
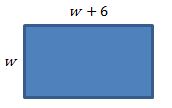
Answer: 2w + 2(w + 6) = 2w + 2w + 12 = 4w + 12 = 24; 4w = 12; w = 3; w + 6 = 3 + 6 = 9. The dimensions are 3 and 9.
Differentiation
It is essential that students understand the appropriate meaning of the equal sign as "the same as" rather than "to calculate." One way to assess this is to ask them to fill in the blank for a problem such as 6 + 8 = _____ + 5. Students who answer "14" need attention to develop the appropriate meaning for the equal sign.
Pan Balance - Numbers
This tool can be used to strengthen understanding and computation of numerical expressions and equality.
Spy Guys: Balancing Equations
This interactive lesson shows beginning concepts of pan balances.
- Have students generalize mathematical relationships in words before using symbols.
- Provide multiplication charts and/or calculators for students who struggle with basic facts.
- Provide graphic organizers with pan balances for students to make pictorial representations of equations.
- Use concrete materials and pictorial representations when solving equations and inequalities.
- Write verbal models for relationships before using symbols to express them.
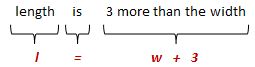
- Use pictorial representations to model relationships before using symbols to express them.
- Pair English Language Learners with students who have strong English language skills.
- Use graphic organizers such as the Frayer model shown below, for vocabulary development.
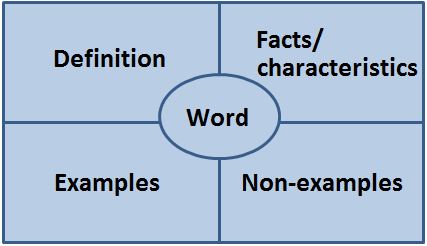
- Extending to Symbols
In this lesson, students explore the equivalence of two symbolic expressions. - Algebra Balance Scales
This virtual manipulative allows you to solve simple linear equations through the use of a balance beam. Unit blocks (representing 1s) and X-boxes (for the unknown, X), are placed on the pans of a balance beam. - Spy Guys: Balancing Equations
This interactive lesson shows beginning concepts of pan balances. - Equations (Food)
This interactive game asks students to match words, pictorial representations, and equations.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) | Teachers are: (descriptive list) |
understanding that the equal sign means "is the same as." | assessing students' understanding of the equal sign to identify students with the misconception that it means "to calculate." |
discovering that properties apply to algebraic expressions and equations in the same way as they did to numerical expressions and equations. | connecting students' previous experiences with numbers to algebra representations to build the belief that algebraic expressions and equations behave in the same way as numeric expressions and equations. |
using words and symbols to generalize numerical relationships. | asking students to use the language of algebra to express mathematical relationships concisely. |
using pan balances to explore properties of equality with numerical and algebraic expressions. | providing experiences with concrete and semi-concrete representations before moving to abstract. |
discussing, writing, and solving their own algebraic representations. | asking students to communicate their reasoning to others. |
solving equations by using number sense, properties of operations, and the idea of maintaining equality on both sides. | modeling a variety of strategies to solve equations. |
justifying solutions to equations. | asking students to explain why their answers are solutions. |
recognizing the use of algebra as a powerful problem-solving tool. | constructing problem-solving experiences with a purposeful progression that focus on how to write, interpret, and use equations and expressions. |
Parent Resources
Spy Guys: Balancing Equations
This interactive lesson shows beginning concepts of pan balances.
Solving Equations Lessons
This website provides instruction and practice in solving equations.
Equations and Inequalities - Addition and Subtraction
This website provides instruction and practice in solving addition and subtraction equations.
Solving One-Step Equations (Addition and Subtraction)
This video explains how to solve one-step equations involving addition and subtraction.
Solving One-Step Equations (Multiplication and Division)
This video explains how to solve one-step equations involving multiplication and division.
One Step Inequalities (Addition and Subtraction)
This video explains how to solve one-step inequalities involving addition and subtraction.
