6.1.3B Percent
Calculate the percent of a number and determine what percent one number is of another number to solve problems in various contexts.
For example: If John has $45 and spends $15, what percent of his money did he keep?
Overview
Standard 6.1.3 Essential Understandings
Students at this level model multiplication and division of fractions and connect these models to procedures for multiplying and dividing fractions. Place-value patterns are used to multiply and divide finite decimals by powers of 10. The relationship between decimals and fractions, as well as the relationship between finite decimals (i.e., a finite decimal multiplied by an appropriate power of 10 is a whole number), is used to understand and explain the procedures for multiplying and dividing decimals. Common procedures are used to multiply and divide fractions and decimals efficiently and accurately. Problem solving with positive rational numbers is extended to include arithmetic with decimals, fractions, and mixed numbers. Students build on understanding that percents are ratios per 100 to solve problems in various contexts that require finding percent of a number or what percent one number is of another.
All Standard Benchmarks
6.1.3.1 Multiply and divide decimals and fractions using efficient and generalizable procedures, including standard algorithms.
6.1.3.2 Use the meanings of fractions, multiplication, division and the inverse relationship between multiplication and division to make sense of procedures for multiplying and dividing fractions.
6.1.3.3 Calculate the percent of a number and determine what percent one number is of another number to solve problems in various contexts.
6.1.3.4 Solve real-world and mathematical problems requiring arithmetic with decimals, fractions and mixed numbers.
6.1.3.5 Estimate solutions to problems with whole numbers, fractions and decimals and use the estimates to assess the reasonableness of results in the context of the problem.
Benchmark Group B
6.1.3.3 Calculate the percent of a number and determine what percent one number is of another number to solve problems in various contexts.
What students should know and be able to do [at a mastery level] related to these benchmarks
- Understand fractions, percents, and decimals as ways of representing rational numbers;
- Convert among fractions, percents, and decimals and decide which form to use in a given situation;
- Know fraction and decimal equivalents for common percents; e.g.,1%, 10%, 25%;
- Use fractions and decimals to calculate the percent of a number; e.g., 20% of 50 can be found with 0.2 x 50 or $\frac{1}{5}$ x 50;
- Use the concept of percent as parts out of 100 and find equivalencies to determine what percent one number is of another; e.g., What percent 12 is of 15 can be found with $\frac{12}{15}$ = 0.8 = 80%;
- Solve problems in various contexts that require determining the percent of a number;
- Solve problems in various contexts that require determining what percent one number is of another;
- Estimate answers to percent problems using common fraction and decimal benchmarks and use the results to assess reasonableness.
Work from previous grades that supports this new learning includes:
- Recognize and generate equivalent decimals, fractions, mixed numbers and improper fractions in various contexts;
- Multiply and divide decimals and fractions, using efficient and generalizable procedures, including standard algorithms;
- Round numbers to the nearest 0.1, 0.01 and 0.001;
- Understand that percent means parts out of 100 or ratios to 100;
- Determine equivalencies among fractions, decimals and percents; select among those representations to solve problems;
- Estimate products and quotients of multi-digit whole numbers by using rounding, benchmarks, and place value to assess the reasonableness of results;
- Estimate solutions to arithmetic problems in order to assess the reasonableness of results.
NCTM Standards:
Work flexibly with fractions, mixed numbers, and decimals to solve problems
- Build on prior knowledge from previous grade levels and everyday life;
- Use of decimals and fractions includes measurements and comparisons;
- Ensure solid understanding of context when deciding among differing representations for equivalency and moving flexibly between them;
Understand and use the associative, commutative, and distributive properties to simplify computations with integers, fractions, and decimals
- Use mathematical properties to simplify many computations involving fractions and decimals;
- Use common procedures to multiply and divide fractions and decimals efficiently and accurately;
Develop and analyze algorithms for computing with fractions, decimals, and integers and develop fluency in their use
- Develop own methods of computation and sharing results with class;
- Explain why methods chosen and subsequent solutions are reasonable;
- Compare and evaluate personal method with traditional algorithms;
Understand and use the inverse relationship of multiplication and division to simplify and solve problems
- Be mindful of the decision of when to multiply or divide when working with fractions, mixed numbers, or decimals;
- Increase understanding of division as being repeated subtraction rather than just a rote procedure of invert and multiply;
- Select appropriate methods and tools for computing with fractions and decimals from among mental computation, estimation, calculators or computers, and paper and pencil, depending on the situation, and apply the selected methods
Learn when an exact answer or an estimate is needed;
Identify which computational method should be chosen;
Evaluate reasonableness of solution;
Increase mental computation and estimation.
Common Core State Standards (CCSS):
5BTB (Number And Operations In Base Ten) Perform operations with multi-digit whole numbers and with decimals to hundredths.
5NTB.7 Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
5NF (Number And Operations--Fractions) Use equivalent fractions as a strategy to add and subtract fractions.
5NF.2 Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers.
5NF.4 Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
5NF.6 Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
5NF.7 Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions.
5NF.7.c Solve real world problems involving division of unit fractions by non-zero whole numbers and division of whole numbers by unit fractions, e.g., by using visual fraction models and equations to represent the problem.
6NS (Number System) Apply and extend previous understandings of multiplication and division to divide fractions by fractions.
6NS.1 Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem.
6NS.3 Fluently multiply and divide multi-digit decimals using the standard algorithm for each operation.
6RP (Ratios And Proportional Relationships) Understand ratio concepts and use ratio reasoning to solve problems.
6RP3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
6RP3.c Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.
7NS (Number System) Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers.
7NS.3 Solve real-world and mathematical problems involving the four operations with rational numbers.
Misconceptions
Student Misconceptions and Common Errors
- Students incorrectly translate among fractions, decimals, and percents (e.g., 5% is translated to $\frac{1}{5}$, 5, or 0.5; $\frac{1}{100}$ is translated to 0.01%; 2.4% is translated to 2.4).
- Students may not convert percents to fractions or decimals before multiplying (e.g., use 2.5 x 12 to find 2.5% of 12).
- Students struggle to estimate solutions to problems involving percents greater than 100% or less than 1%.
- Students believe that increasing a number by 10% and then decreasing the result by 10% will result in the original number.
Vignette
In the Classroom
The following vignette shows students using survey data to find percent of a number and what percent one number is of another.
Teacher: The student council surveyed 25 students to find out what kind of pizza they wanted at the sixth grade class party next week. Here are the results.
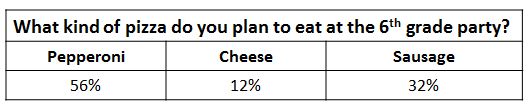
The table shows that 56% of the students plan to eat pepperoni pizza. How many students is that?
Student: 56.
Student: I don't agree. Only 25 students were surveyed, so it would be impossible that 56 students chose pepperoni.
Teacher: That's true. So how can we figure out how many students chose pepperoni?
Student: Well, percent means out of 100, so 56% means that 56 out of 100 students chose pepperoni. We're trying to find how many students out of 25 chose pepperoni. Since 25 is $\frac{1}{4}$ of 100, we can just divide 56 by 4 and get 14 students.
Teacher: How do you know that 14 students out of 25 is the same as 56 students out of 100?
Student: Easy. They're equivalent fractions: $\frac{56\div 4}{100\div 4}=\frac{14}{25}$.
Teacher: Nicely done. What other strategies could be used to find 56% of 25?
Student: I solved the problem in sort of the same way. First I wrote 56% as a fraction, $\frac{56}{100}$. Then I simplified it to$\frac{14}{25}$. That's 14 out of 25, so 14 students chose pepperoni.
Teacher: Yes, that's another strategy that can be used to solve this problem. But what would you have done if 32 students had taken the survey instead of 25? Would your strategy still work?
Student: No, because the denominator would need to be 32.
Teacher: Does anyone else have a strategy that might work?
Student: We could change the percent to a decimal and multiply, rather than using a fraction.
Teacher: Tell me more.
Student: 56% is the same as 56 hundredths or 0.56. To find 56% of 25, you multiply 0.56 x 25. You get the same answer, 14.
Student: Wait a minute. Could I do the same thing, but use the fraction for 56% instead of the decimal?
Teacher: Show me what you mean.
Student: Let me try it. Oh, it works!
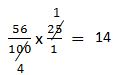
Teacher: Yes, it does; and 14 students seems like a reasonable answer since 56% is a little more than half and 14 students is a little more than half of 25. These percents are based on the survey results of 25 sixth graders, but there are actually a total of 92 students in the sixth grade. If 12% of the 92 students eat cheese pizza, how many students is that?
Student: It's 4 students.
Teacher: How did you find your answer?
Student: By subtracting. 92 is 8 less than 100, so I subtracted 8 from 12. That's gives me 4.
Teacher: I understand your thought process. Let's talk about percent for a moment. What does the word percent mean?
Student: Per hundred, or out of 100.
Teacher: Exactly! Percent is a ratio that has the amazing ability to stretch or shrink so that it always compares something to 100. We stretch or shrink things with scale factors. Scale factors are numbers we use to multiply, and cause a value to increase or decrease by a direct comparison to the original value. We use scale factors larger than 1 to stretch and scale factors between 0 and 1 to shrink. For example, multiplying by 2 will stretch something to twice its original size. Multiplying by $\frac{1}{2}$ will shrink something to half its original size. Now let's go back to the pizza problem. We're trying to find 12% of 92. 12% means 12 out of 100. Because there are a total of 92 students, the denominator needs to shrink from 100 to 92. Did you shrink the ratio by using a scale factor?
Student: No, I tried to shrink it with subtraction. I suppose that changed the ratio.
Teacher: Yes, adding or subtracting the same amount to the numerator and denominator of fractions does not result in equivalent fractions. That strategy doesn't work. Who tried another strategy to find 12% of 92?
Student: I found the scale factor.
Teacher: Show me what you did.
Student: First I wrote the fractions.
$\frac{12}{100}$ $\frac{???}{92}$
I knew that 100 needed to shrink to 92, but I didn't know what to use as a scale factor. I tried 100 ÷ 92, but I got 1.1 and that didn't make any sense.
Teacher: Why not?
Student: Because multiplying 100 x 1.1 will give me a bigger answer, and I need to shrink 100 to 92.
Teacher: Good reasoning. What did you do next?
Student: I tried 92 ÷ 100 and got 0.92.
Teacher: Yes. 92 ÷ 100 is the same as 92/100, which can also be written as 0.92.
Student: Then I tried 0.92 as a scale factor to see if it worked, and it did. 100 x 0.92 is 92, so I multiplied 12 x 0.92 and got 11. I think 11 of the 92 students will eat cheese pizza.
Teacher: Let me see if I understand what you did.
$\frac{12\times 0.92}{100\times 0.92}=\frac{11}{92}$
Is this accurate?
Student: Yes. And look, $\frac{0.92}{0.92}$ = 1. That's why the fractions are equivalent. I really just multiplied by 1.
Teacher: Good observation.
Student: I got 11, too, but solved the problem a different way.
Teacher: What did you do?
Student: We want to find 12% of 92. 12% is the same as 0.12, so I multiplied 0.12 x 92 and got 11.04.
Teacher: How did you know to multiply?
Student: Well, I know that 25% is 0.25 or $\frac{1}{4}$. I can find 25% of 100 by multiplying 0.25 X 100 or $\frac{1}{4}$ x 100. This is the same kind of problem, only with different numbers.
Teacher: Yes, it is. Since you can find 25% of 100 by multiplying 0.25 x 100, then you can find 12% of 92 by multiplying 0.12 x 92. Does anyone else have a different method to find 12% of 92?
Student: I was able to figure out the answer by finding 10% and 1% of 92.
Teacher: Tell me more.
Student: Well, 10% is the same as $\frac{1}{10}$ It is a scale factor that shrinks a number by one place value, so 10% of 92 is 9.2. 1% is the same as $\frac{1}{100}$. It is a scale factor that shrinks a number by two place values, so 1% of 92 is 0.92. The problem asks to find 12% of 92. 12% is 10% + 1% + 1%, so I added 10% of 92 + 1% of 92 + 1% of 2.
9.2 + 0.92 + 0.92 = 11.04, the same answer as others got.
Teacher. Right on! Another excellent strategy! I have one last question for you. The student council surveyed 25 students out of the 92 in the sixth grade. How can we determine what percent of sixth graders were surveyed?
Student: That's a tough one. When I write 25 out of 92 as a fraction, it's not easy to make an equivalent fraction with 100 as the denominator.
Student: Yeah, the numbers aren't pretty. What if we changed the fraction $\frac{25}{92}$ to a decimal?
Teacher: And how would you do that?
Student: By dividing 25 by 92. You get 0.27173913.
Teacher: What does that mean?
Student: That it's a little over 27%.
Teacher: How do you know?
Student: Percent is out of 100, so it's like hundredths. 25 divided by 92 is 27.173913 hundredths.
Teacher: A little more than 27% seems like a reasonable answer to me because 25% is 25 out of 100, and in this case we have 25 out of 92. Since 92 is less than 100, we have a bigger part. Oh, all this talking about pizza has made me hungry. It's a good thing it's lunch time. See you tomorrow!
Resources
Teacher Notes
- The word "cent" means one hundred, so "percent" means per one hundred. The symbol for percent is %.
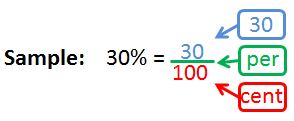
- It is essential that students recognize equivalencies and can convert among fractions, decimals, and percents. Students will need multiple opportunities to practice conversions and connect fractions, decimals, and percent equivalencies with visual models.
- Students have little difficulty writing percents as a fraction. Writing fractions as percents is more challenging. Use writing prompts, such as "To write a fraction as a percent...," to assess understanding.
- Many struggle with the meaning of the percent symbol. Some may believe that 2.4% is the same as 2.4, while others think that 0.4 is the same as 4% Remind students that when the percent is given, for instance 40%, the percent symbol (%) means writing the number as a fraction with a denominator of 100. Therefore, 40% is $\frac{40}{100}$ (which can be simplified to $\frac{2}{5}$) = 0.40. Using the same idea, 2.4% is the same as $\frac{2.4}{100}$ = $\frac{2.4}{100}\times \frac{10}{10}$ = $\frac{2.4\times 10}{100\times 100}$ = $\frac{24}{1000}$ (which can be simplified to $\frac{3}{125}$) = 0.024.
- Students that recognize $\frac{1}{10}$ as 10% may believe that $\frac{1}{5}$ is 5%. This misconception can be addressed by asking students to find equivalent fractions for $\frac{1}{10}$ and $\frac{1}{5}$ with denominator 100. This will help them to recognize that $\frac{1}{5}$ is actually 20%;
- Translating fractions such as $\frac{7}{8}$ to percents is especially challenging to students. Most understand that it is necessary to first divide the numerator of the fraction by the denominator to get the decimal (7 ÷ 8 = 0.875). At this point, confusion sets in for some as they struggle to understand next steps. Should the decimal point be moved? If so, how many places? Which direction? Encourage struggling students to rewrite the decimal as a fraction ($\frac{875}{1000}$). Remind them that percent means "out of 100," so the denominator needs to be scaled back to 100.
$\frac{875}{1000}\div\frac{10}{10}= \frac{875\div 10}{1000\div 10}=\frac{87.5}{100}=87.5%$.
- Have students create a graphic organizer that can be used to assist with translating among fractions, decimals, and percents.
- Students must understand that the percent symbol (%) signals a special ratio that compares a number to 100. In order to multiply, it is necessary to express percents as either fractions or decimals before performing the calculation.
- It is common for students to believe that increasing and then decreasing the result by the same percentage results in the original number. This misconception provides an excellent opportunity for class investigation and discussion. For example: Suppose we increased $100 by 15% then decreased by the same 15%.
Would we end up with $100?
$100 + (15% of 100) = $100 + (0.15 x 100)
= $100 + $15
= $115
Next, we would reverse the process.
$115 - (15% of 115) = $115 - (0.15 x 115)
= $115 - $17.25
= $97.75
- Percent bars are useful to help students estimate answers for finding percent of a number.
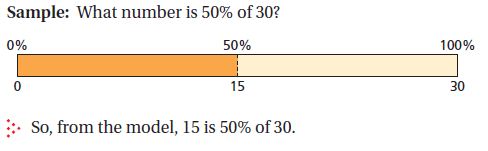
The percent bar shown above could also be used to estimate problems such as 75% of 30 or 6% of 30.
- Percent bars can also be used to estimate what percent one number is of another.
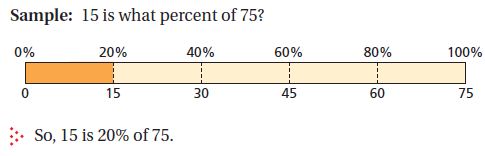
In this lesson, students use a 10 x 10 grid as a model to solve types of percent problems.
In these two lessons, students participate in activities in which they develop number sense in and around the shopping mall. The first lesson is appropriate for grades 3-5, while the second lesson is appropriate for grades 6-8. Both grade-level activities deal with size and space, estimation, measurement, and applications involving percent.
In this lesson, students purchase the common items in the mathematics classroom such as desks, chairs, calculators, manipulatives, etc. They are given a budget that they must work within and coupons they must use when making purchases.
Additional Instructional Resources
In this interactive lesson on percent, students convert fractions to percentages, work with a hundredths grid, and solve problems involving percents.
per: for each, or for every; often used with units to express a rate. Example: If apples cost $1.99 per pound, then each pound of apples costs $1.99.
percent (%): per hundred, or out of 100. Example: "12% of sixth grade students are left-handed" means that out every 100 sixth grade students, 12 are left-handed
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What evidence shows that students can fluently translate among fractions, decimals, and percents?
- How can pictorial representations of percent problems be used to scaffold students toward abstract representations?
- What everyday student experiences can be used as a source of rich problems involving percents?
- What evidence exists to show that students can find the percent of a number?
- What evidence exists to show that students can find what percent one number is of another?
Materials - suggested articles and books
Cramer, Kathleen. "Dividing Fractions and Problem Solving." Mathematics Teaching in the Middle School Feb. 2010: 338-347. Print.
Kaput, J. (1989). Linking representations in the symbol system of algebra. In C. Kieran & S.Wagner (Eds.), A research agenda for the learning and teaching of algebra. Hillsdale, NJ: Lawrence Erlbaum.
Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
South Carolina State Department of Education. Math Curriculum Standards. N.p., n.d. Web. 1 Apr. 2011. <http://ed.sc.gov/agency/Standards-and-Learning/Academic-Standards/old/c…;.
Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
National Council of Teachers of Mathematics. (2010). Focus in grade 6 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics, Inc.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
NJ Mathematics Curriculum Framework. The official web site for the state of New Jersey. N.p., n.d. Web. 1 Apr. 2011. <http://www.state.nj.us/education/frameworks/math/>.
Assessment
(DOK Level 1)
1. Find 80% of 45.
Answer: 36
(DOK Level 1)
2. A student correctly answered 15 out of 20 questions correct on a math quiz. What percent of the questions were answered correctly?
a) 15% b) 60% c) 75% d) 95%
Answer: c
(DOK Level 2)
3. A pair of running shoes is on sale for 25% off the original price.

Which price is closest to the sale price of the running shoes?
a) $93 b) $99 c) $124 d) $14
Answer: a
(DOK Level 2)
4. You went to the mall with $80 and spent $52. What percent was not spent?
Answer: 35%
(DOK Level 3)
5. Ashley plans to purchase an item that costs $20 before tax is added. Minnesota's tax rate is 6.5%. What will Ashley's total cost for the item be, including sales tax? Explain how you found your answer.
Sample Answer: Ashley's total cost will be $21.30.
The sales tax is 6.5% of $20. To find the amount of sales tax, I changed 6.5% to a decimal and multiplied it by 20.
6.5% = $\frac{6.5}{100}=\frac{6.5}{100}\times \frac{10}{10}=\frac{6.5\times 10}{100\times 10}=\frac{65}{1000}$ = 0.065
0.065 x $20 = $1.30 (sales tax)
Total cost = $20 + $1.30 = $21.30
(DOK Level 4)

6. Brigette's ice cream cone contains 16 grams of saturated fat. This is 80% of her total daily allowance. What is Brigette's total daily allowance of saturated fat in grams? Explain how you found your answer.
Sample Answer: 20 grams
80% = $\frac{80}{100}$ = $\frac{4}{5}$
If 16 grams is 80% of her total daily allowance, then 16 grams represents 4 parts out of 5. Since 16 ÷ 4 = 4, then each part is 4 grams. There are 5 parts in the total daily allowance. 4 x 5 = 20, so the total daily allowance is 20 grams.
Differentiation
- Percent
This interactive applet illustrates percent and translates among fractions, decimals, and percents.
- Have students create a graphic organizer that can be used to assist with translating among fractions, decimals, and percents;

- Percent bars are helpful to help students estimate answers for finding percent of a number.
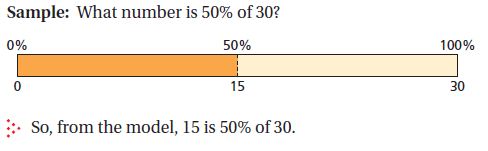
The percent bar shown above could also be used to estimate problems such as 75% of 30 or 6% of 30.
- Percent bars can also be used to estimate what percent one number is of another.
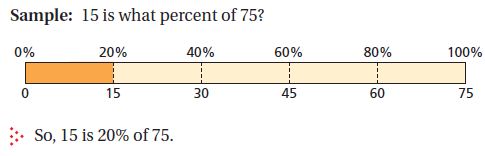
- Shopping Mall Math
In these two lessons, students participate in activities in which they develop number sense in and around the shopping mall. The first lesson is appropriate for grades 3-5, while the second lesson is appropriate for grades 6-8. Both grade-level activities deal with size and space, estimation, measurement, and applications involving percent.

In this series of three hands-on activities, students develop and reinforce their understanding of hundredths as fractions, decimals, and percentages. Students explore with candy pieces as they physically make and connect a set and linear model (meter) to produce area models (grids and pie graph).
- Ask students to find as many uses of percent within the school setting as they can find over the course of a week. Likely entries in the resulting list are grades on tests, foul shot success of the basketball team, and a measure of how close the PTA is to their fund-raising goal for the new playground equipment, and so on.
- Provide a multiplication chart to assist students who are struggling with basic multiplication facts, while encouraging them to master the facts.
- The word "cent" means one hundred, so "percent" means per one hundred. Connect the meaning of percent to words that students may have heard in other situations.

- Percent bars are helpful to help students estimate answers for finding percent of a number.
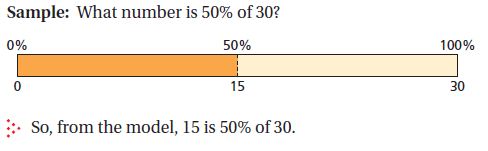
The percent bar shown above could also be used to estimate problems such as 75% of 30 or 6% of 30.
- Percent bars can also be used to estimate what percent one number is of another.
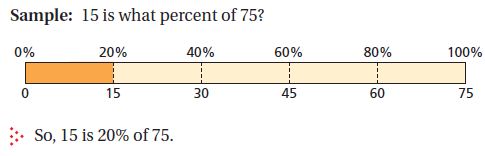
- Use graphic organizers such as the Frayer model shown below, for vocabulary development.
Big Math and Fries
In this lesson, students calculate the percent of calories from fat, carbohydrates, and protein in a daily diet.
Students can solve a variety of real-world money problems
Examples:
- If you make $750.00 a month, would you rather have a 12% raise or an $85 a month raise?
- Answer: 12% as the raise would be $90 vs. $85
Which sale is better on a $17.00 sweater, a $\frac{1}{3}$ off sale, a $5.00 discount, or a 30% discount?
- Answer: $\frac{1}{3}$ off sale as the discount will be $5.61 vs. $5 or $5.10
Is it better for a customer to take a discount of 20% and then add a 6% sales tax or add the sales tax and then take a 20% discount?
- Answer: The have the same result.
Parents/Admin
Administrative/Peer Classroom Observation
Students are: (descriptive list) | Teachers are: (descriptive list) |
understanding that percent is a ratio to 100 and converting it to a fraction or decimal. | providing students with ample opportunities to practice converting among fractions, decimals, and percents. |
using visual representations, such as percent bars, to estimate answers for percent problems. | connecting visual representations of percent problems to abstract representations. |
using fractions and decimals to calculate the percent of a number. | using students' everyday experiences as a rich source of problems. |
determining what percent one number is of another. | posing problems that require students to determine a percentage. |
using multiple strategies to solve problems involving percent in a variety of contexts. | modeling a variety of strategies that scaffolds students' understanding to more efficient strategies. |
solving meaningful and relevant percent problems; | designing lessons and activities that will engage students; |
checking answers for reasonableness. | asking students whether their answers make sense in the context of the problem. |
discussing and writing about their thinking. | requiring students to communicate their reasoning. |
valuing the usefulness of mathematics. | using the real-world as a rich source of problems. |
