3.1.2B Multiplication & Division
Represent multiplication facts by using a variety of approaches, such as repeated addition, equal-sized groups, arrays, area models, equal jumps on a number line and skip counting. Represent division facts by using a variety of approaches, such as repeated subtraction, equal sharing and forming equal groups. Recognize the relationship between multiplication and division.
Solve real-world and mathematical problems involving multiplication and division, including both "how many in each group" and "how many groups" division problems.
Use strategies and algorithms based on knowledge of place value, equality and properties of addition and multiplication to multiply a two- or three-digit number by a one-digit number. Strategies may include mental strategies, partial products, the standard algorithm, and the commutative, associative, and distributive properties.
For example: 9 × 26 = 9 × (20 + 6) = 9 × 20 + 9 × 6 = 180 + 54 = 234
Overview
Standard 3.1.2 Essential Understandings
Students build on previous work with addition and subtraction of 2-digit numbers to include multi-digit whole number addition and subtraction. They use various strategies to solve real-world and mathematical problems involving addition and subtraction.
Third grade students begin their formal work with multiplication and division by representing basic facts in a variety of ways.
They represent multiplication facts in a variety of ways including:
- repeated addition
- equal groups
- arrays
- equal jumps on a number line (skip counting)
They represent division facts in a variety of ways including:
- repeated subtraction
- equal sharing
- forming equal groups
Students develop an understanding of the relationship between multiplication and division which will lead to the development of a variety of strategies for multiplying and dividing. They will solve real-world and mathematical problems involving multiplication and division. Problem solving involving division will include both "how many in each group" and "how many groups" problems.
Multiplication extends to multiplying a two- or three-digit number by a one-digit number. Strategies may include mental strategies, partial products, the standard algorithm, and the commutative, associative and distributive properties. Strategic thinking when solving problems is the focus, not procedures.
Benchmark Group B
3.1.2.3: Represent multiplication facts by using a variety of approaches, such as repeated addition, equal-sized groups, arrays, area models, equal jumps on a number line and skip counting. Represent division facts by using a variety of approaches, such as repeated subtraction, equal sharing and forming equal groups. Recognize the relationship between multiplication and division.
3.1.2.4: Solve real-world and mathematical problems involving multiplication and division, including both "how many in each group" and "how many groups" division problems.
3.1.2.5: Use strategies and algorithms based on knowledge of place value and properties of addition and multiplication to multiply a two- or three-digit number by a one-digit number. Strategies may include mental strategies, partial products, the standard algorithm, and the commutative, associative, and distributive properties.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Demonstrate an understanding of multiplication being how many groups times how many in a group.
- Demonstrate multiplicative thinking by understanding that multiplication involves. counting groups of like size and determining how many there are in all.
- Understand that multiplication and division are related and inverse operations.
- Demonstrate an understanding of multiplication as repeated addition and division as repeated subtraction.
- Complete multiplication and division problems using a variety of strategies including: repeated addition, constructing arrays, breaking apart two- or three-digit times one-digit multiplication problems to solve, using repeated subtraction.
- Use knowledge/skills of one-digit multiplication to complete two- or three-digit by one digit multiplication problems.
- Group objects in rows and columns or use manipulatives to form an array in completing a multiplication problem.
- Separate objects into groups either by drawing or using manipulatives to complete a division problem.
- Solve division problems involving How many in each group? and How many groups?
- Recognize the concept of multiples of numbers (i.e. 6, 9, 12 are multiples of three and the same as multiplying 3 x 2, 3 x 3, and 3 x 4).
Work from previous grades that supports this new learning includes:
- Use a variety of strategies to solve problems.
- Use base-ten blocks to complete problems by grouping in ones, tens and hundreds.
- Round numbers to the nearest 10, 100 and add the rounded numbers.
- Understand place value up to but not including the thousands place.
- Understand the concept of adding and subtracting.
- Know basic addition and subtraction facts.
- Complete rep.
NCTM Standards
Understand meanings of operations and how they relate to one another
Grades 3 - 5 Expectations
- understand various meanings of multiplication and division;
- understand the effects of multiplying and dividing whole numbers;
- identify and use relationships between operations, such as division as the inverse of multiplication, to solve problems;
- understand and use properties of operations, such as the distributivity of multiplication over addition.
Compute fluently and make reasonable estimates
Grades 3 - 5 Expectations
- develop fluency with basic number combinations for multiplication and division and use these combinations to mentally compute related problems, such as 30
Misconceptions
Students may think...
- they should add when seeing the multiplication symbol.
- additively rather than multiplicatively. They may not see problems in terms of the number of groups and the number in each group.
- the commutative property of multiplication applies to division
- multiplication functions the same way as addition. For example, multiplying by 0 means nothing changes and multiplying by 1 means getting 1 more
- 2 x 7 and 7 x 2 are two separate facts and need to be learned independently. They are unable to apply the commutative property of multiplication when learning basic facts.
Resources
Teacher Notes
- Students may need support in further development of previously studied concepts and skills.
- Students need to see multiplication represented in a variety of ways: repeated addition, an array model, and a groups of model.
- Students need to see multiple representations of division: repeated subtraction, sets of objects being divided into equal size groups, or into a groups of a specified size.
- Time tests are not an effective strategy for fact acquisition. "...asking students to demonstrate this knowledge [basic facts] within an arbitrary time limit may actually interfere with their learning." (Seeley, 2009, pg.93)
- Basic fact knowledge is not about memorization. It is about being able to derive an unknown fact from a known fact or using other thinking strategies. "All of the facts are conceptually related. You can figure out new or unknown facts from those you already know." (Van de Walle & Lovin, 2006, p.94)
- Students need strategies for deriving multiplication facts. Many of these strategies use the associative and distributive properties. Although facts do not need to be learned in any particular order, here are some strategies students use when deriving facts.
- Relate multiplying by 2 to addition doubles.
- Relate multiplying by 3 to doubling and adding one more set.
- Ex. 3 x 8 is the same as (2 x 8) + 8
- Relate multiplying by 4 to doubling and doubling again.
- Relate multiplying by 5 to skip counting by five.
- Relate multiplying by 6 to multiplying by 3 and .
- Relate multiplying by 7 to using known facts.
- Ex. 7 x 8 is the same as (5 x 8) + (2 x 8).
- Relate multiplying by 8 to multiplying by 4 and then doubling.
- Relate multiplying by 9 to multiplying by 10 and subtracting one set.
- Ex. 9 x 8 is the same as (10 x 8) - 8.
- Relate multiplying by 10 to place value knowledge of groups of ten.
- Student understanding and use of the commutative property reduces the number of multiplication facts from 100 to 55.
- Understanding the relationship between multiplication and division aids in learning basic facts. Teachers need to make this relationship visible as students develop basic fact knowledge. For example, 12 divided by 4 equals 3 because 4 times 3 equals 12. The array for 4 times 3 is the same as the array for 12 objects being put into 4 rows.
- Fact Triangles are tools used to help build mental arithmetic skills. Fact Triangles are effective for helping students memorize facts because of their emphasis on relationships in a fact family.
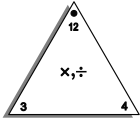
A fact family is a collection of four related facts linking two inverse operations. For instance, the following four equations represent the fact family relating 3, 4, and 12 with multiplication and division.
4 x 3 = 12 12 ÷ 4 = 3 3 x 4 = 12 12 ÷ 3 = 4
To use the Fact Triangles,
- ask students to write or say the four equations that represent the fact family for the numbers on the card
- cover one of the numbers and ask students to identify the missing number for the fact family. Once the missing number has been identified, students can write all four equations for the fact family.

- Students need to solve division problems involving equal groups.
Equal Group Division Types:
Partitive Division - How many in each group?
The total number of objects is partitioned into a specified number of groups. For example, you have 27 people and 9 tables.
If each table seats the same number of people, how many people will you put at each table?
Measurement Division - How many groups?
The total number of objects is measured out into groups of a certain size. For example, If you have 27 people and tables that will hold 9 people, how many tables will you need.
- Modeling word problems is critical as students develop an understanding of operations and the relationships that exist between and among those operations. The bar model is an effective tool that can be used to represent the relationships in a variety of problem solving situations.
- Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if...?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to...?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work? Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part ...
(Adapted from They're Counting on Us, California Mathematics Council, 1995)
- Lessons for Multiplication: In this unit, students explore several meanings and representations of multiplication (number line, equal sets, arrays, and balanced equations). They also learn about the order (commutative) property of multiplication, the results of multiplying by 1 and by 0, and the inverse property of multiplication. In addition, students write story problems in which the operation of multiplication is required. Opportunities to connect with literature are presented in several of the lessons.
- Multiply and Conquer: Students decompose 2-digit numbers, model area representations using the distributive property and partial product arrays, and align paper-and-pencil calculations with the arrays. The lessons provide conceptual understanding of what occurs in a 2-digit multiplication problem. Partial product models serve as transitions to understanding the standard multiplication algorithm. For third graders, use the 2 x 1 Multiplication Arrays.
Additional Instructional Resources
Burns, M.. (2001). Teaching arithmetic: Lessons for introducing multiplication, grades 3. Sausalito, CA: Math Solutions.
Duncan, N., Geer, C., Huinker, D., Leutzinger, L., Rathmell, E., & Thompson, C. (2007). Navigating through number and operations in grades 3-5. Reston, VA: National Council of Teachers of Mathematics.
Fosnot, C., & Dolk, M. (2002). Young mathematicians at work: Multiplication and division. Portsmouth, NH: Heinemann
Murray, M. (2004) Teaching Mathematics Vocabulary in Context. Portsmouth, NH: Heinemann.
O'Connell, S., & SanGiovanni, J.. (2011). Mastering the basic math facts multiplication and division strategies, activities & interventions to move students beyond memorization. Portsmouth, NH: Heinemann.
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Uittenbogaard, W., Fosnot, C. (2008). Minilessons for early multiplication and division, Grades3-4. Portsmouth, NH: Heinemann.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.) Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades 3-5. Boston, MA: Pearson Education.
Wickett, M., Ohanian, S.,& Burns, M., (2002). Teaching arithmetic: lessons for introducing division, grades 3-4. Sausolito, CA: Math Solutions.
Yeatts, K., Battista, M., Mayberry, S., Thompson, D., & Zawojewski, J. (2004). Navigating through problem solving and reasoning in grade 3. Reston, VA: National Council of Teachers of Mathematics.
New Vocabulary
multiply: to add the same quantity many times
factors: two numbers that are multiplied together to obtain a product
divide: an operation to find how many groups and how many in each group
dividend: the number being divided
divisor: the number by which another number is divided
product: the answer in a multiplication problem
quotient: the answer in a division problem
"Vocabulary literally is the key tool for thinking."
Ruby Payne
Mathematics vocabulary words describe mathematical relationships and concepts and cannot be understood by simply practicing definitions. Students need to have experiences communicating ideas using these words to explain, support, and justify their thinking.
Learning vocabulary in the mathematics classroom is contingent upon the following:
Integration: Connecting new vocabulary to prior knowledge and previously learned vocabulary. The brain seeks connections and ways to make meaning which occurs when accessing prior knowledge.
Repetition: Using the word or concept many times during the learning process and connecting the word or concept with its meaning. The role of the teacher is to provide experiences that will guarantee connections are made between mathematical concepts, relationships, and corresponding vocabulary words.
Meaningful Multiple and varied opportunities to use the words in context. These
Use: opportunities occur when students explain their thinking, ask clarifying questions, write about mathematics, and think aloud when solving problems. Teachers should be constantly probing student thinking in order to determine if students are connecting mathematics concepts and relationships with appropriate mathematics vocabulary.
Strategies for vocabulary development
Students do not learn vocabulary words by memorizing and practicing definitions. The following strategies keep vocabulary visible and accessible during instruction.
Mathematics Word Bank: Each unit of study should have word banks visible during instruction. Words and corresponding definitions are added to the word bank as the need arises. Students refer to word banks when communicating mathematical ideas which leads to greater understanding and application of words in context.
Labeled pictures and charts: Diagrams that are labeled provide opportunities for students to anchor their thinking as they develop conceptual understanding and increase opportunities for student learning.
Frayer Model: The Frayer Model connects words, definitions, examples and non-examples.
Example/Non-example Charts: This graphic organizer allows students to reason about mathematical relationships as they develop conceptual understanding of mathematics vocabulary words. Teachers should use these during the instructional process to engage student in thinking about the meaning of words.

Vocabulary Strips: Vocabulary strips give students a way to organize critical information about mathematics vocabulary words.
|
word |
definition |
illustration |
Encouraging students to verbalize thinking by drawing, talking, and writing increases opportunities to use the mathematics vocabulary words in context.
Additional Resources for Vocabulary Development
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Reflection - Critical Questions regarding classroom practice
What are the key ideas related to multiplication and division at the third grade level? How do student misconceptions interfere with mastery of these ideas?
What experiences do students need in order to develop an understanding of multiplication and division?
How do third graders represent multiplication and division? What strategies do third graders use in solving multiplication and division problems.
Write a division problem that would be solved using equal sharing.
Write a division problem that would be solved by forming equal groups.
When checking for student understanding of multiplication/division, what should teachers
- listen for in student conversations?
- look for in student work?
- ask during classroom discussions?
Examine student work related to a task involving multiplication or division. What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
How can teachers assess student learning related to these benchmarks?
How are these benchmarks related to other benchmarks at the third grade level?
Professional Learning Community Resources
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K.. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach, grades K-8, 2nd Edition. Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Fosnot, C., & Dolk, M.. (2002). Young mathematicians at work: multiplication and division. Portsmouth, NH: Heinemann.
Hyde, Arthur. (2006) Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Otto, A., Caldwell, J., Wallus Hancock, S., & Zbiek, R..(2011). Developing essential understanding of multiplication and division for teaching mathematics in grades 3 - 5. Reston, VA.: National Council of Teachers of Mathematics.
Parrish, S. (2010). Number talks: helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension-using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J.. (2009). Focus in grade 3, teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA: Corwin Press.
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Burns, Marilyn. (2007). About teaching mathematics: A k-8 resource (3rd ed.). Sausalito, CA: Math Solutions Publications.
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Caldera, C. (2005). Houghton Mifflin math and English language learners. Boston, MA: Houghton Mifflin Company.
Carpenter, T., Fennema, E., Franke, M., Levi, L., & Empson, S. (1999). Children's mathematics cognitively guided instruction. Portsmouth, NH: Heinemann.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Chapin, S., & Johnson, A. (2006). Math matters: Understanding the math you teach, grades K-8. (2nd ed.). Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Dacey, L., & Salemi, R. (2007). Math for all: Differentiating instruction k-2. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Dougherty, B., Flores, A., Louis, E., & Sophian, C. (2010). Developing essential understanding of number & numeration pre-k-grade 2. Reston, VA: National Council of Teachers of Mathematics.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Fuson, K., Clements, D., & Beckmann, S. (2009). Focus in grade 2 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, Arthur. (2006). Comprehending math adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
O'Connell, S., & SanGiovanni, J. (2011). Mastering the basic math facts multiplication and division strategies, activities & interventions to move students beyond memorization. Portsmouth, NH: Heinemann
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J., Charles, R., Clements, D., Duckett, P., Fennell, F., Lewandowski, S., ... & Zbiek, R. M. (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: A quest for coherence. Reston, VA: NCTM.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Uittenbogaard, W., & Fosnot, C. (2008). Mini-lessons for early multiplication and division, Grades 3-4. Portsmouth, NH: Heinemann.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J. A., & Lovin, L. H. (2006). Teaching student-centered mathematics grades K-3. Boston, MA: Pearson Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
Wickett, M., Ohanian, S., & Burns, M. (2002). Teaching arithmetic: Lessons for introducing division, Grades 3-4. Sausalito, CA: Math Solutions.
Yeatts, K., Battista, M., Mayberry, S., Thompson, D., & Zawojewski, J. (2004). Navigating through problem solving and reasoning in grade 3. Reston, VA: National Council of Teachers of Mathematics.
Zemelman, S., Daniels, H., & Hyde, A. (2005). Best practices: Today's standards for teaching and learning in America's schools. Portsmouth, NH: Heinemann.
Assessment
- Malik has 64 marbles.
He puts an equal number of marbles into each of 4 jars.
How many marbles are in each jar?
A. 14
B. 15
C. 16
D. 18
Solution: C. 16
Benchmark: 3.1.2.3, 3.1.2.4
MCA III item sampler
- Multiply. 507× 6
A. 342
B. 3,002
C. 3,042
D. 3,102
Solution: C. 3,042
Benchmark: 3.1.2.5
MCA III item sampler
- Which story problem can be solved using the number sentence 2 X n = 18?
A. Tom had 18 pencils. He gave n pencils away and had 2 left over. How many pencils did Tom give away?
B. Alice bought n books and spent $18. Each book cost $2. How many books did Alice buy?
C. Maya had n rocks and 2 baskets. She put 18 rocks in each basket. How many rocks did Maya have?
D. Pedro saw 2 kinds of birds. He saw 18 robins and n crows. How many crows did Pedro see?
Solution: B
Benchmark: 3.1.2.3, 3.1.2.4
MCA III item sampler
- During class, 16 students were divided into 8 different groups. How many students were in each group?
A. 24
B. 3
C. 128
D. 2
Solution: D. 2
Benchmark: 3.1.2.3, 3.1.2.4
MCA III item sampler
- There are 56 students on the math team. If they are sitting 8 students in a row, how many rows will they need?
A. 64
B. 12
C. 7
D. 6
Solution: C. 7
Benchmark: 3.1.2.3, 3.1.2.4
MCA III item sampler
- Joe has 8 packs of Life Savers Candy. Each pack contains 5 pieces of candy. If Joe eats 3 pieces, how many pieces does he have left?
A. 37
B. 32
C. 13
D. 8
Solution: A. 37
Benchmark: 3.1.2.3, 3.1.2.4
MCA III item sampler
- The answer is 42. What is the multiplication or division question?
Solution: 6 X 7, 84![]() 2
2
Benchmark: 3.1.2.3, 3.1.2.4, 3.1.2.5
MCA III item sampler
Differentiation
Students who remain emergent in their understanding of multiplication and division need to use manipulatives to make sense of the operations. The groups of model and the array model of are effective representations for emergent learners.
- Fact Triangles are tools used to help build mental arithmetic skills. Fact Triangles are effective for helping students memorize facts because of their emphasis on relationships in a fact family.

A fact family is a collection of four related facts linking two inverse operations. For instance, the following four equations represent the fact family relating 3, 4, and 12 with multiplication and division.
4 x 3 = 12 12 ÷ 4 = 3 3 x 4 = 12 12 ÷ 3 = 4
To use the Fact Triangles,
- ask students to write or say the four equations that represent the fact family for the numbers on the card
- cover one of the numbers and ask students to identify the missing number for the fact family. Once the missing number has been identified, students can write all four equations for the fact family.

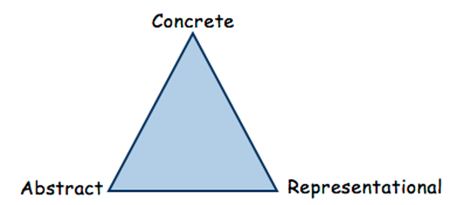
Concrete - Representational - Abstract Instructional Approach
The Concrete-Representational-Abstract Instructional Approach (CRA) is a research-based instructional strategy that has proven effective in enhancing the mathematics performance of students who struggle with mathematics.
The CRA approach is based on three stages during the learning process:
Concrete - Representational - Abstract
The Concrete Stage is the doing stage. The concrete stage is the most critical in terms of developing conceptual understanding of mathematical skills and concepts. At this stage, teachers use manipulatives to model mathematical concepts. The physical act of touching and moving manipulatives enables students to experience the mathematical concept at a concrete level. Research shows that students who use concrete materials develop more precise and comprehensive mental representations, understand and apply mathematical concepts, and are more motivated and on-task. Manipulatives must be selected based upon connections to the mathematical concept and the students' developmental level.
The Representational Stage is the drawing stage. Mathematical concepts are represented using pictures or drawings of the manipulatives previously used at the Concrete Stage. Students move to this level after they have successfully used concrete materials to demonstrate conceptual understanding and solve problems. They are moving from a concrete level of understanding toward an abstract level of understanding when drawing or using pictures to represent their thinking. Students continue exploring the mathematical concept at this level while teachers are asking questions to elicit student thinking and understanding.
The Abstract Stage is the symbolic stage. Teachers model mathematical concepts using numbers and mathematical symbols. Operation symbols are used to represent addition, subtraction, multiplication and division. Some students may not make a clean transfer to this level. They will work with some symbols and some pictures as they build abstract understanding. Moving to the abstract level too quickly causes many student errors. Practice at the abstract level will not lead to increased understanding unless students have a foundation based upon concrete and pictorial representations.
Additional Resources:
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms!. Thousand Oaks, CA: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades 3-5. Sausalito, CA: Math Solutions.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
O'Connell, S., & SanGiovanni, J..\ (2011). Mastering the basic math facts multiplication and division strategies, activities & interventions to move students beyond memorization. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: Teaching developmentally. (7th ed.). Boston, MA: Allyn & Bacon.
Van de Walle, J., & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades 3-5. Boston, MA: Pearson Education.
- Students may need clarification of vocabulary used in story problems.
- Students should demonstrate an understanding of a story problem by explaining the problem in their own words before choosing a solution strategy.
- Students need to use manipulatives to make sense of the operations. The groups of model and the array model of are effective representations.
- Students should explain their strategy for solving a problem. Using manipulatives may help in clarifying student thinking.
- Word banks need to be part of the student learning environment in every mathematics unit of study.
- Word Use vocabulary graphic organizers such as the Frayer model (see below) to emphasize vocabulary words count, first, second, third, etc.
- Sentence Frames
Math sentence frames provide support that English Language Learners need in order to fully participate in math discussions. Sentence frames provide appropriate sentence structure models, increase the likelihood of responses using content vocabulary, help students to conceptualize words and build confidence in English Language Learners.
Sample sentence frames related to these benchmarks:
|
There are ________ groups of _________. That makes____________. |
|
There are ______ total put into _________ groups so each group has _______________. |
- When assessing the math skills of an ELL student it is important to determine if the student has difficulty with the math concept or with the language used to describe the concept and conceptual understanding.
Additional ELL Resources:
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Students solve multiplication word problems involving two- and three-digit by one digit and explain solution strategies.
Students use at least two methods in solving a problem involving multiplication. The strategies are then compared and contrasted.
Additional Resources
Bender, W. (2009). Differentiating math instruction-strategies that work for k-8 classrooms! Thousand Oaks, CA: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: differentiating instruction grades 3-5. Sausalito, CA: Math Solutions.
Murray, M., & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are... |
Teachers are... |
|
using arrays and area models to represent multiplication and division and explaining what the models represent.
|
incorporating multiple representations for multiplication and division and asking students to explain the representations.
|
|
sharing solution strategies and justifying their thinking when solving a problem.
|
using correct mathematics vocabulary when eliciting responses form students. Defining terms should be woven throughout the lesson.
|
|
using more than one strategy to solve any given problem and explaining their strategies. |
comparing and contrasting student strategies to further student understanding while facilitating the use of more efficient strategies. |
|
connecting multiplication to repeated addition. |
keeping the connection between multiplication and repeated addition visible. |
|
connecting division to repeated subtraction. |
keeping the connection between division and repeated subtraction visible. |
What should I look for in the mathematics classroom?
(Adapted from SciMathMN,1997)
What are students doing?
- Working in groups to make conjectures and solve problems.
- Solving real-world problems, not just practicing a collection of isolated skills.
- Representing mathematical ideas using concrete materials, pictures and symbols. Students know how and when to use tools such as blocks, scales, calculators, and computers.
- Communicating mathematical ideas to one another through examples, demonstrations, models, drawing, and logical arguments.
- Recognizing and connecting mathematical ideas.
- Justifying their thinking and explaining different ways to solve a problem.
What are teachers doing?
- Making student thinking the cornerstone of the learning process. This involves helping students organize, record, represent, and communicate their thinking.
- Challenging students to think deeply about problems and encouraging a variety of approaches to a solution.
- Connecting new mathematical concepts to previously learned ideas.
- Providing a safe classroom environment where ideas are freely shared, discussed and analyzed.
- Selecting appropriate activities and materials to support the learning of every student.
- Working with other teachers to make connections between disciplines to show how math is related to other subjects.
- Using assessments to uncover student thinking in order to guide instruction and assess understanding.
Additional Resources
For Mathematics Coaches
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach: Grades k-8, 2nd edition. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
For Administrators
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for school administrators. Reston, VA: National Council of Teachers of Mathematics.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Parent Resources
Mathematics handbooks to be used as home references:
Cavanagh, M. (2004). Math to Know: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Helping your child learn mathematics
Provides activities for children in preschool through grade 5
What should I look for in the mathematics program in my child's school? A Guide for Parents developed by SciMathMN
Help Your Children Make Sense of Math
Ask the right questions
In helping children learn, one goal is to assist children in becoming critical and independent thinkers. You can help by asking questions that guide, without telling them what to do.
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if . . . ?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to ...?
Can you make a prediction?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work?
Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part...
Adapted from They're counting on us, California Mathematics Council, 1995
Read-Aloud-Books
- Aker, S. (1990). What comes in 2's, 3's, and 4's. New York: Simon and Schuster.
- Anno, Mitsumasa, & Anno, Masaichiro. (1983). Anno's mysterious counting jar. New York: Putnam.
- Dee, R. Two ways to count to ten. (1988). New York: Henry Holt.
- Giganti, P. (1992). Each orange had eight slices. New York: Greenwillow.
- Pinczes, E. (1993). One hundred hungry ants. New York: Houghton Mifflin.
