2.1.2B Addition & Subtraction in the Real World
Estimate sums and differences up to 100.
For example: Know that 23 + 48 is about 70.
Solve real-world and mathematical addition and subtraction problems involving whole numbers with up to 2 digits.
Use mental strategies and algorithms based on knowledge of place value and equality to add and subtract two-digit numbers. Strategies may include decomposition, expanded notation, and partial sums and differences.
For example: Using decomposition, 78 + 42, can be thought of as:
78 + 2 + 20 + 20 = 80 + 20 + 20 = 100 + 20 = 120
and using expanded notation, 34 - 21 can be thought of as:
30 + 4 - 20 - 1 = 30 - 20 + 4 - 1 = 10 + 3 = 13.
Overview

Strand: Number and Operation
Standard
2.1.2 Demonstrate mastery of addition and subtraction basic facts; add and subtract one- and two-digit numbers in real-world and mathematical problems.
Standard 2.1.2 Essential Understanding
Second graders use their understanding of addition and subtraction to develop quick recall of basic facts with sums to 18 and the related subtraction facts. Quick recall of basic facts include the use of these mental strategies
- counting on and counting back
- composing and decomposing numbers (12 is the same as 8 and 4 or 7 and 5, etc)
- making a ten ( 9 + 5 = 10 + 4)
- fact families ( 7 + 6 = 13, 6 + 7 =13, 13 - 7 = 6, 13 - 6 = 7)
- doubles and doubles plus/minus one
- commutative property ( 6 + 9 = 9 + 6 )
- associative property ( 5 + 8 = (3 + 2) + 8 = 3 + (2 + 8) = 3 + 10 = 13 )
Second graders develop, understand, explain and use accurate and generalizable methods to add and subtract two-digit whole numbers. Estimating sums and differences is also included in the work with addition and subtraction. They use mental strategies and algorithms based on place value and equality to solve problems. Strategies include
- composing and decomposing numbers
- using expanded notation
- using partial sums and differences ( 47 - 23 = (40 - 20) + (7 - 3) = 20 + 4 = 24)
- applying the associative property.
All Standard Benchmarks
2.1.2.1 Use strategies to generate addition and subtraction facts including making tens, fact families, doubles plus or minus one, counting on , counting back, and the commutative and associative properties. Use the relationship between addition and subtraction to generate basic facts.
2.1.2.2 Demonstrate fluency with basic addition facts and related subtraction facts.
2.1.2.3 Estimate sums and differences up to 100.
2.1.2.4 Use mental strategies and algorithms based on knowledge of place value to add and subtract two-digit numbers. Strategies may include decomposition, expanded notation, and partial sums and differences.
2.1.2.5 Solve real-world and mathematical addition and subtraction problems involving whole numbers with up to 2 digits.
2.1.2.6 Use addition and subtraction to create and obtain information from tables, bar graphs and tally charts.
Benchmark Group B
2.1.2.3 Estimate sums and differences up to 100.
2.1.2.4 Use mental strategies and algorithms based on knowledge of place value to add and subtract two-digit numbers. Strategies may include decomposition, expanded notation, and partial sums and differences.
2.1.2.5 Solve real-world and mathematical addition and subtraction problems involving whole numbers with up to 2 digits.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- add and subtract multi-digit whole numbers by being flexible, efficient and accurate problem solvers.
- use a variety of solution strategies in problem solving situations.
- apply their understanding of models of addition and subtraction and relationships and properties of number.
- use estimation to find sums and differences
- use estimation to check the reasonableness of results.
Work from previous grades that supports this new learning includes:
- basic fact knowledge (current grade level)
- composing and decomposing numbers up to 12
- understanding of base ten place value--tens and ones
- use a variety of manipulatives to solve addition and subtraction problems in part-part-total, adding to, taking away from, and comparing situations
- recognize the relationship between counting and addition and subtraction
- skip count by 2s, 5s, and 10s
NCTM Standards
Understand meanings of operations and how they relate to one another
Pre-K - 2 Expectations
- understand various meanings of addition and subtraction of whole numbers and the relationship between the two operations;
- understand the effects of adding and subtracting whole numbers;
- understand situations that entail multiplication and division, such as equal groupings of objects and sharing equally.
Compute fluently and make reasonable estimates.
Pre-K - 2 Expectations
- develop and use strategies for whole-number computations, with a focus on addition and subtraction;
- develop fluency with basic number combinations for addition and subtraction;
- use a variety of methods and tools to compute, including objects, mental computation, estimation, paper and pencil, and calculators.
Formulate questions that can be addressed with data and collect, organize, and display relevant data to answer them
Pre-K - 2 Expectations
- pose questions and gather data about themselves and their surroundings;
- sort and classify objects according to their attributes and organize data about the objects;
- represent data using concrete objects, pictures, and graphs.
- describe parts of the data and the set of data as a whole to determine what the data show.
Select and use appropriate statistical methods to analyze data
Pre-K - 2 Expectations
- describe parts of the data and the set of data as a whole to determine what the data show.
Common Core State Standards
Represent and solve problems involving addition and subtraction.
2.OA.1. Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
Add and subtract within 20.
2.OA.2. Fluently add and subtract within 20 using mental strategies.2 By end of Grade 2, know from memory all sums of two one-digit numbers.
Work with equal groups of objects to gain foundations for multiplication.
2.OA.3. Determine whether a group of objects (up to 20) has an odd or even number of members, e.g., by pairing objects or counting them by 2s; write an equation to express an even number as a sum of two equal addends.
2.OA.4. Use addition to find the total number of objects arranged in rectangular arrays with up to 5 rows and up to 5 columns; write an equation to express the total as a sum of equal addends.
Use place value understanding and properties of operations to add and subtract.
2.NBT.5. Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
2.NBT.6. Add up to four two-digit numbers using strategies based on place value and properties of operations.
2.NBT.7. Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.
2.NBT.8. Mentally add 10 or 100 to a given number 100-900, and mentally subtract 10 or 100 from a given number 100-900.
2.NBT.9. Explain why addition and subtraction strategies work, using place value and the properties of operations.
Represent and interpret data.
2.MD.9. Generate measurement data by measuring lengths of several objects to the nearest whole unit, or by making repeated measurements of the same object. Show the measurements by making a line plot, where the horizontal scale is marked off in whole-number units.
1.MD.10. Draw a picture graph and a bar graph (with single-unit scale) to represent a data set with up to four categories. Solve simple put-together, take-apart, and compare problems1 using information presented in a bar graph.
Misconceptions
Students may think...
- it's okay to "subtract up" when the digit in the minuend is smaller than the digit in the subtrahend. For example, 56 - 37, the student may subtract 6 from 7 and get 1. Then subtract 3 from 5 and get 2, for an answer of 21.
- an estimate is the exact solution
- there is only one way to get the answer
Vignette
In the Classroom
Vignette 1
The children in Mr. O.'s second grade class have been using several different strategies for solving multi-digit addition problems. Mr. O. uses a "Bansho" wall, where children post their solutions to a common problem and then group them according to solution strategies. Mr. O. has the children use drawings and diagrams to help set up story problems. After the problem is understood and set up, children solve it in a variety of ways. These second graders have had many classroom discussions involving comparing and contrasting solution strategies for a variety of problem types. These lessons took place during the third quarter of the school year. Mr. O. regularly uses his students' names in the story problems.
Mr. O.: Today we will be solving the following problem.
Lizett had 59 rocks in her collection.
She found some more by the lake.
Now she has 83 rocks.
How many rocks did she find by the lake?
Mr. O.: Lizett, would you please read the problem for us?
Lizett reads the story problem.
Mr. O. helps the class unpack the story problem by asking the following questions
Mr. O.: What happened in this story problem?
Student: Lizett found some rocks.
Mr. O.: Tell me more . . .
Student: Lizett found more rocks for her rock collection.
Mr. O.: How many rocks does Lizett have in her rock collection?
Student: She had 59, but she got more and now she has 83.
Mr. O.: What is the question in this problem?
Student: How many rocks did she find by the lake?
Mr. O.: Who can come up and write the answer sentence for this problem?

Student writes: Lizett found ____ rocks.
Writing the answer sentence helps the students keep in mind what the problem is asking and what they are trying to determine.
Mr. O.: How are we going to figure out the answer?
Student: Well, we know she started out with 59 rocks.
Student: Yeah, then she found some more.
Mr. O.: Thank you. Ok, Class. Who can come up and draw a model for the problem?

Jerjuan: We're talking about rocks, so I wrote rocks. Then I drew a bar,
and put 59 in that part because she has 59 rocks to begin with. Then I drew another part to show the rocks she found. I don't know what the number is so I put a question mark. We have to find out what number goes in there. But I know she has 83 rocks now, so I put 83 here.
Mr. O.: Who can explain how Jerjuan's model represents the problem?
Celia: Jerjuan drew the first section to show 59 rocks Lizett had. The second part with the question mark shows the number of rocks
Lizett found at the lake. We do not know that number that is why there is a question mark in that part. The curvy line shows all the rocks Lizett has.
Mr. O.: Everyone please turn to your neighbor and explain Jerjuan's model for the problem.
Mr O.: Who will come up to write a number model for our problem?
Mr. O. has the children write a "semantic number model" first - showing what is happening in the story problem. They can choose to solve this problem by subtraction, but the story implies adding which is the first equation they write.
Sophie comes up and writes: 59 + R = 83

Mr. O.: Tell us about your equation.
Sophie: Well, it matches the model drawing. The first piece of the bar is 59 rocks. We don't know how big the other piece is so I put "R" for rocks. We know the whole bar is 83, so I put that here (after the equal sign.
Mr. O.: Why did Sophie write an addition equation?
Jon: Because Lizett had 59 rocks and got some more and now she has 83 rocks altogether. That means she added some rocks to her collection.
Mr. O.: It is now time to think about how you are going to solve the problem. You can use any strategy that works for you. Be sure to show all your work. When you are ready, solve the problem. We'll post your solutions on the Bansho Wall as you finish.
The second graders get right to work. There is a low hum in the room as the students discuss the problem and get to work. The children are seated in groups of four to six. They may work together or individually - their choice. Everyone must complete the problem and show their work.
Ray finished first and placed his solution on the Bansho Wall. Mr. O. puts a label above it that says, "Empty Number Line" to name Ray's strategy.

As other children finish, they come up to compare their strategies and then post their work. Each child is asked to look at all the work posted, then decide where to place his/her work. If it is the same method as another piece of work already posted, they put their work right underneath it. If it is a similar strategy, but used different sized jumps, or slightly different numbers, they put it to the right of the original posting. Mr. O guides the placement of the children's work so the strategies progress from least sophisticated/efficient, to more sophisticated and efficient strategies. He also facilitates discussions regarding similarities and differences between solution strategies.

Strategies the children used on this problem were:
Empty Number Line
to count on
to count back
Series of Equations
to count on
to count back
Partial Differences
Compensation
Base 10 Blocks
When all the children have posted their work on the wall, Mr. O. guides a whole group discussion about the strategies.
Mr. O.: What do you notice about the solution strategies we have posted
for this problem?
Student: There are five different ways up there.
Mr. O.: What do you notice about the groupings of the strategies?
Student: A lot of kids like to use the empty number line.
Mr. O.: How do you know?
Student: There are more papers there.
Mr. O.: Good observation. What else do you notice?
Student: I like the way Supha changed the numbers before he subtracted to make it easier to do.
Mr. O.: How did he change the numbers?
Student: Well, he added 3 to the 57 to make 60 and 3 to the 83 to make 86. Then his problem was 86 - 60 which is easy to do.
Mr. O.: Why did he add the same amount to both 57 and 83?
Student: Because when you subtract you want to find the difference between the numbers. That's the same as the distance between them on the number line. So, if you change one number, you have to change the other number the same way to keep the distance between them the same.
Mr. O.: Nice explanation. Thank you. Cassie, would you please explain how you solved the problem?
Cassie: Well, I put out Base 10 blocks to show 57.
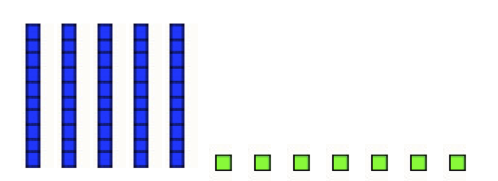
Mr. O.: What do the Base 10 blocks represent?
Cassie: Those are the rocks she already had.
Mr. O.: So, what did you do next?
Cassie: I put out more Base 10 blocks.
Mr. O.: How did you know how many more to put out?
Cassie: Well, I counted on 'til I got to 83.
Mr. O.: How did you count?
Cassie: Well, I had 57 and then put out longs and counted by 10s - 67, 77 and I knew 87 would be too many, so I counted on by ones -
78, 79, 80, 81, 82, 83.
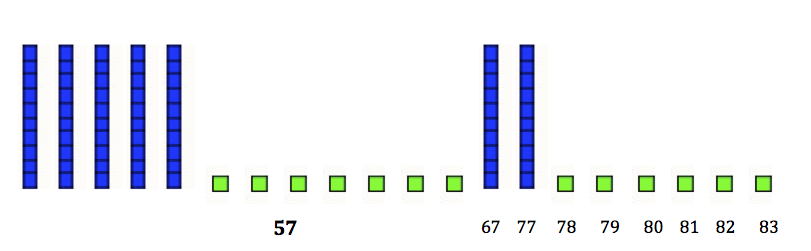
Mr. O.: So, how many blocks did you add on?
Cassie: I kept them kind of separate and then counted them - 10, 20, 21, 22, 23, 24, 25, 26. So 26 is the answer.
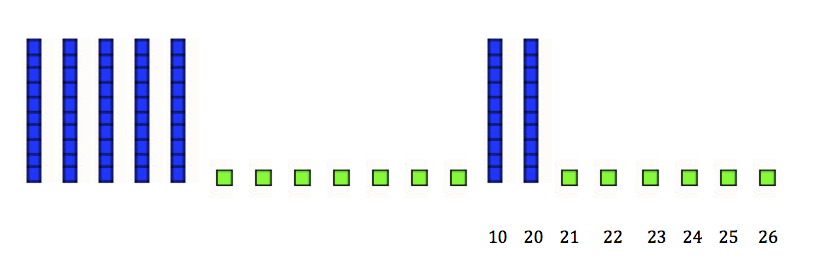
Alice: Hey - that's like what I did!
Mr. O.: What do you mean?
Alice: I didn't use blocks, but I just wrote a series of equations adding on just like Cassie did. Like this
57 + 10 = 67
67 + 10 = 77
77 + 3 = 80
80 + 3 = 83 so, 10 + 10 + 3 + 3 = 26
Mr. O.: That's a clear explanation, Alice. Cassie, would you please explain how your method and Alice's method are alike?
Cassie: Well, we both counted on by 10s as far as we could, then we added ones. I added one at a time, she added 3 at a time.
Mr. O.: Why did Alice add 3?
Cassie: I'm not sure.
Mr. O.: Alice, why did you add 3?
Alice: Because I was making a 10. 7 + 3 makes 10 and 77 ends in 7, so 77 + 3 makes 80 then I just had to add three more.
Mr. O.: Cassie, which would be more efficient - adding ones or adding 3 to make 80 and then 3 to make 83?
Cassie: Adding the 3s is faster.
Mr. O.: Making 10s can be an efficient strategy.
The next day, Mr. O. presented another problem with the same structure - different name and numbers and on a different color paper. After the class read and unpacked the story problem, Mr. O. told them to solve this problem using a different strategy than they had used the day before. If a student couldn't think of a different strategy, he/she looked at the Bansho wall to find a strategy to use. After solving the new problem, the solution strategies were added to the existing Bansho Wall.
Note: Bansho began in Japan as a way to help students learn different processes in which they can solve a problem. Bansho literally comes from the Japanese word meaning "blackboard." In math, it can be used as a way to display students' processes in solving problems.
Here is a link with a 6 minute video highlighting the Bansho strategy in a classroom. The video can be found by scrolling down to the video entitled "Bansho."
Vignette 2
Paul's Points (from 1997 MN Mathematics Framework)
In Paul's class, points are earned for completing school or homework. Tokens come in 1, 5, and 10 point values. They can all be spent at the end of each month or some can be saved for later use.
At the end of the month Paul gets 90 points in tokens. He gets nine token pieces worth 10 points each which can be traded to purchase items he wants at the school store or used to participate in a special event.
Paul wants to take the special field trip to the zoo this month which takes 25 token points. He also wants to buy some things at the school store.
Find at least three ways Paul can spend his tokens. Remember, he needs 25 token points for the field trip to the zoo.

Paul wants to be able to buy a school T-shirt within 3 months. He wants to earn it by doing extra projects without using his regular classroom points. He can pick from these extra assignments:
25 points: bring in examples of symmetry in nature (topic varies)
50 points: participate in after-school computer lab; participate in Parent Night
100 points: make a scrapbook collection (topic varies); participate in Saturday math scavenger hunt
What are some combinations of activities that would earn Paul the number of points he needs for the T-shirt?
- This activity presents a problem in context with various possible solutions. Problems like this one can be used with children throughout the primary experience by changing the values and/or the context. Instead of points, money values may be used when another context for using number sense is desired.
- Questioning and discussion is vital. "Why did you choose?" "What if...?" "How do you know?"
"What did you do about the points he would need for the field trip?"
"Did you have Paul make any long-range plans to buy the more costly items?"
- Children could illustrate their solutions as a way of recording and visualizing solutions.
Encourage verbalization of number concepts and give students the opportunity to justify the reasonableness of their solution by asking group members to share their solutions.
Where do we go from here?
Children could work together to discuss and design a savings plan to help Paul save up for a school T-shirt or jacket. Discussion could include such things as how long it might take if he saved the same number of points each month; whether 90 points was "average" and how he might earn more points. Groups could discuss and compare their various plans.
Additional Instructional Resources
Burns, Marilyn. (2007). About teaching mathematics: a k-8 resource (3rd edition). Sausalito, CA: Math Solutions Publications.
Conklin, M. (2010). It makes sense! using ten-frames to build number sense, grades k-2, Sausalito, CA: Math Solutions.
Parrish, S. (2010). Number talks: helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Small, M. (2009). Good questions: great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: teaching developmentally. (7th ed.) Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
Resources
- Students may need support in further development of previously studied concepts and skills.
- Second graders need to approach and solve problems in a way that makes sense to them, rather than just following a set of steps that may or may not make sense to them.
- While the idea of teaching "key words" might be appealing it does not support student comprehension of word problems and can lead to incorrect solutions. Another approach might be "story problem theater." When students listen to a story problem and "act out" what is happening in the problem, it is easier to see what mathematics might be involved
- Strategies second graders may use to add and subtract include the following:
- partial sums - starting on the left, with the largest place value, add the tens to get a partial sum, add the ones to get another partial sum, then add the partial sums together.
45
+37
70 (add the tens 40 + 30)
+12 (add the ones 5 + 7)
82 (add the partial sums 70 + 12)
Students might break number into tens and ones first and then add.
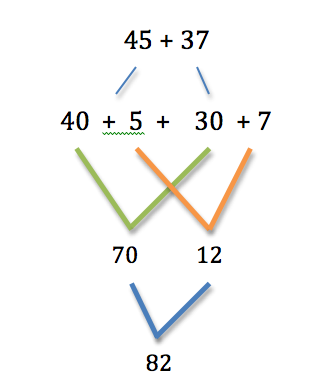
- partial differences - starting on the left, with the largest place value, subtract the tens to get a partial difference, subtract the ones to get another partial difference, then ADD the partial differences together.
58
- 17
40 (subtract the tens 50 - 10)
1 (subtract the ones 8 - 7)
41 (ADD the partial differences 40 + 1)
When any digits in the subtrahend (number being subtracted) are larger than corresponding digits in the minuend (number being subtracted from) the result will be a negative number. You can have the children discover this by having them count back on a number line that includes negative numbers
55
- 17
40 (subtract the tens 50 - 10)
-2 (subtract the ones 5 - 7 = -2)
38 (add the partial differences 40+(-2)=38)
- Using an empty number line, a visual tool that children use to keep track of their thinking as they add or subtract. For addition, put one of the addends at the beginning of the empty number line, decompose the other addend into chunks that are easy to work with based on the numbers in the problem. In this example, adding 5 to 45 to get to a multiple of 10. Then adding on multiples of 10. Keep track of the moves made above the arcs showing the jumps. Some children will be able to take a jump of 30 to get from 50 to 80. Other children may start with 45, take a jump of 30 to 75, then add 5 to get to 80.
45 + 35 =
+5 +10 +10 +10
![]()
45 50 60 70 80
For subtraction, put the minuend (the number being subtracted) at the left end of the number line. Put the subtrahend (the number being subtracted from) at the right end. This is a convention, because the value of the numbers on a number line increase as we move from left to right. 82 - 45 start with 45 + 5 → 50 + 10 → 60 + 10 →70 + 10 →80 + 2 →82
The difference between 82 and 45 is found by adding all the jumps from 45 to 82: 5 + 10 + 10 + 10 + 2 = 37
+5 +10 +10 +10 +2

45 50 60 70 80 82
- Subtract by counting up or adding on -
Can be done with or without the empty number line.
Start with the minuend (the number being subtracted - usually the smaller number). Add chunks to make "friendly" numbers.
82 - 45
45 + 5 = 50 45 + 5 = 50
50 + 10 = 60 50 + 30 = 80
60 + 10 = 70 80 + 2 = 82
70 + 10 = 80
80 + 2 = 82 45 + 5 = 50
50 + 32 = 82
Then combine all the chunks you added: 5 + 10 + 10 + 10 + 2 = 37
or 5 + 30 + 2 = 37 or 5 + 32 = 37.
The fewer steps a child uses usually indicates more efficiency.
- Using model drawing - visual tool used to help children unpack and set up many different kinds of story problems. For addition:
![]() ?
?
45 35
First you draw a bar to represent the first addend. Adjacent to that bar, draw another to represent the second addend. This is used to help the children understand what the problem is asking, it does not prescribe the solution methods. This model drawing shows the children that we are looking for the total of the two pieces of the bar, implying addition. The children write a number model to match the problem 45 + 35 = n and then they can solve it in a way that works for them.
- Compensation - in this strategy children change the numbers to make them easier to work with. Compensation is done differently for addition and subtraction.
Addition
37 + 45: Change 37 to 40 by taking 3 from the 45 and "giving it" to the 37, then add the remaining 42: revised problem 40 + 42 = 82
The important thing to remember when using compensation with addition is that when changing one number, the change has to come out of the other number, because you are working with a certain total. Think of it as a pile of 37 objects and a pile of 45 objects. To make the 37 into 40, you have to take three from the 45, leaving 42, in order to maintain the same total of objects. We are doing an "opposite change."
Subtraction
82 - 65: We want the subtrahend to be a multiple of 10, so add 5 to both numbers, then subtract: revised problem 87 - 70 =17.
With subtraction we are doing "same change" with the numbers. We
do this because with subtraction we need to maintain the same difference, or distance on a number line, so we make the same change to both numbers.
- Left to Right Addition and Subtraction
In this method the top number (addend in addition, minuend in subtraction) is left whole, and computation is started on the left, moving through the places to the right. Numbers are decomposed as necessary to make the numbers easier to add or subtract.
63 63
+ 37 - 37
93 (add 63 + 30) 33 (63 - 30)
7 (add the 7 from 37) - 3 (break the 7 into 3 and4)
100 30
- 4 (then subtract the 4)
- Not every student will invent their own strategy. Strategies can be invented by the whole class, individuals, small groups, or even introduced by the teacher. Strategies need to be shared and tried out. Students should not use a strategy without understanding it.
- Number Talks are a great way to keep strategies visible in the classroom. During a Number Talk, students are given three to five problems related to a specific strategy or problem.
Adding up is the focus of this set of problems.
|
30 - 25 30 - 24 30 - 22 30 - 21 |
Compensation is the focus of this set of problems.
|
37 + 38 38 + 26 47 + 28 33 + 38
|
- Story Problems
Second graders need exposure to different types of story problems. These types are related to work done in the Algebra Strand in first grade and continue in second grade. Second grade students should experience the following types of problems (based on the work of Carpenter, 1999, p.12). The equations describe the problem structure and may not be the equation used to find the solution.
Combining and separating problems involve an action and are easily demonstrated by second graders. Result unknown is the most common and the easiest to solve. It is important that students experience problems involving change unknown and start unknown. Of these, start unknown is the most challenging and rarely seen in second grade classrooms.
Combining
|
Result Unknown |
Lizett had 59 rocks in her collection. She found 24 rocks by the lake. How many rocks does she have now?
59 + 24 = ___ |
|
Change Unknown |
Lizett had 59 rocks in her collection. She found some more by the lake. Now she has 83 rocks. How many rocks did she find by the lake?
59 + ___ = 83 |
|
Start Unknown |
Lizett had some rocks in her collection. She found 24 more by the lake and she now has 83 rocks. How many rocks were in her collection in the beginning? ___ + 24 = 83 |
Separating
|
Result Unknown |
Lizett had 83 rocks in her collection. She lost 24 of them. How many rocks does she have now?
83 - 24 = ___
|
|
Change Unknown |
Lizett had 83 rocks in her collection. She lost some of them on the way to school. Now she has 59 rocks. How many rocks did she lose?
83 - ___ = 59
|
|
Start Unknown |
Lizett had some rocks in her collection. On the way to school she lost 24 of them. Now she has 59 rocks. How many rocks did she have in the beginning?
___ - 24 = 59
|
Part-Part-Whole problems do not involve an action. They cannot be acted out or demonstrated. The equations describe the problem structure and may not be the equation used to find the solution. The location of the unknown in part-part-whole problems can change as well.
Part-Part-Whole
|
Whole Unknown |
Lizett has 59 polished agates and 24 quartz crystals in her rock collection. How many rocks does she have in her collection?
59 + 24 = ___
|
|
Part Unknown |
Lizett has 83 rocks in her collection. 59 of them are polished agates. The rest are quartz crystals. How many quartz crystals does she have?
59 + ___ = 83
|
Comparing problems do not involve any action. Nothing is being gained or lost. Two amounts are being compared in order to find the difference or the difference is given with one amount and students are asked to find the other amount. Students may choose to add or subtract when finding an answer.
Comparing
|
Difference Unknown |
Lizett has 54 polished agates and 29 quartz crystals. How many more polished agates than quartz crystals? |
|
Compare Quantity Unknown
|
Lizett has 29 quartz crystals. She has 25 more polished agates than quartz crystals. How many polished agates does she have? |
|
Referent Unknown |
Lizett has 54 polished agates. She has 25 more polished agates than quartz crystals. How many quartz crystals does she have? |
Help children develop flexible, efficient and accurate problem solving and computational strategies. In order to be flexible and efficient, children need to develop a variety of strategies available for their use in problem solving. Strategies that second graders develop and use involve taking apart and combining numbers in a variety of ways. Most partitioning is based on making "friendly" numbers like multiples of 10, 25, and 100. Some of the common strategies are decomposition, expanded notation, left to right addition/subtraction (432 + 179; leave 432 whole, decompose the 179 into "friendly" parts of 100, 70, 8, and 1. 432 + 100 = 532, 532 + 70 = 602, 602 + 8 = 610, 610 + 1 = 611) and partial sums (432 + 179; add the hundreds first 400 + 100 = 500. Then add the tens 30 + 70 = 100. Then add the ones 9 + 2 = 11. Finally, add the "partial sums" of 500 + 100 + 11 = 611) and differences. Children tend to start on the left (with the biggest value) when they develop their own strategies for adding and subtracting. In order to use a variety of strategies, those strategies have to be understood by the children. They need to have an understanding of the operations and properties of addition and subtraction and how the operations are related. Children's use of invented strategies is usually enhanced Base10 concepts. They tend to make fewer errors when they use an algorithm they have constructed. Invented strategies enhance estimation and mental computation. We want our children to be able to select and apply appropriate computation strategies depending on the problem context and numbers involved. When children develop strategies they are more likely to understand why the procedures work.
A major stumbling block in the development of number sense skills is rushing students' use of standard algorithms to perform operations. Students quickly fixate on these methods because they can be "executed without having to think" (McIntosh et al., 1992, p. 3). We need to turn an awareness of number into an understanding of number. We need to move more thoughtfully from a conceptual understanding of operation to the development of informal algorithms. (From the Minnesota K-12 Mathematics Frameworks, 1997, Number Sense Reflections pp. 4-5.)
A common misconception regarding multi-digit addition and subtraction is that the traditional algorithms (with "borrowing" and "carrying") are the most efficient strategies and the children should be taught them right away. There is not a single strategy that is "the most efficient" strategy for every situation. Please read the excerpt from Constance Kamii and her research regarding the early introduction of standard algorithms in the section.
- Why Are Algorithms Harmful?
Algorithms are harmful to most young children for two reasons: (1) They encourage children to give up their own thinking, and (2) they "unteach" what children know about place value, thereby preventing them from developing number sense. As early as 1985, Madell (1985) made the following statement based on research he conducted in a private school in New York City: When children are allowed to do their own thinking, "they universally proceed from left to right (p. 21)." To do 36 + 46, for example, children naturally add 30 + 40 = 70 first, then 6 + 6 = 12, and finally 70 + 12 = 82. If they are taught to use the conventional U. S. algorithm, they add from right to left, which goes counter to their natural thinking. Children thus give up their own thinking, and because they have given up their own thinking, these children are not bothered by getting answers like 29 for 7 + 52 + 186. The conventional algorithm makes children treat every column as a column of ones. For example, if we listen to them while they are using the algorithm to solve
136
+246
we can hear them saying "Six and six is twelve. Put down the two and carry the one. One and three and four is eight. . . One and two is three. . . ." Treating every column as a column of ones is convenient for adults, who already know solidly that the "3" in "136" means 30. For young children who are still trying to learn place value, however, the conventional algorithms serve to "unteach" place value. ("The Harmful Effects of Algorithms in Grades 1-4" can be found in Chapter 17 of the l998 NCTM Yearbook (Kamii & Dominick, 1998).
- Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if...?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to...?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work? Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part ...
(Adapted from They're Counting on Us, California Mathematics Council, 1995)
"Vocabulary literally is the key tool for thinking."
Ruby Payne
New Vocabulary
addend: a number added to another number In 52 + 45 = 97, 52 and 45 are addends.
algorithm: step-by-step procedure for solving a problem
associative property of addition: when adding three or more addends, the way the numbers are grouped will not change the sum. For example, (7 + 8) + 2 has the same sum as 7 + (8 + 2) which is "easier" to add, because 8 + 2 = 10 and then adding 7 to 10)
commutative property of addition: when adding two numbers, changing the order of the numbers does not change the sum. For example, (4 + 9 = 9 + 4)
decomposition: breaking numbers apart into useful chunks. For example, (8 + 5, break 8 into 5 + 3 because 5 + 5 is an "easy" fact that makes 10, and then add 3 to 10 to get 13)
equation: a mathematical number sentence that has an equal sign. For example, (6 + 7 = 13, or 6 + a = 13)
expanded notation (expanded form): number written so that the value of each digit is shown. For example, (849 = 800 + 40 + 9)
expression: a mathematical phrase without any relational symbols: =, <, >, ≤, ≥, ≠, etc. For example, (2 + 3; 32 - 29; 3x, 8)
number sentence (number model): an equation or inequality using numbers, and relational symbols (=, <, >, ≤, ≥, ≠, etc.). The number sentence can include variables.
partial differences: a subtraction algorithm starting on the left and subtracting according to place value, writing down each partial difference, then combining the partial differences to get the answer:
partial sums: starting on the left, with the largest place value, add the tens to get a partial sum, add the ones to get another partial sum, then add the partial sums together.
Mathematics vocabulary words describe mathematical relationships and concepts and cannot be understood by simply practicing definitions. Students need to have experiences communicating ideas using these words to explain, support, and justify their thinking.
Learning vocabulary in the mathematics classroom is contingent upon the following:
Integration: Connecting new vocabulary to prior knowledge and previously learned vocabulary. The brain seeks connections and ways to make meaning which occurs when accessing prior knowledge.
Repetition: Using the word or concept many times during the learning process and connecting the word or concept with its meaning. The role of the teacher is to provide experiences that will guarantee connections are made between mathematical concepts, relationships, and corresponding vocabulary words.
Meaningful Use: Multiple and varied opportunities to use the words in context. These opportunities occur when students explain their thinking, ask clarifying questions, write about mathematics, and think aloud when solving problems. Teachers should be constantly probing student thinking in order to determine if students are connecting mathematics concepts and relationships with appropriate mathematics vocabulary.
Strategies for vocabulary development
Students do not learn vocabulary words by memorizing and practicing definitions. The following strategies keep vocabulary visible and accessible during instruction.
Mathematics Word Bank: Each unit of study should have word banks visible during instruction. Words and corresponding definitions are added to the word bank as the need arises. Students refer to word banks when communicating mathematical ideas which leads to greater understanding and application of words in context.

Labeled pictures and charts: Diagrams that are labeled provide opportunities for students to anchor their thinking as they develop conceptual understanding and increase opportunities for student learning.
Frayer Model: The Frayer Model connects words, definitions, examples and non-examples.
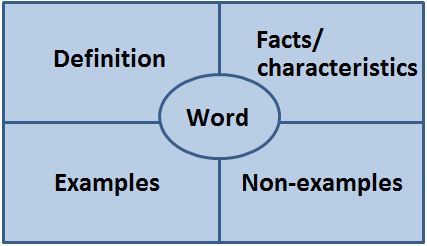
Example/Non-example Charts: This graphic organizer allows students to reason about mathematical relationships as they develop conceptual understanding of mathematics vocabulary words. Teachers should use these during the instructional process to engage student in thinking about the meaning of words.

Vocabulary Strips: Vocabulary strips give students a way to organize critical information about mathematics vocabulary words.
|
word |
definition |
illustration |
Encouraging students to verbalize thinking by drawing, talking, and writing increases opportunities to use the mathematics vocabulary words in context.
Additional Resources for Vocabulary Development
Murray, M. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Sammons, L. (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
What are the key ideas related to addition and subtraction of two two-digit numbers at the second grade level? How do student misconceptions interfere with addition and subtraction of two two-digit numbers?
What experiences do students need in order to develop an understanding of basic addition facts and the related subtraction facts?
What strategies might students have in their "math toolbox" when solving addition and subtraction problems involving two two-digit numbers?
How might a second grader solve 46 + 25 or 74 - 36?
When checking for student understanding of a strategy used in addition or subtraction of two two-digit numbers, what should teachers
- listen for in student conversations?
- look for in student work?
- ask during classroom discussions?
Examine student work related to a task involving addition or subtraction of two two-digit numbers in problem solving. What evidence do you need to say a student is proficient? Using three pieces of student work, determine what student understanding is observed through the work.
How can teachers assess student learning related to these benchmarks?
How are these benchmarks related to other benchmarks at the second grade level?
Professional Learning Community Resources
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K.. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Caldwell, J., Karp, K., Bay-Williams, J., Rathmell, E., & Zbiek, R. (2011). Developing essential understanding of addition and subtraction for teaching mathematics in prekindergarten-grade 2. Reston, VA: National Council of Teachers of Mathematics.
Carpenter, T., Fennema, E., Franke, M., Levi, L., & Empson, S.. (1999). Children's mathematics cognitively guided instruction. Portsmouth, NH: Heinemann.
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach, grades k-8, 2nd edition. Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Fosnot, C., & Dolk, M. (2001). Young mathematicians at work: Constructing number sense, addition, and subtraction. Portsmouth, NH: Heinemann.
Fuson, K., Clements, D., & Beckmann, S.. (2009). Focus in grade 2: Teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, Arthur. (2006) Comprehending math: Adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Kamii, C. & Joseph, L. (2003). Young Children Continue to Reinvent Arithmetic: 2nd Grade. New York: Teachers College Press.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Murray, M.. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Bamberger, H., Oberdorf, C., & Schultz-Ferrell, K.. (2010). Math misconceptions prek-grade 5: From misunderstanding to deep understanding. Portsmouth, NH: Heinemann.
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms!. Thousand Oaks, CA.: Corwin Press.
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting english language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Burns, M. (2007). About teaching mathematics: A K-8 Resource (3rd Edition). Sausalito, CA: Math Solutions Publications.
Burns, M. (Edt).(1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach, grades k-8, 2nd edition. Sausalito, CA: Math Solutions Press.
Chapin, S., O'Connor, C., & Canavan Anderson, N. (2009). Classroom discussions: Using math talk to help students learn (Grades K-6). Sausalito, CA: Math Solutions.
Conklin, M. (2010). It makes sense! Using ten-frames to build number sense, grades k-2, Sausalito, CA: Math Solutions Press.
Dacey, L., & Salemi, R. (2007). Math for all: Differentiating instruction k-2. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC.: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Fosnot, Catherine., Dolk, Maarten. (2001). Young mathematicians at work: Constructing number sense, addition, and subtraction. Portsmouth, NH: Heinemann.
Fuson, K., Clements, D., & Beckmann, S.. (2009). Focus in grade 2 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics.
Hyde, Arthur. (2006) Comprehending math: Adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Kamii, C. & Joseph, L. (2003). Young children continue to reinvent arithmetic: 2nd grade. New York: Teachers College Press.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC.: National Academies Press.
Leinwand, S., (2000). Sensible mathematics: a guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: transforming research for elementary school teachers. Reston, VA: National Council of Teachers of Mathematics.
Murray, M.. (2004). Teaching mathematics vocabulary in context. Portsmouth, NH: Heinemann.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom-a guide for teachers k-8. Portsmouth, NH: Heinemann.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Parrish, S. (2010). Number talks: helping children build mental math and computation strategies grades K-5. Sausalito. CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension-using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
Schielack, J., Charles, R., Clements, D., Duckett, P., Fennell, F., Lewandowski, S., Trevino, E., & Zbiek, R. M., (2006). Curriculum focal points for prekindergarten through grade 8 mathematics: a quest for coherence. Reston, VA: NCTM.
Seeley, C. (2009). Faster isn't smarter-messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Sheffield, L. J., Cavanagh, M., Dacey, L., Findell, C., Greenes, C. E., & Small, M. (2002). Navigating through data analysis and probability in prekindergarten - grade 2. Reston, VA: National Council of Teachers of Mathematics.
Small, M. (September, 2010). Beyond one right answer. Educational Leadership, 60 (1). p. 29 - 32.
Small, M. (2009). Good questions: great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Van de Walle, J., Karp, K., Bay-Williams, J. (2010). Elementary and middle school mathematics: teaching developmentally. (7th ed.) Boston, MA: Allyn & Bacon.
Van de Walle, J. & Lovin, L. (2006). Teaching student-centered mathematics grades k-3. Boston, MA: Pearson Education.
West, L., & Staub, F. (2003). Content focused coaching: transforming mathematics lessons. Portsmouth, NH: Heinemann.
Assessment
- Raul is reading a book with 83 pages. He has already read 27 pages. How many more pages does he need to read to finish the book?
Solution: 56
Benchmark: 2.1.2.4 and 2.1.2.5
- Sylvia had 37 markers. She bought 24 more.
How many markers does she have now?
a. 13
b. 61
c. 151
d. 511
Solution: b. 61
Benchmark: 2.1.2.4 and 2.1.2.5
- Make an estimate for each problem. Explain how you choose the numbers you used in your estimate.
a) 34 + 67
b) 58 + 41
c) 35 + 74
Solution: Student makes an appropriate estimate.
Benchmark: 2.1.2.3
Differentiation
Emergent learners need help understanding the structure of a problem, the information found in the problem and the question they are asked to answer.
Emergent learners will most likely begin using base ten blocks as a strategy to model the problem. They will need help connecting the materials to numbers and equations used in finding an answer.
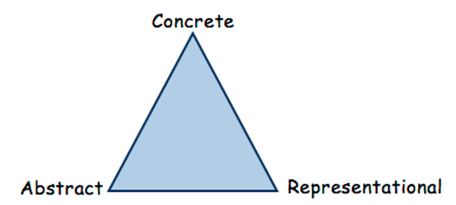
Concrete - Representational - Abstract Instructional Approach
The Concrete-Representational-Abstract Instructional Approach (CRA) is a research-based instructional strategy that has proven effective in enhancing the mathematics performance of students who struggle with mathematics.
The CRA approach is based on three stages during the learning process:
Concrete - Representational - Abstract
The Concrete Stage is the doing stage. The concrete stage is the most critical in terms of developing conceptual understanding of mathematical skills and concepts. At this stage, teachers use manipulatives to model mathematical concepts. The physical act of touching and moving manipulatives enables students to experience the mathematical concept at a concrete level. Research shows that students who use concrete materials develop more precise and comprehensive mental representations, understand and apply mathematical concepts, and are more motivated and on-task. Manipulatives must be selected based upon connections to the mathematical concept and the students' developmental level.
The Representational Stage is the drawing stage. Mathematical concepts are represented using pictures or drawings of the manipulatives previously used at the Concrete Stage. Students move to this level after they have successfully used concrete materials to demonstrate conceptual understanding and solve problems. They are moving from a concrete level of understanding toward an abstract level of understanding when drawing or using pictures to represent their thinking. Students continue exploring the mathematical concept at this level while teachers are asking questions to elicit student thinking and understanding.
The Abstract Stage is the symbolic stage. Teachers model mathematical concepts using numbers and mathematical symbols. Operation symbols are used to represent addition, subtraction, multiplication and division. Some students may not make a clean transfer to this level. They will work with some symbols and some pictures as they build abstract understanding. Moving to the abstract level too quickly causes many student errors. Practice at the abstract level will not lead to increased understanding unless students have a foundation based upon concrete and pictorial representations.
- Language and vocabulary are stumbling blocks when English Language Learners are asked to solve a problem in context. Problematic vocabulary may include sum, compare, take away, fewer, more, difference, addition, subtraction,
- Word banks need to be part of the student learning environment in every mathematics unit of study.
- Use vocabulary graphic organizers such as the Frayer model (see below) to emphasize vocabulary words count, first, second, third, etc.

- Sentence Frames
Math sentence frames provide support that English Language Learners need in order to fully participate in math discussions. Sentence frames provide appropriate sentence structure models, increase the likelihood of responses using content vocabulary, help students to conceptualize words and build confidence in English Language Learners.
Sample sentence frames related to these benchmarks:
|
I used the __________ strategy to solve the problem. First I ________ then _______. |
|
This problem is asking us to find _____________________________________________. |
When assessing the math skills of an ELL student it is important to determine if the student has difficulty with the math concept or with the language used to describe the concept and conceptual understanding.
Additional ELL Resources:
Bresser, R., Melanese, K., & Sphar, C. (2008). Supporting English language learners in math class, grades k-2. Sausalito, CA: Math Solutions Publications.
Using a variety of strategies requires a solid understanding of operations and properties of numbers. Facilitate the discovery of patterns and relationships between strategies. Encourage students to solve a problem using a specific strategy.
Additional Resources
Bender, W. (2009). Differentiating math instruction: Strategies that work for k-8 classrooms! Thousand Oaks, CA.: Corwin Press.
Dacey, L., & Lynch, J. (2007). Math for all: Differentiating instruction grades k-2. Sausalito, CA: Math Solutions.
Murray, M. & Jorgensen, J. (2007). The differentiated math classroom: A guide for teachers k-8. Portsmouth, NH: Heinemann.
Small, M. (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
Parents/Admin
|
Students are... |
Teachers are... |
|
adding and subtracting a variety of numbers |
differentiating learning experiences to meet student needs. Using open questions, visuals for vocabulary, or additional guidance are a few ideas. |
|
composing and decomposing numbers to aid in calculations. for example, when solving 68 + 24, it helps to decompose the addends to 68 + 2 + 22 and then recompose as 70 + 22 = 92. |
providing appropriate manipulatives such as using base-ten blocks for student use. |
|
checking their answers for reasonableness by reflecting on the numbers. |
evaluating student strategies/reasoning for mathematical accuracy. |
|
talking about mathematics . |
establishing a learning environment that values student ideas, |
|
sharing, comparing, and contrasting their strategies for adding and subtracting two-digit numbers. |
facilitating classroom discussions about strategies and relationships between numbers. |
|
solving different types of real-world story problems. |
providing varied real-world contexts problem solving,
|
Additional Resources
For Mathematics Coaches
Chapin, S. and Johnson, A. (2006). Math matters: Understanding the math you teach: Grades k-8, 2nd edition. Sausalito, CA: Math Solutions.
Donovan, S., & Bradford, J. (Eds). (2005). How students learn: Mathematics in the classroom. Washington, DC: National Academies Press.
Felux, C., & Snowdy, P. (Eds.). ( 2006). The math coach field guide: Charting your course. Sausalito, CA: Math Solutions.
Sammons, L., (2011). Building mathematical comprehension: Using literacy strategies to make meaning. Huntington Beach, CA: Shell Education.
West, L., & Staub, F. (2003). Content focused coaching: Transforming mathematics lessons. Portsmouth, NH: Heinemann.
For Administrators
Burns, M. (Ed). (1998). Leading the way: Principals and superintendents look at math instruction. Sausalito, CA: Math Solutions.
Kilpatrick, J., & Swafford, J. (Eds). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.
Leinwand, S. (2000). Sensible mathematics: A guide for school leaders. Portsmouth, NH: Heinemann.
Lester, F. (2010). Teaching and learning mathematics: Transforming research for school administrators. Reston, VA: National Council of Teachers of Mathematics.
Seeley, C. (2009). Faster isn't smarter: Messages about math teaching and learning in the 21st century. Sausalito, CA: Math Solutions.
Mathematics handbooks to be used as home references:
Cavanagh, M. (2004). Math to Know: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Cavanagh, M. (2006). Math to learn: A mathematics handbook. Wilmington, MA: Great Source Education Group, Inc.
Helping your child learn mathematics
Provides activities for children in preschool through grade 5
What should I look for in the mathematics program in my child's school? A Guide for Parents developed by SciMathMN
Help Your Children Make Sense of Math
Ask the right questions
In helping children learn, one goal is to assist children in becoming critical and independent thinkers. You can help by asking questions that guide, without telling them what to do.
Good questions, and good listening, will help children make sense of the mathematics, build self-confidence and encourage mathematical thinking and communication. A good question opens up a problem and supports different ways of thinking about it. The best questions are those that cannot be answered with a "yes" or a "no."
Getting Started
What do you need to find out?
What do you know now? How can you get the information? Where can you begin?
What terms do you understand/not understand?
What similar problems have you solved that would help?
While Working
How can you organize the information?
Can you make a drawing (model) to explain your thinking? What are other possibilities?
What would happen if . . . ?
Can you describe an approach (strategy) you can use to solve this?
What do you need to do next?
Do you see any patterns or relationships that will help you solve this?
How does this relate to ...?
Can you make a prediction?
Why did you...?
What assumptions are you making?
Reflecting about the Solution
How do you know your solution (conclusion) is reasonable? How did you arrive at your answer?
How can you convince me your answer makes sense?
What did you try that did not work?
Has the question been answered?
Can the explanation be made clearer?
Responding (helps clarify and extend their thinking)
Tell me more.
Can you explain it in a different way?
Is there another possibility or strategy that would work?
Is there a more efficient strategy?
Help me understand this part...
Adapted from They're counting on us, California Mathematics Council, 1995
Create opportunities to engage your child in math frequently. Your child might use estimation skills to decide if a package of 40 candy bars is enough for everyone in their class to have two for their birthday. Then, your child could use a calculator or pencil and paper to check their answer. Making up humorous stories about adding and subtracting would be great practice. For example, I had 55 candy pieces and my brother took zero. How many did I have left? Share your math thinking as you work through a mathematical opportunity. You might be considering the best value for your money at the grocery store or how many buns to purchase for a party.
Playing the game of "Target 50" creates a fun opportunity to reinforce adding two-digit numbers. Take turns entering a two-digit number on a calculator and the other person must add a number that will get as close as possible to 50.
Websites
- This link provides a game to practice estimating sums and differences up to 100
- Here is a link to real-world addition word problems
- Here is a link to real-world subtraction word problems:
