6.1.2 Ratios & Rates
Identify and use ratios to compare quantities; understand that comparing quantities using ratios is not the same as comparing quantities using subtraction.
For example: In a classroom with 15 boys and 10 girls, compare the numbers by subtracting (there are 5 more boys than girls) or by dividing (there are 1.5 times as many boys as girls). The comparison using division may be expressed as a ratio of boys to girls (3 to 2 or 3:2 or 1.5 to 1).
Apply the relationship between ratios, equivalent fractions and percents to solve problems in various contexts, including those involving mixtures and concentrations.
For example: If 5 cups of trail mix contains 2 cups of raisins, the ratio of raisins to trail mix is 2 to 5. This ratio corresponds to the fact that the raisins are $\frac{2}{5}$ of the total, or 40% of the total. And if one trail mix consists of 2 parts peanuts to 3 parts raisins, and another consists of 4 parts peanuts to 8 parts raisins, then the first mixture has a higher concentration of peanuts.
Determine the rate for ratios of quantities with different units.
For example: 60 miles for every 3 hours is equivalent to 20 miles for every one hour (20 mph).
Use reasoning about multiplication and division to solve ratio and rate problems.
For example: If 5 items cost \$3.75, and all items are the same price, then 1 item costs 75 cents, so 12 items cost \$9.00.
Overview
Standard 6.1 2 Essential Understandings
The concept of ratio is a critical foundation in the learning progression of algebra concepts, connecting rational numbers to proportion to function in future years. Students at this level use simple reasoning about multiplication and division to solve ratio and rate problems. For example, If 5 items costs $3.75 and all items are the same price, then the cost of 12 items can be found by first dividing $3.75 by 5 to find the cost of one item and then multiplying the cost of a single item by 12. By analyzing simple drawings that indicate relative size of quantities and viewing equivalent ratios and rates as deriving from, and extending, pairs of rows (or columns) in the multiplication table, students extend whole number multiplication and division to ratios and rates. Thus, they expand the repertoire of problems that they can solve by multiplication and division, and build on their understanding of fractions to understand ratios. Students apply their knowledge of ratios, equivalent fractions, and percents to solve a wide variety of problems, including those involving mixtures and concentrations.
All Standard Benchmarks
6.1.2.1 Identify and use ratios to compare quantities; understand that comparing quantities using ratios is not the same as comparing quantities using subtraction.
6.1.2.2 Apply the relationship between ratios, equivalent fractions and percents to solve problems in various contexts, including those involving mixtures and concentrations.
6.1.2.3 Determine the rate for ratios of quantities with different units.
6.1.2.4 Use reasoning about multiplication and division to solve ratio and rate problems.
6.1.2.1 Identify and use ratios to compare quantities; understand that comparing quantities using ratios is not the same as comparing quantities using subtraction.
6.1.2.2 Apply the relationship between ratios, equivalent fractions and percents to solve problems in various contexts, including those involving mixtures and concentrations.
6.1.2.3 Determine the rate for ratios of quantities with different units.
6.1.2.4 Use reasoning about multiplication and division to solve ratio and rate problems.
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Understand that ratios can express part-to-part, part-to-whole, or whole-to-part relationships;
- Identify ratios in various contexts and represent them in multiple ways;
- Use reasoning about multiplication and division to determine equivalent ratios;
- Determine unit rates;
- Use the relationships between ratios, equivalent fractions, and percents to solve a variety of problems, including those involving mixtures and concentrations.
Work from previous grades that supports this new learning includes:
- Understand that a ratio is a comparison of two quantities;
- Understand that ratios can be represented in more than one way;
- Identify, order, write and compare fractions, mixed numbers, improper fractions, decimals, and percents;
- Locate fractions, mixed numbers, improper fractions, and decimals on a number line;
- Add and subtract decimals and fractions using multiple strategies including standard algorithms and a variety of representations;
- Use <, =, and > symbols to express relationships;
- Use equivalent fractions as a strategy to add and subtract unlike fractions;
- Multiply and divide whole numbers;
- Solve real-world and mathematical problems requiring addition and subtraction of decimals, fractions and mixed numbers, including those involving measurement, geometry and data.
NCTM Standards:
Understand numbers, ways of representing numbers, relationships among numbers, and number systems
- work flexibly with fractions, decimals and percents to solve problems;
- understand and use ratios and proportions to represent quantitative relationships;
Compute fluently and make reasonable estimates
- develop, analyze, and explain methods for solving problems involving proportions, such as scaling and finding equivalent ratios
Understand patterns, relations, and functions
- represent, analyze, and generalize a variety of patterns with tables, graphs, words, and, when possible, symbolic rules;
- relate and compare different forms of representation for a relationship.
Common Core State Standards (CCSS):
6RP (Ratio and Proportional Relationships) Understand ratio concepts and use ration reasoning to solve problems.
- 6RP.1 Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
- 6RP.2 Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0.
- 6RP.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios.
- 6RP.3.d Use ratio reasoning to manipulate and transform units appropriately when multiplying or dividing.
Misconceptions
Student Misconceptions and Common Errors
- Students may believe that 8:4 and 2:1 represent different ratios;
- Students may not understand that order matters in a ratio. For example, students may believe that 3:1 and 1:3 are the same ratios;
- Given the ratio 3 boys to every 7 girls, students may think there are exactly only 3 boys and 7 girls;
- Students see little difference between fractions and ratios, believing that all ratios express part-to-whole relationships;
- Students may misinterpret or misrepresent ratios expressed in words. For example, students may believe that the ratio of problems wrong to problems correct is 1:6 when a student gets one out of every six problems wrong rather than 1:5;
- Students believe that adding or subtracting the same number to the numerator and denominator produces an equivalent ratio (e.g., $\frac{4}{8}$ is equivalent to $\frac{4+2}{8+2}$ or $\frac{6}{10}$;
- When scaling up by non-integer values, students revert to additive structures (e.g., When asked, "If it takes 6 pizzas to feed 24 people, how many pizzas will it take to feed 36 people," students add 6 + 12 rather than multiply 6 x 1.5);
- Students do not understand unit rates as fractions (e.g., 25 students per bus means $\frac{25 students}{1bus}$)
Vignette
In the Classroom
In the following vignette, students begin their investigation of ratio by solving a problem with familiar context using their prior knowledge of multiplication, division, or fractions. Later, the same problem is solved using the ideas of ratios and equivalent ratios.
Class Party Problem: You are planning a menu for a class party. Each student will receive one drink at the party. Your teacher tells you that for a class this size, you can expect 3 out of 5 students to prefer cola, whereas 2 out of 5 will prefer lemonade. If, in fact, this guideline proves true for your class of 30 students, how many students will want cola? How many will want lemonade?
Teacher: How did you find the number of colas and the number of lemonades you should order?
Student: I drew a picture to represent the problem. I drew a column of 5 circles to represent the 5 students. I labeled 3 with C for cola and 2 with L for lemonade. Then I drew more of these columns of 5 circles until I had 30 circles.

Teacher: How does your model show the answer?
Student: My circles show the number of Cs (colas) and Ls (lemonades) for 30 students. There are 18 Cs and 12 Ls, so I would order 18 colas and 12 lemonades.
Teacher: That makes sense. I can see that if you have 18 colas for 30 students and 12 lemonades for 30 students, then you have 3 colas for every 5 students and 2 lemonades for every 5 students. Did anyone else use a drawing to solve the problem?
Student: I started to, but I realized that I didn't need to draw all the circles.
Teacher: Tell us why.
Student: I knew I needed 30 circles in all - that's 6 groups because there are 5 in each group. There are 3 Cs in each group, so there are 6 groups of 3 Cs, or 6 x 3 = 18 Cs in all. There are 2 Ls in each group, so there are 6 groups of 2 Ls, or 6 x 2 = 12 Ls in all. I used multiplication.
Teacher: I understand. You used division and then multiplication to make sure that there were 3 colas for every 5 students and 2 lemonades for every 5 students. You ended up with 18 colas for 30 students and 12 lemonades for 30 students.
Student: I used division and multiplication, but I didn't draw a model. I know that 30÷ 5 = 6, so there are six 5s in 30. That means that I would need 6 x 3 = 18, so I need 18 colas, and 6 x 2 = 12, so I need 12 lemonades. I added 18 + 12 = 30, so I know my answer is right.
Teacher: So you also ended up with 18 colas for 30 students and 12 lemonades for 30 students, which is also 3 colas for every 5 students and 2 lemonades for every 5 students.
Student: I drew the same picture, but I used fractions to solve the problem.

The fraction of 5 students that want cola is ⅗.The fraction of 5 students that want lemonade is ⅖. Then I used equivalent fractions to find the fraction of 30 students that want cola and lemonade.
$\frac{3}{5}=\frac{?}{30}$ $\frac{3 \times 6}{5 \times 6}=\frac{18}{30}$
So I need to order 18 colas.
$\frac{2}{5}=\frac{?}{30}$ $\frac{2 \times 6}{5 \times 6}=\frac{12}{30}$
So I need to order 12 lemonades. Add 18 + 12 = 30, so my answer is right.
Teacher: Again, there are 18 colas for 30 students (or 3 colas for every 5 students) and 12 lemonades for 30 students (or 2 lemonades for every 5 students). So what we've done today is use the idea called ratio. When we describe this situation by saying things like 3 for every 5 and 18 for every 30, we are using ratio language. We were able to use what we know about fractions and multiplication and division in this ratio situation because those ideas are also related to the idea of comparing some number to another number.
Later that week...
Teacher: Remember how we used drawings and multiplication and division to solve the Class Party Problem?
(Teacher reviews drawings and procedures.)
Now we know that we can use the ideas of ratios and equivalent ratios to solve the problem. Let's revisit the Class Party Problem, this time using ratios to compare the students who want cola and lemonade to the class, and then finding equivalent ratios for thirty students.
Sample student work:

Note: Students may understand that rather than use equivalent ratios to find both the number of colas and the number of lemonades needed for 30 students, they could find the equivalent ratio for one drink, and subtract that from the total, 30, to find the number of the other drink. For example, if students found that they needed 18 colas for 30 students, then they can surmise that they need 30 - 18, or 12, lemonades. Completing the problem both ways is valuable so that students realize that the sum of the colas and the lemonades equals 30, which is 18 + 12 = 30.
Resources
Teacher Notes
- Students that struggle to identify equivalent ratios written in the form a:b will benefit from representing the ratios with fractions before determining equivalency. For example, by writing 8:4 as $\frac{8}{4}$ and 2:1 as $\frac{2}{1}$, it quickly becomes apparent that the two ratios are equivalent. Similarly, by writing 3:1 as $\frac{3}{1}$ and 1:3 as $\frac{1}{3}$, it becomes apparent that the ratios are not equivalent and order matters;
- Visual models can help students understand that ratios represent a comparison of two quantities by division, rather than two unique quantities. The following pictures show that if the ratio of number of pieces of pizza eaten to the total number of pieces of pizza is $\frac{1}{2}$, that does not mean that the pizza was necessarily cut into 2 pieces;
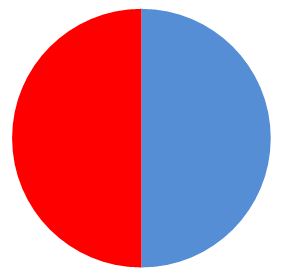
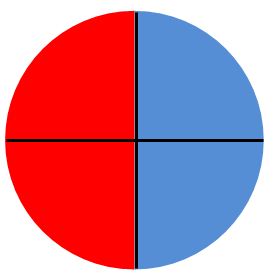
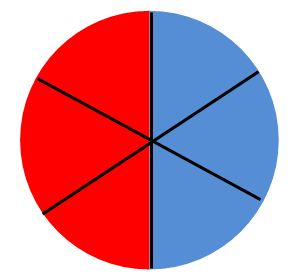
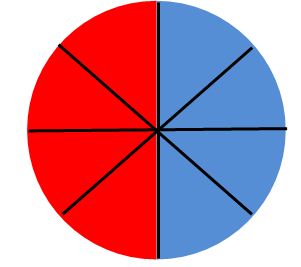
- As students begin to use what they know about fractions to make comparisons, they will learn to make other comparisons. For example, if the ratio of children to adults in a family is 4 to 2, they can compare the number of adults to the total number of people in the family with the ratio 2 to 6, and so on. In general, students will learn that they can write part-to-part, part-to-whole, and whole-to-part ratios.
- Students must pay close attention to language to determine whether they are being asked to represent a part-to-part, part-to-whole, or whole to part ratio;
- Students also need to build a connection from division to ratio and rate. This can be accomplished when they learn that a ratio is a comparison of two numbers by division; for example, the ratio 4:5 can be written as $\frac{4}{5}$ and is the quotient of 4÷5. Students will use this relationship when they write ratios as decimals.
- Before connecting multiplication and division to the concepts of ratio and rate, students first need to build a connection from additive reasoning to multiplicative reasoning. That is, they need to understand that 2 times has a different meaning than 2 more than, and so on.
- Teachers must help students make the transition from only thinking about a fraction as representing the comparison of a part to a whole to thinking about a fraction as a representation of many types of ratios. Expanding this thinking is particularly important in dealing with the difference between the representations of equivalent fractions and equivalent ratios. In common representations of equivalent fractions, the whole stays the same. To create the equivalence, the whole is divided into smaller and smaller parts.
- Teachers need to demonstrate that any fraction can be expressed in an infinite number of ways.

By contrast, in common representations of equivalent ratios, the whole is replicated over and over, or multiplied. In the equivalent ratios 1:2 = 2:4 = 3:6 = 5:10, the 1-for-every-2 relationship is replicated over and over, or multiplied, and the relationship of the new parts to the new whole does not change. This concept of scaling lays the foundation of proportionality in later grades.

- Visuals can be used to confront the misconception that adding or subtracting the same number in the numerator and denominator does not produce equivalent ratios, rather multiplying or dividing does.
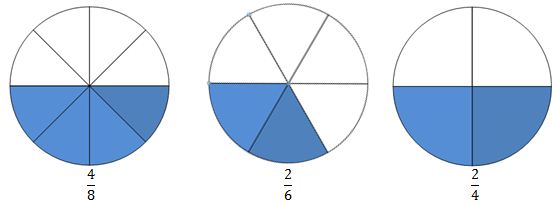
Example: $\frac{4}{8}$ is not equivalent to $\frac{4-2}{8-2}$, or $\frac{2}{6}$. However, $\frac{4}{8}$ is equivalent to $\frac{4÷2}{8÷2}$, or $\frac{2}{4}$.
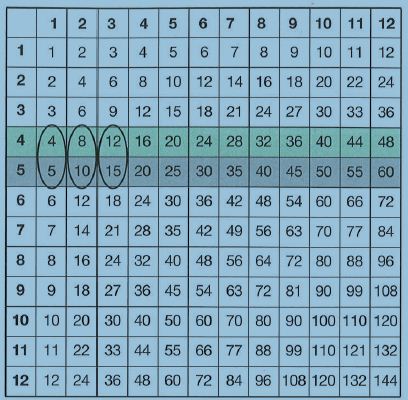
- The multiplication table is a powerful model to show equivalent fractions, and therefore, equivalent ratios. For example, following the rows for 4 and 5 to the right on the table shown below shows the equivalent ratios $\frac{4}{5}, \frac{8}{10}, \frac{12}{15},$ and so on.
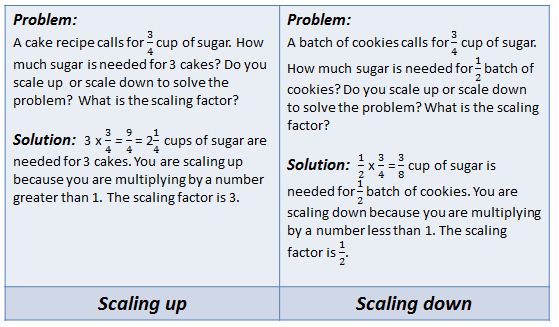
- A useful activity to help students build a connection from multiplication to ratio and rate is to explore multiplication as scaling. When a quantity is multiplied by a number greater than 1, it is scaled up. When a number is multiplied by a positive number less than 1, it is scaled down. Opportunities to examine such problems as those shown below can help students understand the concept of scaling.
● Ask students to recall when they have heard or used expressions with the word per, and make a list the expressions. Explain that these are all rates and have a denominator of 1. Ask students how they would find a unit rate from a rate such as $32.50 for 10 gallons of gas. Conversely, ask how they would use a unit rate of 25 miles per gallon to determine the number of miles traveled using 10 gallons.
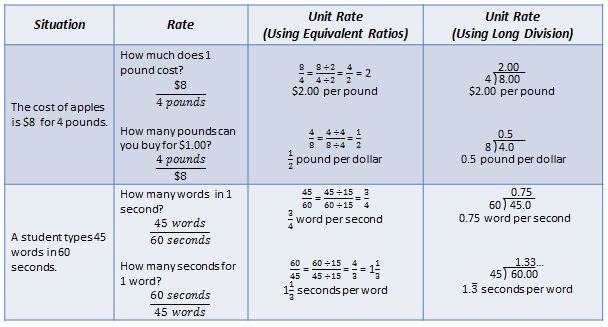
● The words used to describe unit rates (e.g., 25 students per bus), and the fact that students often see unit rates described with only one number visible, make it difficult for students to think about unit rates in fraction form. It is beneficial for students to understand that every rate situation can be written in two ways with two different unit rates, with either unit as 1. For example, the situation in which 6 pounds of bananas cost $3 can be written as the rate $\frac{6 pounds}{3 dollars}$ and as the unit rate in terms of pounds per dollar: $\frac{2 pounds}{1 dollar}$. The same situation can be described by the rate $\frac{3 dollars}{6 pounds}$ and as the unit rate in terms of dollars per pound: $\frac{0.5 dollars}{1 pound}$ or $\frac{$0.50}{1 pound}$. When the unit rate is written in terms of amount of money for 1 quantity, then it is called the unit cost or unit price. In either instance, to find the unit rate, one must find the equivalent ratio whose denominator is 1 unit. Two ways to find equivalent unit rates is to use equivalent ratios or divide the numerator by the denominator.
● Students will benefit from constructing various representations of additive relationships and multiplicative relationships, as shown below.
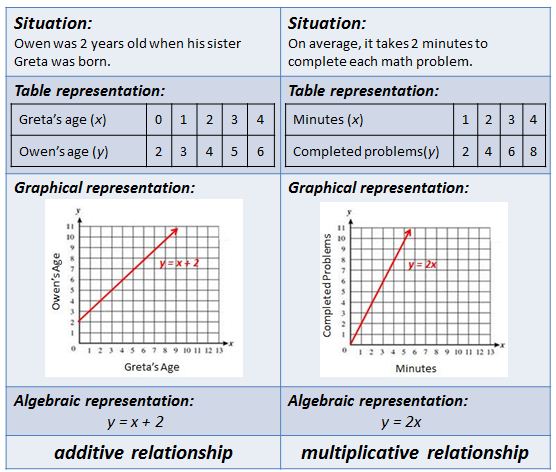
Description: By using sampling from a large collection of beans, students get a sense of equivalent fractions, which leads to a better understanding of proportions. Equivalent fractions are used to develop an understanding of proportions. This lesson can be adapted for lower-skilled students by using a more common fraction, such as $\frac{2}{3}$. It can be adapted for upper grades or higher-skilled students by using ratios that are less instinctive, such as $\frac{12}{42}$ (which reduces to $\frac{2}{7}$).
Additional Instructional Resources
● Ratio. Fraction. What's the Difference?
This lesson explains why ratios and fractions are actually two different ideas and when they can actually overlap.
per: for each, or for every; often used with units to express a rate. Example: If apples cost $1.99 per pound, then each pound of apples costs $1.99.
percent: a ratio comparing a number to 100. Example: 45% = $\frac{45}{100}$
proportion: an equation that states that two ratios are equivalent. Example: $\frac{2}{3}=\frac{4}{6}$
rate: a ratio that compares two quantities measured in different units; may be expressed using the word per. Examples: $\frac{100 students}{4 buses}$; 100 students per 4 buses.
ratio: a comparison of two quantities by division. Examples: 12 to 25, 12:25, $\frac{12}{25}$
unit rate: a rate with a denominator of 1 unit. Example: $\frac{$3.89}{1 gallon}$ or $3.89 per gallon
Reflection - Critical Questions regarding teaching and learning of these benchmarks
- How have equivalent fractions been used to build an understanding of equivalent ratios?
- Do students have enough time and experiences to fully understand ratio concepts before moving on to related proportional ideas?
- How can problem solving be used to strengthen connections among multiplication, division, fractions, and ratio?
- What experiences help students see why additive strategies don't make sense when working with ratios?
- How were real-life problems used to engage students?
- What evidence exists to show that students are transitioning from concrete and numerical representations to algebraic reasoning, generalization, and abstract representations?
Materials - suggested articles and books
Details about these materials can be found in the References section.
● NCTM. A Research Companion to Principles and Standards for School Mathematics, Chapter 14, The Ratio Concept, p. 217.
Keeley, P., & Rose, C. (2006). Mathematics curriculum topic study. Thousand Oaks, CA: Corwin Press.
Kilpatrick, J., Martin, W., & Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
Minnesota's K-12 Mathematics Frameworks. (1998). St. Paul, MN: SciMathMN.
National Council of Teachers of Mathematics. (2010). Focus in grade 6 teaching with curriculum focal points. Reston, VA: National Council of Teachers of Mathematics, Inc.
National Council of Teachers of Mathematics. (2010). Developing essential understanding of ratios, proportions & proportional reasoning grades 6-8. Reston, VA: National Council of Teachers of Mathematics, Inc.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics, Inc.
Assessment
(DOK Level 1)
- Ashley bought a twelve pack of juice boxes for $3.84. How much did one juice box cost?

a. 0.32 b. $0.40 c. $3.20 d. $4.00
Answer: a
(DOK Level 1)
2. A map uses 8 cm to represent 28 miles. How many cm would be used to represent 70 miles?
Answer: 20 cm
(DOK Level 2)
3. Sam read 60 pages of his novel in 100 minutes. How many pages of his novel can Sam expect to read in 45 minutes if he reads at the same rate?

Answer: 27 pages
(DOK Level 2)
4. Ashley biked 32 miles in 2 hours. Mike biked 12 miles in 1 hour. How much farther can Ashley bike than Mike in 5 hours if they both continue at the same rate?

a. 16 miles b. 20 miles c. 24 miles d. 28 miles
Answer: b
DOK Level 3)
5. A drink recipe calls for 1 part lemonade, 3 parts orange juice, and 4 parts water. How much lemonade, orange juice, and water are needed to make 64 fluid ounces of the drink using the recipe? Explain how you found your answer.
Answer: Sixty-four fluid ounces of the drink will require 8 fluid ounces lemonade, 24 fluid ounces orange juice, and 32 fluid ounces water.My first step was to find the total number of parts: 1 part + 3 parts + 4 parts = 8 parts.Then I divided the total number of fluid ounces by the total number of parts: $\frac{64\ fluid\ ounces}{8\ parts}=\frac{8\ fluid\ ounces}{1\ part}$. Next I multiplied the number of parts by $\frac{8\ fluid\ ounces}{1\ part}$ to find the number of fluid ounces of each ingredient:
lemonade - $1\ part \times \frac{8\ fluid\ ounces}{1\ part}=8$ fluid ounces;
orange juice - $3\ parts \times \frac{8\ fluid\ ounces}{1\ part}=24$ fluid ounces;
water - $4\ parts \times \frac{8\ fluid\ ounces}{1\ part}=32$ fluid ounces.
I know my answer is reasonable because when I add the number of fluid ounces of each ingredient, I get 64 fluid ounces: (8 fluid ounces lemonade + 24 fluid ounces orange juice + 32 fluid ounces water = 64 fluid ounces drink).
(DOK Level 3)
6. A photo measuring 4 inches wide by 6 inches long needs to be enlarged to be 8 inches wide, using the same ratio for the dimensions.

Carlos says that the new dimensions will be 8 inches wide by 10 inches long. Devon says the new dimensions will be 8 inches wide by 12 inches long. Which student is correct? Explain how you know.
Answer: Devon is correct because $\frac{4}{6}$ and $\frac{8}{12}$ are equivalent ratios.
$\frac{4}{6} \times \frac{2}{2}=\frac{4 \times 2}{6 \times 2}= \frac{8}{12}$.
(DOK Level 4)
7. Your school plans to install a new flagpole that is a minimum of 20 feet high. When flown on a flagpole, it is suggested that the width of the American flag is $\frac{1}{4}$ the height of the flagpole. The standard ratio for width: length of the American flag is 10:19. Your task is to recommend a flagpole height and flag dimensions. Justify that your recommendations meet the requirements.

Sample Answer: I recommend a 24 foot flagpole with an American flag that measures 6 feet wide: $\frac{6\ feet\ (flag\ width)}{24\ feet\ (flagpole\ height)}=\frac{1}{4}$
Differentiation
- When describing a ratio such as 2:3 to students, it may be helpful to use language such us "for every..." E.g., for every 2 parts concentrate, we need 3 parts water.
- Use pictorial representations to help students visualize ratios;
![]()
- Encourage students to look for patterning when working with a rate table.
- Continue working with a number line to show the magnitude of a fraction or ratio;
- e.g., lay out more than one number line containing differing pre-segmented parts to compare two fractions.
- Using a multiplication table can assist with showing equivalent ratios. To help students see equivalent ratios when using non-consecutive rows such as 2 and 7 to make $\frac{2}{7},\frac{4}{14},$ and $\frac{6}{21}$, have the students cut apart the rows of the table and reposition the rows so they are directly above each other.
![]()
![]()
- Teach and assist students in translating statements in word problems into mathematical expressions.
- Create a visual glossary that includes examples of ratios represented in different forms, rates, unit rates, and proportions;
- Use Venn diagrams to show relationships among ratios, rates, unit rates, and proportions;
- Use pictorial representations of word problems to assist in problem solving;
- Use graphic organizers such as the Frayer model shown below, for vocabulary development.
ConstantDimensions
In this lesson, students measure the length and width of a rectangle with standard and nonstandard units to discover that the ratio of length to width is constant.
FreeRide
In this activity, an applet allows students to vary the gear ratio of a bike. Students choose a route and attempt to capture five flags place on the route.
Capture-Recapture
In this lesson, students learn how to estimate the size of a total population by taking samples and using proportions.
Parents/Admin
Administrative/Peer Classroom Observation
|
Students are: (descriptive list) |
Teachers are: (descriptive list) |
|
identifying part-to-part, part-to-whole, and whole-to-part ratios and representing them in different forms. |
transitioning students from thinking about fractions only as part-to-whole relationships to thinking about fractions as representations for many types of ratios. |
|
using multiplication tables to explore equivalent ratios. |
making explicit connections between pairs of rows (or columns) and equivalent ratios. |
|
finding equivalent ratios. |
building on student understanding of equivalent fractions. |
|
using reasoning about multiplication and division to solve problems involving proportional relationships. |
posing problems involving proportional relationships that arise from students' real-world experiences. |
|
using numbers, tables, graphs, and equations to think about quantities and their relationships. |
pointing out the difference between additive and multiplicative relationships. |
|
representing proportional relationships in words, tables, graphs, and equations. |
asking students to use multiple representations of proportional relationships. |
|
discussing, writing, and reflecting about their reasoning. |
paying attention to student reasoning to help them transition from concrete and numerical representations to algebraic reasoning, generalization, and abstract representations. |
Parent Resources
- Ratios, a website that explains how ratios are used to build proportions.
- Ratio and Proportion, a website that includes sample worked problem
- Ratios as Fractions in Simplest Form, a video that explains how ratios written in various forms can be rewritten as fractions in simplest form.
- Simplifying Rates and Ratios, a video that uses factor trees to find common factors and simplify rates and ratios.
- Finding Unit Rates, a video that uses division to find unit rates.
